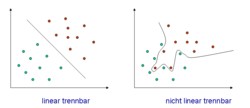
Lineare Separierbarkeit — Zwei voneinander nicht linear separierbare Relationen in … Deutsch Wikipedia
Support-Vector-Machine — Eine Support Vector Machine [səˈpɔːt ˈvektə məˈʃiːn] (SVM, die Übersetzung aus dem Englischen, „Stützvektormaschine“ oder Stützvektormethode, ist nicht gebräuchlich) ist ein Klassifikator (vgl. Klassifizierung). Eine Support Vector Machine… … Deutsch Wikipedia
Support-Vector-Maschine — Eine Support Vector Machine [səˈpɔːt ˈvektə məˈʃiːn] (SVM, die Übersetzung aus dem Englischen, „Stützvektormaschine“ oder Stützvektormethode, ist nicht gebräuchlich) ist ein Klassifikator (vgl. Klassifizierung). Eine Support Vector Machine… … Deutsch Wikipedia
Support-Vektor-Maschine — Eine Support Vector Machine [səˈpɔːt ˈvektə məˈʃiːn] (SVM, die Übersetzung aus dem Englischen, „Stützvektormaschine“ oder Stützvektormethode, ist nicht gebräuchlich) ist ein Klassifikator (vgl. Klassifizierung). Eine Support Vector Machine… … Deutsch Wikipedia
Supportvektormaschine — Eine Support Vector Machine [səˈpɔːt ˈvektə məˈʃiːn] (SVM, die Übersetzung aus dem Englischen, „Stützvektormaschine“ oder Stützvektormethode, ist nicht gebräuchlich) ist ein Klassifikator (vgl. Klassifizierung). Eine Support Vector Machine… … Deutsch Wikipedia
Support Vector Machine — Eine Support Vector Machine [səˈpɔːt ˈvektə məˈʃiːn] (SVM, die Übersetzung aus dem Englischen, „Stützvektormaschine“ oder Stützvektormethode, ist nicht gebräuchlich) ist ein Klassifikator (vgl. Klassifizierung). Eine Support Vector Machine… … Deutsch Wikipedia
FLD — Die Fisher’sche Diskriminanzfunktion ist eine Diskriminanzfunktion, die das Fisher’sche Kriterium realisiert. Dieses wurde 1936 von R. A. Fisher entwickelt und beschreibt eine Metrik, die die Güte der Trennbarkeit zweier Klassen in einem… … Deutsch Wikipedia
Fisher'sche Diskriminanzfunktion — Die Fisher’sche Diskriminanzfunktion ist eine Diskriminanzfunktion, die das Fisher’sche Kriterium realisiert. Dieses wurde 1936 von R. A. Fisher entwickelt und beschreibt eine Metrik, die die Güte der Trennbarkeit zweier Klassen in einem… … Deutsch Wikipedia
Fishersche Diskriminante — Die Fisher’sche Diskriminanzfunktion ist eine Diskriminanzfunktion, die das Fisher’sche Kriterium realisiert. Dieses wurde 1936 von R. A. Fisher entwickelt und beschreibt eine Metrik, die die Güte der Trennbarkeit zweier Klassen in einem… … Deutsch Wikipedia
Fishersche Diskriminanzfunktion — Die Fisher’sche Diskriminanzfunktion ist eine Diskriminanzfunktion, die das Fisher’sche Kriterium realisiert. Dieses wurde 1936 von R. A. Fisher entwickelt und beschreibt eine Metrik, die die Güte der Trennbarkeit zweier Klassen in einem… … Deutsch Wikipedia
 - Vektorraum.
- Vektorraum. 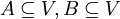 heißen linear separierbar, wenn n+1 reelle Zahlen
heißen linear separierbar, wenn n+1 reelle Zahlen 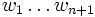 existieren, mit:
existieren, mit: 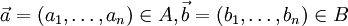 gilt
gilt 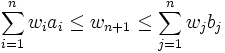
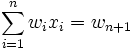 bilden die separierende Hyperebene.
bilden die separierende Hyperebene.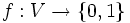 ) heißen linear separierbar, wenn die Urbilder von 0 und 1 separierbar sind. Die linear separierbare Funktionen spielen beim maschinellen Lernen eine Rolle. So kann zum Beispiel das einfache Perzeptron nur linear trennbare Funktionen lernen.
) heißen linear separierbar, wenn die Urbilder von 0 und 1 separierbar sind. Die linear separierbare Funktionen spielen beim maschinellen Lernen eine Rolle. So kann zum Beispiel das einfache Perzeptron nur linear trennbare Funktionen lernen.