- Urbild (Mathematik)
-
In der Mathematik ist das Urbild ein Begriff im Zusammenhang mit Funktionen. Das Urbild einer Menge M unter einer Funktion f ist die Menge der Elemente, die in f eingesetzt, ein Element aus M ergeben. Ist also y aus M und f(x) = y, dann ist x Element des Urbildes von M unter f. Speziell besteht das Urbild eines Elements y der Zielmenge aus allen Elementen des Definitionsbereichs, die durch f auf y abgebildet werden. Damit ist das Urbild eine Teilmenge des Definitionsbereichs.
Inhaltsverzeichnis
Definition
Sei
 eine Funktion und M eine Teilmenge von B. Dann bezeichnet man folgende Menge als das Urbild von M unter f:
eine Funktion und M eine Teilmenge von B. Dann bezeichnet man folgende Menge als das Urbild von M unter f:Ein Urbild ist damit ein Wert der sogenannten Urbildfunktion, die von der Potenzmenge 2B der Zielmenge B in die Potenzmenge 2A des Definitionsbereiches A abbildet.
Das Urbild einer einelementigen Menge M = {b} schreibt man auch als
und nennt es das Urbild von b unter f. Diese Menge braucht aber nicht einelementig zu sein (sie kann also auch leer sein oder mehr als ein Element enthalten).
Das Urbild eines Elements wird zuweilen auch Faser dieses Elements genannt, insbesondere im Zusammenhang mit Faserbündeln.
Beispiele
Für die Funktion
 (ganze Zahlen) mit
(ganze Zahlen) mit  gilt:
gilt:Eigenschaften
Injektivität, Surjektivität, Bijektivität
- Unter einer bijektiven Funktion
 ist das Urbild jedes Elements (genau) einelementig. Die Abbildung, die jedem Element von B das (einzige, also eindeutig bestimmte) Element seines Urbildes zuordnet, heißt Umkehrfunktion von f. Man bezeichnet sie (auch – wie die Urbildfunktion) mit f − 1. Das kann leicht zu Missverständnissen führen, wenn man nicht ausführlicher
ist das Urbild jedes Elements (genau) einelementig. Die Abbildung, die jedem Element von B das (einzige, also eindeutig bestimmte) Element seines Urbildes zuordnet, heißt Umkehrfunktion von f. Man bezeichnet sie (auch – wie die Urbildfunktion) mit f − 1. Das kann leicht zu Missverständnissen führen, wenn man nicht ausführlicher  für die Umkehrfunktion schreibt (wodurch sie dann deutlich von der Urbildfunktion
für die Umkehrfunktion schreibt (wodurch sie dann deutlich von der Urbildfunktion  unterschieden wird).
unterschieden wird). - Unter einer injektiven Funktion ist das Urbild eines Elements höchstens einelementig (also stets einelementig oder leer).
- Unter einer surjektiven Funktion ist das Urbild eines Elements mindestens einelementig (also stets nichtleer).
Mengenoperationen und -eigenschaften
Es sei
 eine Funktion, und M und N seien Teilmengen von B :
eine Funktion, und M und N seien Teilmengen von B :Dabei bezeichnet
 das Komplement von X in der jeweiligen Grundmenge.
das Komplement von X in der jeweiligen Grundmenge.Die Aussagen über Vereinigung und Durchschnitt lassen sich von zwei Teilmengen auf beliebige Familien von Teilmengen verallgemeinern.
Bild und Urbild
Es sei
 eine Funktion, M eine Teilmenge von A und N eine Teilmenge von B :
eine Funktion, M eine Teilmenge von A und N eine Teilmenge von B :
Ist f injektiv, dann gilt die Gleichheit.
Ist N im Bild von f enthalten, dann gilt die Gleichheit. Insbesondere gilt sie also, wenn f surjektiv ist.
Siehe auch
Kategorie:- Mathematischer Grundbegriff
Wikimedia Foundation.

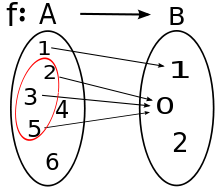
 ist die Menge
ist die Menge 












