- Lorenzkurve
-
Dieser Artikel beschreibt die Lorenzkurve zur Darstellung von Verteilungen. Für die Lorentz-Kurve siehe Cauchy-Verteilung.
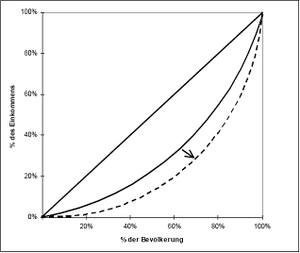
Die Lorenz-Kurve (auch Lorenzkurve) wurde 1905 von Max Otto Lorenz zur grafischen Darstellung von statistischen Verteilungen und der Veranschaulichung des Ausmaßes an Konzentration bzw. Ungleichheit eingeführt. Sie wird insbesondere zur Analyse der Einkommensverteilung verwendet.
Inhaltsverzeichnis |
Eigenschaften der Lorenz-Kurve
Die Lorenzkurve hat drei charakteristische Eigenschaften:
Der Graph ist in jedem Fall monoton steigend und befindet sich immer unter (ggf. auch auf) der 45° Linie der Nullkonzentration (in der Grafik als "Gleichverteilung" bezeichnet). Die Lorenzkurve kann nur gleich der Linie der Nullkonzentration sein, wenn es sich um eine Ein-Punkt-Verteilung handelt.
Die Fläche zwischen Nullkonzentration und Lorenzkurve wird maximal für einen Monopolisten-Markt. Dieser Zustand wird im Gegensatz zur Nullkonzentration als "maximale Konzentration" bezeichnet.
Zustandekommen der Lorenzkurve
Bei der Lorenzkurve wird eine bestimmte Größe aufsteigend (d. h. beim kleinsten Wert beginnend) sortiert und anschließend kumuliert („aufaddiert“). Dadurch entsteht der charakteristische Bauch der Lorenzkurve, welcher anschaulich das Maß der Ungleichverteilung angibt.
Beispieltabelle einer Lorenzkurve
| i | Fi | qi | Qi |
|---|---|---|---|
| 1 | 0,1 | 0,025 | 0,025 |
| 2 | 0,2 | 0,025 | 0,050 |
| 3 | 0,3 | 0,025 | 0,075 |
| 4 | 0,4 | 0,025 | 0,100 |
| 5 | 0,5 | 0,050 | 0,150 |
| 6 | 0,6 | 0,050 | 0,200 |
| 7 | 0,7 | 0,100 | 0,300 |
| 8 | 0,8 | 0,100 | 0,400 |
| 9 | 0,9 | 0,100 | 0,500 |
| 10 | 1,0 | 0,500 | 1,000 |
Erläuterung:
Hier handelt es sich um zehn Objekte ("Merkmalsträger", z. B. Firmen), bei denen jeweils ein bestimmter Wert des Merkmals (z. B. Umsatz) vorliegt. Diese Merkmalsträger sind in der Tabelle nach der Größe des Merkmals geordnet.
Die Spalte Fi enthält den kumulierten Anteil der Merkmalsträger (den Anteil der Merkmalsträger, die bis zur jeweiligen Zeile aufgeführt sind), die Spalte qi enthält den Anteil, den der Merkmalsträger zum Gesamtwert beiträgt (zwischen 2,5 % und 50 %). In der Spalte Qi sind diese Anteile kumuliert.
Die Lorenzkurze entsteht, indem man Qi über Fi aufträgt.
Satz von Rothschild & Stiglitz
Gegeben seien zwei Verteilungen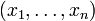 
und 
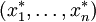mit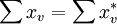 
. Die Lorenzkurve von 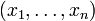liegt oberhalb der Lorenzkurve von 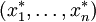. Dann und nur dann gilt: 
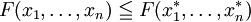für jede symmetrische und quasikonvexe Funktion F.
Folgerung: Wenn sich zwei Lorenzkurven schneiden, hängt es von der Wahl der jeweiligen symmetrischen und quasikonvexen Funktion F ab, welche der beiden Kurven als die mit der größeren Ungleichheit zu bezeichnen ist.
Anwendungsgebiete
Neben der Illustration der Einkommensverteilung wird die Lorenz-Kurve auch zur Darstellung von Marktmacht (Konzentrationsverteilung, beispielsweise gemessen an Unternehmensumsätzen) oder räumlichen Verteilungen verwendet (vergleiche Segregation).
Eine weitere Anwendung findet die Lorenzkurve in der logistischen ABC-Analyse, bei der die Lorenzkurve die Verteilung der Güter verdeutlicht, geordnet nach Klassifizierungseigenschaft (beispielsweise Wert) und Verbrauchsmenge.
Beispiel Marktwirtschaft: Bei kleiner Anbieterzahl liefert Lorenz ggf. – je nach Anwendungsgebiet – keine realitätsnahen Ergebnisse. Bei zwei Anbietern, die sich einen Markt zu je 50 % teilen, liefert Lorenz hier eine Nullkonzentration, obgleich es sich um ein Oligopol handelt – also keinesfalls eine ideale Marktwirtschaft mit unendlich vielen kleinen Anbietern. Eine Alternative bieten andere Ungleichverteilungsmaße oder die absolute Konzentrationsanalyse nach Herfindahl (Herfindahl-Index).
Siehe auch
Weblinks
Wikimedia Foundation.
