- Konvexe und konkave Funktionen
-
In der Analysis heißt eine Funktion f von einem Intervall I (oder allgemeiner einer konvexen Teilmenge C eines reellen Vektorraums) nach
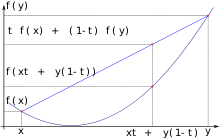
 konvex, wenn für alle x,y aus I (bzw. aus C) und t zwischen 0 und 1 gilt
konvex, wenn für alle x,y aus I (bzw. aus C) und t zwischen 0 und 1 giltAnschaulich bedeutet die Definition: Die Funktionswerte zwischen zwei Werten x,y liegen unterhalb oder auf der Verbindungsgeraden der beiden Funktionswerte an x und y.
Gilt das Ungleichheitszeichen in die umgekehrte Richtung, also
für alle x, y aus I und t zwischen 0 und 1, so wird die Funktion als konkav bezeichnet.[1]
Um Missverständlichkeiten im Zusammenhang mit der anschaulich-geometrischen Bedeutung beider Begriffe vorzubeugen, präzisiert man die Begriffe „konvex“ und „konkav“ im hier diskutierten Kontext zuweilen noch einmal durch zusätzliche Angabe einer Blickrichtung, also beispielsweise den hier verwendeten Begriff „konvex“ als „konvex von unten“ und den Begriff „konkav“ – im Gegensatz dazu – als „konvex von oben“.[2]
Eine Funktion heißt streng konvex oder strikt konvex, wenn für alle
 aus I (bzw. C) und t echt zwischen 0 und 1 gilt
aus I (bzw. C) und t echt zwischen 0 und 1 giltAnalog heißt eine Funktion streng konkav oder strikt konkav, wenn für alle
 aus I (bzw. C) und t echt zwischen 0 und 1 gilt
aus I (bzw. C) und t echt zwischen 0 und 1 giltDie besondere Bedeutung konvexer bzw. konkaver Funktionen liegt darin, dass sie allgemeiner als lineare Funktionen sind, aber einfach zu untersuchende Eigenschaften haben, die viele Aussagen über nichtlineare Systeme, beispielsweise in der konvexen Optimierung, ermöglichen.
Inhaltsverzeichnis
- 1 Geschichte
- 2 Eigenschaften
- 3 Beispiele
- 4 Konvexität, Beschränktheit und Stetigkeit
- 5 Quellen
- 6 Siehe auch
- 7 Weblinks
Geschichte
Wesentliche Aussagen zu konvexen und konkaven Funktionen finden sich bereits 1889 bei Otto Hölder, wobei er aber die Bezeichnungen konvex und konkav noch nicht verwendete.[3] Die Bezeichnungen konvex und konkav für Funktionen wurden 1905 von Johann Ludwig Jensen eingeführt.[4] Jensen verwendete dazu allerdings noch die gelegentlich, vor allem in älteren Werken [5] anzutreffende schwächere Definition
für die er zeigte, dass daraus für stetige Funktionen die eingangs genannte Ungleichung
für alle t zwischen 0 und 1 folgt.[6] Für Details siehe jensensche Ungleichung.
Eigenschaften
Graph
Der Graph einer konvexen Funktion ist so gewölbt, dass die Menge der Punkte oberhalb des Graphen, der sogenannte Epigraph, eine konvexe Menge ist. Zu beachten ist, dass eine nicht-konvexe Funktion nicht automatisch konkav sein muss, d. h., konvex und konkav sind hier nicht komplementär. Jede lineare Funktion ist sowohl konkav als auch konvex. Die kubische Funktion
 ist im Bereich aller positiven x-Werte streng konvex und im Bereich aller negativen x-Werte streng konkav. Somit ist diese Funktion über ganz
ist im Bereich aller positiven x-Werte streng konvex und im Bereich aller negativen x-Werte streng konkav. Somit ist diese Funktion über ganz  weder konvex noch konkav.
weder konvex noch konkav.Verhältnis konvex und konkav
Eine Funktion f ist genau dann konvex (konkav), wenn die Funktion − f konkav (konvex) ist.
Umkehrfunktion
Ist f invertierbar und setzt man x = f − 1(u),y = f − 1(v), so erhält man für eine konvexe Funktion
Für eine monoton steigende Funktion gilt also
Für eine invertierbare, monoton steigende und konvexe (konkave) Funktion hat daher die Umkehrfunktion die umgekehrte Art der Konvexität, ist also monoton steigend und konkav (konvex), siehe z. B. ex und ln x.
Für eine monoton fallende Funktion gilt hingegen
Für eine invertierbare monoton fallende und konvexe (konkave) Funktion hat daher die Umkehrfunktion die gleiche Art der Konvexität, ist also streng monoton fallend und konvex (konkav), siehe z. B. 1 / x auf
 bzw.
bzw.  .
.Konvexität und erste Ableitung
Ist
 differenzierbar, dann gilt
differenzierbar, dann gilt- f ist genau dann konvex, wenn ihre Ableitung
 wachsend ist, und genau dann streng konvex, wenn
wachsend ist, und genau dann streng konvex, wenn  streng monoton wachsend ist. f ist genau dann konkav, wenn ihre Ableitung
streng monoton wachsend ist. f ist genau dann konkav, wenn ihre Ableitung  fallend ist, und genau dann streng konkav, wenn
fallend ist, und genau dann streng konkav, wenn  streng monoton fallend ist. Dieses Resultat findet sich im Wesentlichen schon 1889 bei Otto Hölder.[3]
streng monoton fallend ist. Dieses Resultat findet sich im Wesentlichen schon 1889 bei Otto Hölder.[3] - Konvexe Funktionen liegen oberhalb der Tangente, also
 , wobei für streng konvexe Funktionen außerdem
, wobei für streng konvexe Funktionen außerdem  für
für  gilt, woraus beispielsweise die Verallgemeinerung der bernoullischen Ungleichung
gilt, woraus beispielsweise die Verallgemeinerung der bernoullischen Ungleichung  für reelle r mit
für reelle r mit  oder
oder  folgt.
folgt. - Konkave Funktionen liegen unterhalb der Tangente, also
 , wobei für streng konkave Funktionen außerdem
, wobei für streng konkave Funktionen außerdem  für
für  gilt, woraus beispielsweise die Verallgemeinerung der bernoullischen Ungleichung
gilt, woraus beispielsweise die Verallgemeinerung der bernoullischen Ungleichung  für reelle r mit
für reelle r mit  folgt.
folgt. - Eine konvexe (konkave) Funktion ist fast überall differenzierbar
Alternativ:
- Jede konvexe (konkave) Funktion ist im Inneren links- und rechtsseitig differenzierbar.
- Eine überall links- und rechtsdifferenzierbare Funktion ist genau dann konvex, wenn ihre Ableitung monoton wachsend ist.
- Eine überall links- und rechtsdifferenzierbare Funktion ist genau dann konkav, wenn ihre Ableitung monoton fallend ist.
Konvexität und zweite Ableitung
Der Zusammenhang zwischen Konvexität und zweiter Ableitung wurde im Wesentlichen schon 1889 von Otto Hölder beschrieben.[3] Für zweimal differenzierbare Funktionen
 gilt:
gilt: ist genau dann konvex, wenn
ist genau dann konvex, wenn  gilt. Ist
gilt. Ist  durchweg positiv,
durchweg positiv,  also stets linksgekrümmt, ist
also stets linksgekrümmt, ist  damit zugleich streng konvex; bei einfacher Konvexität dagegen kann die zweite Ableitung auch einzelne Nullstellen, d.h. die Funktion selbst einzelne nicht gekrümmte Stellen besitzen, wie etwa f(x) = x4 an der Stelle x = 0.
damit zugleich streng konvex; bei einfacher Konvexität dagegen kann die zweite Ableitung auch einzelne Nullstellen, d.h. die Funktion selbst einzelne nicht gekrümmte Stellen besitzen, wie etwa f(x) = x4 an der Stelle x = 0. ist genau dann konkav, wenn
ist genau dann konkav, wenn  gilt. Ist
gilt. Ist  durchweg negativ,
durchweg negativ,  also stets rechtsgekrümmt, ist
also stets rechtsgekrümmt, ist  damit zugleich streng konkav; bei einfacher Konkavität dagegen kann die zweite Ableitung auch einzelne Nullstellen, d.h. die Funktion selbst einzelne nicht gekrümmte Stellen besitzen, wie etwa f(x) = − x4 an der Stelle x = 0.
damit zugleich streng konkav; bei einfacher Konkavität dagegen kann die zweite Ableitung auch einzelne Nullstellen, d.h. die Funktion selbst einzelne nicht gekrümmte Stellen besitzen, wie etwa f(x) = − x4 an der Stelle x = 0.
Ist die Funktion
 zweimal stetig differenzierbar, dann gilt
zweimal stetig differenzierbar, dann gilt- f ist genau dann konvex, wenn die Hesse-Matrix von f positiv semidefinit ist. Ist die Hesse-Matrix von f positiv definit, so ist f strikt konvex.
- f ist genau dann konkav, wenn die Hesse-Matrix von f negativ semidefinit ist. Ist die Hesse-Matrix von f negativ definit, so ist f strikt konkav.
Extremwerte
- Ein lokales Minimum einer konvexen Funktion ist auch ein globales Minimum. Eine strikt konvexe Funktion hat höchstens ein globales Minimum. Eine stetige strikt konvexe Funktion auf einer kompakten konvexen Menge hat auf dieser Menge genau ein globales Minimum. ex hat aber beispielsweise kein globales Minimum für
 .
. - Ein lokales Maximum einer konkaven Funktion ist auch ein globales Maximum. Eine strikt konkave Funktion hat höchstens ein globales Maximum. Eine stetige strikt konkave Funktion auf einer kompakten konvexen Menge hat auf dieser Menge genau ein globales Maximum. ln x hat aber beispielsweise kein globales Maximum für
 .
.
Da konvexe bzw. konkave Funktionen die Eindeutigkeit von Extremwerten sicherstellen, spielen sie in der nicht-linearen Optimierung eine wichtige Rolle.
Verknüpfungen
Linearkombination
Sind f und g zwei konvexe (konkave) Funktionen, so ist auch jede Linearkombination af + bg mit nichtnegativen Koeffizienten a,b wieder konvex (konkav).
Grenzwert
Der Grenzwert einer punktweise konvergenten Folge konvexer (konkaver) Funktionen ist auch wieder eine konvexe (konkave) Funktion. Ebenso ist die Summe einer punktweise konvergenten Reihe konvexer (konkaver) Funktionen auch wieder eine konvexe (konkave) Funktion.
Supremum konvexer Funktionen
Ist
 eine Menge konvexer Funktionen und existiert punktweise das Supremum
eine Menge konvexer Funktionen und existiert punktweise das Supremumfür alle x, so ist auch f eine konvexe Funktion.
Für das Infimum gilt das nicht, wie das Beispiel f1(x) = 1, f2(x) = x zeigt.
Infimum konkaver Funktionen
Ist
 eine Menge konkaver Funktionen, und existiert punktweise das Infimum
eine Menge konkaver Funktionen, und existiert punktweise das Infimumfür alle x, so ist auch f eine konkave Funktion.
Für das Supremum gilt das nicht, wie das Beispiel f1(x) = 1, f2(x) = x zeigt.
Jensensche Ungleichung
Für konvexe und konkave Funktionen gilt die jensensche Ungleichung.
Der Fall t<0 bzw. t>1
Für t < 0 oder t > 1 dreht sich das Ungleichheitszeichen um, für konvexe Funktionen gilt dann also
sofern u: = tx + (1 − t)y noch im Intervall I (bzw. in der konvexen Menge C) ist. Um das zu sehen, sei beispielsweise t > 1, dann gilt
 , wegen Konvexität also
, wegen Konvexität alsosomit
Konvexität und Stetigkeit
Jede auf einem offenen Intervall definierte konvexe Funktion ist stetig. Setzt man umgekehrt Stetigkeit voraus, so reicht für Konvexität bereits die Bedingung, dass für alle x,y aus I gilt
es reicht sogar, dass für ein beliebiges, aber fixes λ mit 0 < λ < 1
für alle x,y aus I gilt.
Beispiele
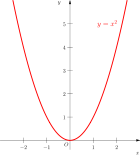
- Die Funktion f(x) = x2 ist auf ganz
 streng konvex, denn
streng konvex, denn  ist streng monoton wachsend.
ist streng monoton wachsend. - Die Funktion f(x) = − x2 ist auf ganz
 streng konkav, denn
streng konkav, denn  ist streng monoton fallend.
ist streng monoton fallend. - Die Wurzelfunktion
 ist streng konkav auf dem Intervall
ist streng konkav auf dem Intervall  der nichtnegativen reellen Zahlen.
der nichtnegativen reellen Zahlen. - Die Exponentialfunktion ist streng konvex auf ganz
 .
. - Die Logarithmusfunktion ist streng konkav auf dem Intervall
 für eine Basis größer als 1 und streng konvex auf dem Intervall
für eine Basis größer als 1 und streng konvex auf dem Intervall  für eine Basis kleiner als 1.
für eine Basis kleiner als 1. - Die Betragsfunktion f(x) = | x | ist auf ganz
 konvex, aber nicht streng konvex.
konvex, aber nicht streng konvex. - Die negative Betragsfunktion f(x) = − | x | ist auf ganz
 konkav, aber nicht streng konkav.
konkav, aber nicht streng konkav. - Die Funktion f(x) = x3 ist konkav für
 und konvex für
und konvex für  .
. - Die Funktion
 ist streng konvex auf dem Intervall
ist streng konvex auf dem Intervall  der positiven reellen Zahlen und streng konkav auf dem Intervall
der positiven reellen Zahlen und streng konkav auf dem Intervall  der negativen reellen Zahlen.
der negativen reellen Zahlen.
Konvexität, Beschränktheit und Stetigkeit
Schwächere Definition der Konvexität
Setzt man Stetigkeit voraus, so reicht für Konvexität in einer konvexen Teilmenge C eines reellen topologischen Vektorraums bereits die Bedingung, dass ein beliebiges, aber fixes
 mit 0 < λ < 1 existiert, sodass für alle x,y aus C gilt:
mit 0 < λ < 1 existiert, sodass für alle x,y aus C gilt:Um dies zu sehen, betrachtet man die Menge T aller „guten“ t, die durch
definiert ist.
Seien nun
 . Dann gilt auch
. Dann gilt auch  , denn
, dennSein nun t eine beliebige reelle Zahl mit 0 < t < 1. Dann lässt sich eine Intervallschachtelung [un,vn] mit
 konstruieren, die gegen t konvergiert: Sei u0 = 0,v0 = 1 und
konstruieren, die gegen t konvergiert: Sei u0 = 0,v0 = 1 und  und
und  mit
mit  .
.Sei
 .
.Ist
 , so setzt man
, so setzt man  ,
,  , und es gilt
, und es gilt  .
.Ist
 , so setzt man
, so setzt man  ,
,  , und es gilt
, und es gilt  .
. sind ebenfalls aus
sind ebenfalls aus  , es gilt
, es gilt ![t\in[u_{n+1}, v_{n+1}]\!](4/074e277f37bc81364a30799d298a81c2.png) und
und  .
.Die so konstruierte Intervallschachtelung konvergiert also gegen
 ; wegen der Stetigkeit von
; wegen der Stetigkeit von  gilt daher
gilt daher  . Da
. Da  beliebig gewählt war, folgt also
beliebig gewählt war, folgt also ![T=[0,1]\!](4/174cf9fa49713bf168f8abf5d85c6ca6.png) , und
, und  ist konvex.
ist konvex.Gegenbeispiel ohne Stetigkeit
Dass Stetigkeit für die schwächere Definition wirklich benötigt wird, lässt sich mit folgendem Gegenbeispiel zeigen: Ist bj
 eine Hamelbasis des Vektorraums der reellen Zahlen über dem Körper der rationalen Zahlen, also eine über den rationalen Zahlen linear unabhängige Menge reeller Zahlen, in der jede reelle Zahl r eine Darstellung der Art
eine Hamelbasis des Vektorraums der reellen Zahlen über dem Körper der rationalen Zahlen, also eine über den rationalen Zahlen linear unabhängige Menge reeller Zahlen, in der jede reelle Zahl r eine Darstellung der Art  mit nur endlich vielen rationalen
mit nur endlich vielen rationalen  hat, so erfüllt bei beliebiger Wahl von f(bj) die Funktion
hat, so erfüllt bei beliebiger Wahl von f(bj) die Funktion  zwar
zwar  ist aber nicht notwendigerweise konvex.
ist aber nicht notwendigerweise konvex.Beschränktheit und Konvexität
Setzt man für eine Funktion f zusätzlich zur Bedingung, dass für ein fixes
 die Beziehung
die Beziehungfür alle x,y aus einer konvexen Teilmenge C eines normierten Vektorraums gilt, noch voraus, dass f nach oben beschränkt ist, so folgt daraus bereits die Stetigkeit von f in den inneren Punkten von C. Anschaulich wird dies daraus klar, dass man an einer Unstetigkeitsstelle eine beliebig steile Verbindungsgerade zwischen zwei Funktionswerten ziehen kann, wobei die Funktion zwischen den beiden Werten unterhalb der Verbindungsgeraden und außerhalb der beiden Werte oberhalb der Verbindungsgerade liegen muss. Kann die Verbindungsgerade nun beliebig steil werden, so stößt man irgendwann über die obere Schranke der Funktion.
Formal ist der Beweis allerdings etwas komplizierter. Zunächst beachte man, dass aus den obigen Voraussetzungen für natürliche Zahlen n und
folgt, dass
bzw.
Sei nun a ein beliebiger innerer Punkt von C und
eine zur Gänze in C enthaltene offene Kugel um a. Wäre nun f nicht stetig in a, so gäbe es ein ε > 0, so dass für jedes δ > 0 ein x existiert, so dass zwar
 , aber | f(x) − f(a) | > ε. Sein nun
, aber | f(x) − f(a) | > ε. Sein nun  so gewählt, dass
so gewählt, dasswobei M eine obere Schranke für f sei. Wählt man nun
 , so existiert also ein x mit
, so existiert also ein x mit ,
,
aber
- | f(x) − f(a) | > ε.
Angenommen,
 . Dann gilt für
. Dann gilt für 
Das kann aber nicht sein, da
 . Daher liegt y in C, und es muss f(y) < M gelten.
. Daher liegt y in C, und es muss f(y) < M gelten.Sei daher
 . Dann gilt für
. Dann gilt für 
Das kann aber auch nicht sein, da
 . Daher liegt auch z in C, und es muss ebenfalls f(z) < M gelten.
. Daher liegt auch z in C, und es muss ebenfalls f(z) < M gelten.f muss daher stetig in a sein.
Die Aussage, dass eine konvexe beschränkte Funktion stetig in den inneren Punkten ist, ist auch bedeutsam für das Lösen der cauchyschen Funktionalgleichung
- f(x + y) = f(x) + f(y)
- f(1) = a.
Aus dieser Aussage folgt nämlich, dass diese Funktionalgleichung eine eindeutige Lösung hat, wenn zusätzlich gefordert wird, dass f beschränkt ist.
Unendlichdimensionaler Fall
Im unendlichdimensionalen Fall brauchen konvexe Funktionen nicht stetig zu sein, da es lineare (also somit auch konvexe) Funktionale gibt, die nicht stetig sind. Allerdings gilt, dass beschränkte konvexe Funktionale eines normierten Vektorraums stetig sind.
Endlichdimensionaler Fall
Innere Punkte
Konvexe Funktionen f einer konvexen Teilmenge C des endlichdimensionalen reellen Vektorraums
 sind stetig in den inneren Punkten. Um das zu sehen, betrachte man einen inneren Punkt
sind stetig in den inneren Punkten. Um das zu sehen, betrachte man einen inneren Punkt  . Für diesen existiert ein Simplex
. Für diesen existiert ein Simplex  mit den Eckpunkten
mit den Eckpunkten  , der a wieder als inneren Punkt enthält. Jeder Punkt
, der a wieder als inneren Punkt enthält. Jeder Punkt  ist aber in der Form
ist aber in der Formmit
und
 für alle j darstellbar. Nach der jensenschen Ungleichung gilt nun
für alle j darstellbar. Nach der jensenschen Ungleichung gilt nun .
.
f ist daher nach oben beschränkt und somit, wie oben gezeigt wurde, stetig im inneren Punkt a.
Randpunkte
In Randpunkten können konvexe Funktionen unstetig sein, wie das Beispiel der Funktion
 mit
mitzeigt, die zwar konvex ist, aber am Randpunkt x = 0 eine Unstetigkeit aufweist.
Quellen
- ↑ a b Harro Heuser, Lehrbuch der Analysis (Teil 1), 10. Auflage, B. G. Teubner, Stuttgart, 1993, ISBN 3-519-32231-5. (49.2)
- ↑ z. B. in I. N. Bronstein, K. A. Semendjajew, Taschenbuch der Mathematik, 19. Auflage, BSB B.G. Teubner, Leipzig, 1979. 3.1.5.4 Monotonie und Konvexität von Funktionen
- ↑ a b c O. Hölder Ueber einen Mittelwerthssatz. Nachrichten von der Königl. Gesellschaft der Wissenschaften und der Georg-Augusts-Universität zu Göttingen 1889, S. 38ff.
- ↑ Earliest Known Uses of Some of the Words of Mathematics, 28. Juli 2006: A. Guerraggio and E. Molho write, „The first modern formalization of the concept of convex function appears in J. L. W. V. Jensen Om konvexe funktioner og uligheder mellem midelvaerdier, Nyt Tidsskr. Math. B 16 (1905), S. 49–69. Since then, at first referring to Jensen’s convex functions, then more openly, without needing any explicit reference, the definition of convex function becomes a standard element in calculus handbooks.“ („The Origins of Quasi-concavity: a Development between Mathematics and Economics,“ Historia Mathematica, 31, (2004), 62–75.)
- ↑ z. B. in I. P. Natanson, Theorie der Funktionen einer reellen Veränderlichen, 4. Auflage, Verlag Harri Deutsch, Thun, 1981, ISBN 3-87144-217-8.
- ↑ Jensen, J. L. W. V. Sur les fonctions convexes et les inégalités entre les valeurs moyennes. In Acta Math. 30, 175–193, 1906.
Siehe auch
Weblinks
Wikimedia Foundation.


















![T=\lbrace t \in [0,1]: f(t x+(1-t)y) \le t f(x)+(1-t)f(y) \quad \forall x,y \in C\rbrace](b/6fb67587a4f15f8b9b35b77e74ecded9.png)











