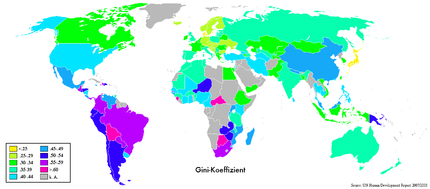
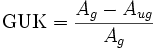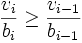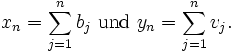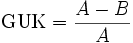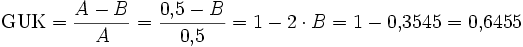Giniindex

Dieser Artikel oder Abschnitt bedarf einer Überarbeitung. Näheres ist auf der Diskussionsseite angegeben. Hilf mit, ihn zu verbessern, und entferne anschließend diese Markierung.

Anwendung des Gini-Koeffizienten zur Bestimmung von Einkommensungleichheit

Der Gini-Koeffizient oder auch Gini-Index ist ein statistisches Maß, das vom italienischen Statistiker Corrado Gini zur Darstellung von Ungleichverteilungen entwickelt wurde. Der Koeffizient kann beispielsweise als Kennzahl für die Ungleichverteilung von Einkommen oder Vermögen eingesetzt werden. Er wird besonders in der Wohlfahrtsökonomie verwendet.

Der Wert kann beliebige Größen zwischen 0 und 1 (bzw. 0 und 100 Prozent) annehmen. Je näher der Gini-Koeffizient an 1 ist, desto größer ist die Ungleichheit (zum Beispiel einer Einkommensverteilung).

Berechnung

Der Gini-Koeffizient ist die auf die gleichverteilte Gesellschaft normierte Fläche zwischen den Lorenz-Kurven einer gleichverteilten und der beobachteten Gesellschaft.

$\mbox {GUK} = \frac {A_g-A_{ug}} {A_g}$

mit A_g der Fläche unter der Lorenz-Kurve einer gleichverteilten Gesellschaft und A_ug der Fläche unter der Lorenz-Kurve für die beobachtete Gesellschaft.

Beispiel zur Berechnung

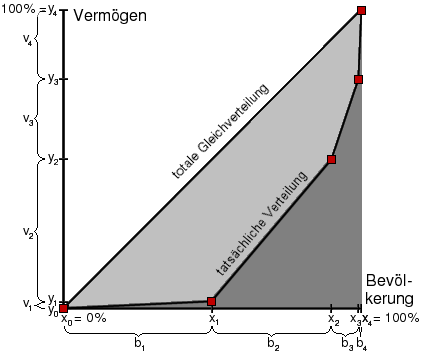
Ungleichverteilungskoeffizienten lassen sich nicht nur für Einkommensverteilungen, sondern auch für Vermögensverteilungen berechnen. Wie man die Ungleichverteilung berechnet, zeigt der folgende Beitrag anhand der Verteilung eines „Gesamtvermögens“ von etwa 10 Billionen Deutschen Mark in Deutschland (1995)^[1]:

50 Prozent der Bevölkerung (b1) besaßen  2,5 Prozent des Vermögens (v1).
40 Prozent der Bevölkerung (b2) besaßen 47,5 Prozent des Vermögens (v2).
 9 Prozent der Bevölkerung (b3) besaßen 27,0 Prozent des Vermögens (v3).
 1 Prozent der Bevölkerung (b4) besaß   23,0 Prozent des Vermögens (v4).

In einem ersten Schritt werden die Daten „normalisiert“ dargestellt:

b1 = 0,50     v1 = 0,025          v1/b1 =  0,05
b2 = 0,40     v2 = 0,475          v2/b2 =  1,188
b3 = 0,09     v3 = 0,270          v3/b3 =  3
b4 = 0,01     v4 = 0,230          v4/b4 = 23

Im zweiten Schritt wird der Gini-Koeffizient berechnet.

Den Gini-Ungleichverteilungskoeffizient (GUK) erhält man durch Auswertung einer Lorenz-Kurve.

Damit tatsächlich eine Lorenz-Kurve entsteht, müssen gegebenenfalls die obigen Werte umsortiert werden. Alle Werte-Paare (v_i,b_i) müssen zunächst so vorsortiert werden, dass gilt:

$\frac {v_i} {b_i} \ge \frac {v_{i-1}} {b_{i-1}}$

Bei dem obigen Beispiel liegt schon die richtige Sortierung vor, so dass nicht umsortiert werden muss.

Die gesuchte Lorenz-Kurve entsteht, wenn man (x_i,y_i)-Paare als Punkte in ein kartesisches Koordinatensystem einträgt und anschließend benachbarte Punkte mit einer Geraden verbindet. Die (x_i,y_i)-Paare entstehen aus den (v_i,b_i)-Paaren nach folgender Rechenvorschrift:

$x_n = \sum_{j=1}^n b_j \mbox { und } y_n = \sum_{j=1}^n v_j.$

Im zweiten Schritt werden aus den Daten des ersten Schritts die nachfolgenden Daten durch Summation ermittelt (wobei am Anfang 1 fester Wert dazu kommt):

x0 = 0,00     y0 = 0
x1 = 0,50     y1 = 0,025
x2 = 0,90     y2 = 0,5    (da 0,5 + 0,4 = 0,9 und 0,025 + 0,475 = 0,5 ist)
x3 = 0,99     y3 = 0,77
x4 = 1,00     y4 = 1

Bei totaler Gleichverteilung ist die Lorenz-Kurve eine gerade Linie von Punkt 0/0 zu Punkt 1/1.

Zur Bestimmung des Gini-Koeffizienten werden zuerst zwei Größen bestimmt, die graphisch betrachtet Flächen sind. Einmal die Fläche unter der Gleichverteilungslinie, nennen wir diese Größe beispielsweise A. Die zweite Fläche ist die Fläche unter der tatsächlichen Verteilungskurve, nennen wir diese Größe beispielsweise B. Mit diesen beiden Größen berechnet sich der Gini-Ungleichverteilungskoeffizient wie folgt:

$\mbox {GUK} = \frac {A-B} {A}$

B ist die dunkelgraue Fläche; A setzt sich aus der hell- und der dunkelgrauen Fläche zusammen.

Errechnen der y-Werte der Lorenz-Kurve der tatsächlichen Verteilung:

y0 = 0,000
y1 = v1 = 0,025
y2 = v1 + v2 = 0,500
y3 = v1 + v2 + v3 = 0,770
y4 = v1 + v2 + v3 + v4 = 1,000

Berechnung der Fläche B unter der Lorenz-Kurve der tatsächlichen Verteilung (siehe unten):

(y1 - 0,5 · v1) · b1 = 0,00625
(y2 - 0,5 · v2) · b2 = 0,105
(y3 - 0,5 · v3) · b3 = 0,05715
(y4 - 0,5 · v4) · b4 = 0,00885

B = 0,17725

Da eine normierte Darstellung verwendet wird, verbindet die Kurve der totalen Gleichverteilung die Eckpunkte (0|0) und (1|1). Das Dreieck Fläche A beträgt also 0,5. Darum gilt für den Gini-Ungleichverteilungskoeffizienten:

$\mbox {GUK} = \frac {A - B}{A} = \frac {0{,}5 - B}{0{,}5} = 1 - 2 \cdot B = 1 - 0{,}3545 = 0{,}6455$ ^[2]

Graphisch betrachtet ist der Gini-Koeffizient das Verhältnis der Fläche zwischen Gleichverteilungslinie und Lorenzkurve (A-B) zur Fläche unterhalb der Gleichverteilungslinie (A).

Erläuterung zur Berechnung

Die gesamte Gini-Fläche ist ein Rechteck mit den Seiten v₁ + v₂ + v₃ + v₄ mal b₁ + b₂ + b₃ + b₄. Die ideale Gini-Fläche ist die Hälfte der gesamten Gini-Fläche. Zur Berechnung der Fläche unter der Kurve werden alle Einzelflächen addiert. Nehmen wir beispielsweise b₂. Voll anzurechnen ist das Rechteck mit der Höhe y₁ und der Breite b₂ (d. h. von x₁ bis x₂). Von dem Rechteck, das von der Höhe y₁ bis zur Höhe y₂ geht ist nur die Hälfte zu nehmen, da die andere Hälfte oberhalb der Ginilinie nicht zur Gini-Fläche gehört. Also ist die

Fläche $= y_1 \cdot b_2 + \frac{(y_2 - y_1)\cdot b_2}{2} = \frac{(y_2 + y_1) \cdot b_2}{2}$

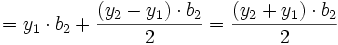
oder auch

Fläche $= (y_2 - \frac{v_2}{2}) \cdot b_2.$

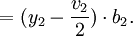
Kritik

Datenreduktion

Der Gini-Koeffizient ist ein statistisches Maß zur Berechnung der Ungleichheitsverteilung. Solche Maße reduzieren prinzipiell einen mehr oder minder komplexeren Datensatz auf eine einfache Kennzahl, die zu Missinterpretationen führen kann, wenn sie nicht sachgemäß verwendet wird. Das gilt nicht nur für die verschiedenen Ungleichheitskoeffizienten, sondern zum Beispiel auch für das Bruttosozialprodukt, bei dessen Berechnung die Information über die einzelnen Beiträge zum Bruttosozialprodukt verloren geht. Die mit aggregierten Maßen erfolgende Datenreduktion hat grundsätzlich Vor- und Nachteile, die bei der Auswertung beachtet werden müssen.

Verschiedene Lorenzkurven - gleicher Gini-Koeffizient

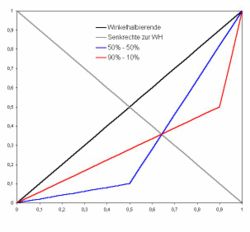
Im Fall des Gini-Koeffizienten gibt es beispielsweise zu jeder Lorenzkurve mindestens eine andere Lorenzkurve mit exakt dem gleichen Gini-Wert. Diese erhält man durch Spiegelung der ursprünglichen Lorenzkurve an der Senkrechten zur Winkelhalbierenden, die durch die Punkte (0,1) und (1,0) verläuft. Ein Beispiel: In einer Volkswirtschaft befindet sich 10% des Eigentums in den Händen von 50% der Bevölkerung, die restlichen 50% besitzen die restlichen 90% (jeweils in den Gruppen gleichverteilt). In einer anderen Volkswirtschaft besitzen 90% der Bevölkerung 50% des Eigentums, während eine Minderheit von 10% die andere Hälfte des Eigentums beansprucht. Die beiden Lorenzkurven sind in der Abbildung dargestellt.

Für die beiden unterschiedlichen Kurven ergibt sich ein gemeinsamer Gini-Koeffizient von 0,4 ^[3]. Das liegt daran, dass ein Repräsentant des reicheren Teils der Bevölkerung in beiden Fällen das 9-fache Eigentum eines Repräsentanten des ärmeren Teils der Bevölkerung besitzt.

Tatsächlich gibt es zu einem Gini-Koeffizienten sogar unendlich viele mögliche Lorenzkurven. In diesem Punkt gleicht der Gini-Koeffizient jeder anderen Kennzahl, die aus der Akkumulation einer größeren Datenmenge abgeleitet ist. Ungleichverteilungskennzahlen wie der Gini-Koeffizient entstehen aus Aggregation von Daten mit der gezielten Absicht, Komplexität zu reduzieren. Der damit einhergehende Informationsverlust ist also keine unbeabsichtigte Nebenwirkung. Für Komplexitätsreduktionen gilt generell, dass sie erst dann zu einem Nachteil werden, wenn man ihr Zustandekommen und ihre Abbildungsfunktion vergisst.

Siehe hierzu auch: Satz von Rothschild & Stiglitz

Fehlerquelle bei Vergleichen

Aussagen, in denen Ungleichheitskoeffizienten miteinander verglichen werden, erfordern eine besonders kritische Überprüfung der Berechnung der einzelnen Koeffizienten. Für einen korrekten Vergleich ist es erforderlich, dass diese Koeffizienten in allen Fällen einheitlich berechnet wurden. Beispielsweise führt die unterschiedliche Granularität der Eingangsdaten zu unterschiedlichen Ergebnissen bei der Berechnung der Ungleichverteilung. Ein mit wenigen Quantilen berechneter Gini-Koeffizient zeigt in der Regel eine etwas geringere Ungleichverteilung an als ein mit mehr Quantilen berechneter Koeffizient, weil im letzteren Fall dank höherer Messauflösung die Ungleichverteilung berücksichtigt werden kann, die innerhalb der Bereiche (d.h. zwischen den Quantilen) im ersten Fall wegen der gröberen Messauflösung unausgewertet bleibt.

Siehe auch

• Tabellenkalkulation für den Gini-Koeffizienten, die Hoover-Ungleichverteilung und den Theil-Index
• Hoover-Ungleichverteilung
• Theil-Index mit einer Grafik, für die aus den Einkommensverteilungen der WIID (World Income Inequality Database, 2007-05) für jede Verteilung der symmetrierte Theil-Index, die Hoover-Ungleichheit und der Gini-Koeffizient berechnet wurden. Über den Gini-Koeffizienten wurden dann die dazugehörigen Differenzen zwischen symmetriertem Theil-Index und der Hoover-Ungleichheit aufgeplottet. Jede dieser Differenzen ist eine mit ihrem eigenen Informationsgehalt gewichtete Ungleichverteilung abzüglich der ungewichteten Ungleichverteilung. Für Gini-Koeffizienten bis 40% sind mit den WIID-Daten die Differenzen meistens negativ.
• Genuine Progress Indicator
• Human Development Index
• Index of Sustainable Economic Welfare
• Wohlfahrtsfunktion
• Liste der Länder nach Einkommensverteilung (nach Gini-Koeffizient)
• Liste der Länder nach Vermögensverteilung (nach Gini-Koeffizient)

Literatur

• AMIEL, Y./COWELL, F.A. 1999: Thinking about inequality, Cambridge.
• Deutsche Bundesbank: Do banks diversify loan portfolios?, 2005 (Anwendung u.A. des Gini-Koeffizienten bei der Risikobewertung von Kredit-Portefolios)
• GINI, C. 1921: Measurement of inequality of income, in: Economic Journal 31, 124-126.
• RAMSER, H.J. 1987: Verteilungstheorie, Berlin.
• SEN, AMARTYA KUMAR: On Economic Inequality (Enlarged Edition with a substantial annexe “On Economic Inequality” after a Quarter Century with James Foster), Oxford 1997, ISBN 0-19-828193-5

Weblinks

• Beschreibung anderer Ungleichverteilungskoeffizienten
• Travis Hale, University of Texas Inequality Project:The Theoretical Basics of Popular Inequality Measures (Theorie mit praktischen Beispielen), Beispiel 1B
• Human Development Report 2004 - Im Anhang („Human Development Indicators“) sind die Gini-Koeffizienten zahlreicher Länder aufgelistet.
• Rechner: on-line und downloadbare Skripte und Macros (für Python, Lua und OpenOffice.org 2.0 Calc)
• Nutzer der freien Datenanalyse-Software R können das Paket „ineq“ von Achim Zeileis installieren, welches eine Reihe von Ungleichheits-Indices berechnen kann (neben Gini auch Atkinson, Theils, RS u.a.m.)
• Verteilung des Weltvermögens (engl.)

Einzelnachweise

1. ↑ SPD-Bundestagsfraktion, Bundestagsdrucksache 13/7828
2. ↑ On-Line-Rechner: Ungleichverteilung
3. ↑ Vergleich: http://www.umverteilung.de/rechner/?quantiles=50,10|50,90 (blaue Kurve) und http://www.umverteilung.de/rechner/?quantiles=90,50|10,50 (rote Kurve)