- Magnetischer Fluß
-
Physikalische Größe Name Magnetischer Fluss Formelzeichen der Größe Φ Größen- und
Einheiten-
systemEinheit Dimension SI Weber (Wb) M·L2/(I·T2) Der Magnetische Fluss (Formelzeichen: Φ) ist eine physikalische Größe zur Beschreibung des magnetischen Feldes. Vergleichbar mit dem elektrischen Strom, ist er die Folge einer magnetischen Spannung und fließt durch einen magnetischen Widerstand. Da selbst das Vakuum einen solchen magnetischen Widerstand darstellt, ist der magnetische Fluss nicht an ein bestimmtes „Medium“ gebunden und wird über Feldgrößen beschrieben.
Inhaltsverzeichnis
Allgemeines
Betrachtet man beispielsweise einen kleinen Zylinder aus einem Material mit gegebener magnetischer Leitfähigkeit, an dem eine magnetische Spannung Um als Folge der magnetischen Feldstärke H und seiner Länge anliegt, so stellt sich ein Strom ein proportional zu seiner Querschnittsfläche. Analog zum elektrischen Widerstand definiert man so den magnetischen Widerstand Rm und kommt zu dem Zusammenhang:
Herrscht beispielsweise im einfachsten linearen, homogenen Fall zwischen den mit den Abstand d zueinander befindlichen Polschuhen eines Magneten die magnetische Feldstärke H, so herrscht entlang der Strecke d die magnetische Spannung:
Durch diese magnetische Spannung bildet sich zwischen den Polschuhen der magnetische Fluss aus. Je nach dem magnetischen Widerstand des zwischen den Polschuhen befindlichen Materials (bzw. des leeres Raumes) stellt sich eine bestimmte Größe des magnetischen Flusses ein. Der magnetische Widerstand ist dabei an die magnetische Leitfähigkeit als Stoff- bzw. Naturkonstante gebunden, so wie ein ohmscher Widerstand an die Stoffkonstante der elektrischen Leitfähigkeit des Widerstandsmaterials gebunden ist.
Im Regelfall arbeitet man in der Feldtheorie nicht direkt mit dem magnetischen Fluss, sondern mit der damit verknüpften magnetischen Flussdichte. Der Grund liegt darin, dass man einen Fluss nur einer bestimmten Fläche im Raum zuordnen kann, nicht aber diskreten Feldpunkten - es existiert keine Funktion Φ(x,y,z) wenn x,y,z Ortskoordinaten bezeichnen. Zeichnerisch wird daher der magnetische Fluss als eine Art „Röhre“ (Flussröhre) dargestellt. Um diese Schwierigkeiten zu vermeiden, wird daher meist mit der vektoriellen Größe der magnetischen Flussdichte gearbeitet. Umgekehrt lässt sich so der magnetische Fluss durch eine Fläche A aus der magnetischen Flussdichte B ableiten als:
Besondere Fälle
- Falls das magnetische Feld homogen, und die Fläche nicht gekrümmt ist, so ist der magnetische Fluss gleich dem Skalarprodukt aus magnetischer Flussdichte B und dem Flächenvektor A (Normalenvektor der Fläche):
- Da das magnetische Feld quellenfrei ist (magnetische Monopole sind nur hypothetische Teilchen) sind die magnetischen Flussdichtelinien immer in sich geschlossen. Dies wird in den Maxwell-Gleichungen ausgedrückt durch:
Daher ist der magnetische Fluss durch eine geschlossene Oberfläche eines Raumsegmentes immer Null, da nach dem Integralsatz von Gauß gilt:
Verkettungsfluss
Als magnetischer Verkettungsfluss wird der gesamte magnetische Fluss einer Induktivität bzw. Spule bezeichnet, der sich durch eine Summation der (nahezu gleich großen) magnetischen Flüsse der einzelnen Leiterschleifen, in die die Wicklung zerlegt werden kann, ergibt.
Maßeinheit
Die Maßeinheit des magnetischen Flusses im SI-Einheitensystem ist Weber, das Einheitenzeichen Wb:
Quantentheorie
Bei der Betrachtung von Quantenphänomenen (z. B. Aharonov-Bohm-Effekt, Quanten-Hall-Effekt) ist das magnetische Flussquantum
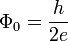 ,
,
also dem Quotient aus dem planckschem Wirkungsquantum und der doppelten Elementarladung eine zweckmäßige Größe. In einigen Supraleitern weist das Flussquantum einen Betrag von
auf [1].
Quellen
- ↑ J. Mannhart, h/e-Periodicity in Superconducting Loops, Nature Physics, VOL 4, 112 (2008), arXiv:0709.4111
Literatur
- Karl Küpfmüller, Gerhard Kohn: Theoretische Elektrotechnik und Elektronik. 14. Auflage. Springer, 1993, ISBN 3-540-56500-0.
Wikimedia Foundation.

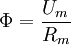
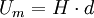
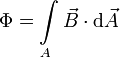
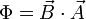
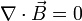
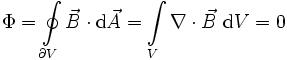
![[\Phi]=\mathrm{T \cdot m^2} = \mathrm{Vs} = \mathrm{Wb}](/pictures/dewiki/49/1bbd58e9c8667c62dfc52fcd175effbc.png)