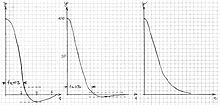
Aperiodischer Grenzfall

Abklingvorgänge bei erlaubtem Fehler von 10%, 3% und 0%. Abklingdauer bei 10%: 2,33 s; bei 3%: 3,27 s; bei 0%: theoretisch unendlich

Der aperiodische Grenzfall beschreibt einen Dämpfungszustand eines harmonischen Oszillators. Es ist die kleinste Dämpfung, bei der die Auslenkung ohne Überschwingen, d.h. einen Richtungswechsel, der Gleichgewichtslage zustrebt, wenn er ohne Anfangsgeschwindigkeit aus einem ausgelenkten Zustand losgelassen wird. Die Annäherung an die Gleichgewichtslage findet in minimal kurzer Zeit statt. Bei noch größerer Dämpfung spricht man vom überaperiodischen Grenzfall oder Kriechfall.

Beispiel: Gedämpfte schwingende Masse

Die Bewegungsgleichung einer gedämpft schwingenden Masse lautet:

$m \ddot{x}+ R \dot{x}+ k x=0$

mit der Auslenkung x, der Dämpfungskonstanten R, der Masse m und der Federkonstanten k.

Üblicherweise identifiziert man $\omega_0 = \sqrt{\frac{k}{m}}$ als die ungedämpfte Eigenkreisfrequenz des harmonischen Oszillators und $\delta = \frac{R}{2 m}$ als die Abklingkonstante, so dass sich für die Bewegungsgleichung eines gedämpften harmonischen Oszillators folgende Form ergibt:

$\ddot{x}+ 2 \; \delta \; \dot{x}+ \omega_0^2 \; x=0$

Diese Gleichung lässt sich mit dem Exponential-Ansatz $x(t) \sim e^{\lambda\cdot t}$ lösen. Es ergibt sich die charakteristische Gleichung:

$\lambda^2 + 2\; \delta \cdot \lambda \;+ \omega_0^2 =0$

Mit der Lösung:

$\lambda_{1,2}=-\delta\pm\sqrt {\delta^2-\omega_0^2}$

Für δ = ω₀ ergibt sich der aperiodische Grenzfall, da dann die Diskriminante dieser Gleichung zu 0 wird. Daher schwingt der Oszillator nicht periodisch, sondern kehrt in minimaler Zeit zur Ruhelage zurück.

Die allgemeine Lösung für den Fall einer doppelten Nullstelle hat dann folgende Form:

$x (t) = x_1 \cdot e^{\lambda \; t} + x_2 \cdot t \cdot e^{\lambda \; t}$

Wird der Schwinger zum Zeitpunkt Null an der Stelle x₁ mit der Geschwindigkeit Null losgelassen, so ergibt sich folgende Gleichung:

$x (t) = x_1 \cdot e^{-\omega_0 \; t}\cdot(1+\omega_0 \; t)$

Dem aperiodischen Grenzfall entspricht eine Lehrsche Dämpfung von D = 1, bzw. ein Gütefaktor von Q = 0,5.