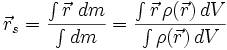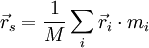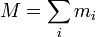Massenmittelpunkt

In der Physik bezeichnet der Massenmittelpunkt den zu einem Körper gehörenden Punkt, auf den sich (gedanklich und rechnerisch) die Masse des Körpers konzentrieren lässt.

Bestimmung

Der Massenmittelpunkt ergibt sich als Mittelwert der Koordinaten 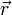$\vec r$ aller Massepunkte dm eines Körpers:

$\vec r_s = \frac{\int \vec r \ dm}{\int dm} = \frac{\int \vec r\, \rho(\vec r) \, dV}{\int \rho(\vec r)\, dV}$

Der Nenner dieser Gleichungen ist die Gesamtmasse M.

Bei diskreten Systemen gilt:

$\vec r_s = \frac{1}{M}\sum_i \vec r_i \cdot m_i$

wobei

$\!\,M=\sum_i m_i$

Bei einem homogenen Körper kann die Dichte ρ herausgekürzt werden, der Massenmittelpunkt fällt dann mit dem Volumenmittelpunkt („geometrischer Schwerpunkt“) zusammen. In vielen Fällen kann die Berechnung vereinfacht werden, wenn man beachtet, dass der Volumenmittelpunkt immer auf den Symmetrieachsen eines Körpers liegt, bei einer Kugel zum Beispiel im Mittelpunkt. Die noch gesuchten Koordinaten ergeben sich dann aus:

$x_s = \frac{1}{V}\int x\, dV\, , \quad y_s = \frac{1}{V}\int y\, dV \, , \quad z_s = \frac{1}{V}\int z\, dV$

Der Massenmittelpunkt gehört zwar zur momentanen Gestalt des Körpers, muss aber selbst kein Teil des Körpers sein: Der Massenmittelpunkt eines Ringes liegt außerhalb des Ringmaterials (nämlich in der Mitte).

Kraftwirkung

Eine am Massenmittelpunkt angreifende Kraft hat die gleiche Wirkung wie die auf alle Massenpunkte des Körpers einwirkende entsprechende Kraftverteilung.

Weiterhin gilt: Ein Körper, auf den eine Kraft im Massenmittelpunkt ausgeübt wird, erfährt dadurch nur eine beschleunigte Translationsbewegung, jedoch keine Winkelbeschleunigung (und damit Drehung).

Massenmittelpunkt und Schwerpunkt

Wenn die Gravitationsfeldstärke über den Bereich des Körpers konstant ist, ist der Massenmittelpunkt identisch mit dem Schwerpunkt. Ist das nicht der Fall, beschreibt der Schwerpunkt den Punkt, in dem die auf den Körper wirkende Schwerkraft zu wirken scheint. Liegt beispielsweise ein (homogener) Ziegelstein auf einem Tisch, so ist dessen untere Hälfte etwas dichter am Erdmittelpunkt als die obere Hälfte. Die untere Hälfte ist deshalb ein ganz klein wenig schwerer als die obere. Der Schwerpunkt liegt damit eine Winzigkeit unterhalb der geometrischen Mitte, die identisch mit dem Massenmittelpunkt ist. Für einen Ziegelstein hat dies natürlich keine praktische Bedeutung; für das Verständnis und für astrophysikalische Zusammenhänge ist die Unterscheidung jedoch wichtig.

Hingegen ist der Massenmittelpunkt jener Punkt, auf den man die Trägheitskräfte des Körpers reduzieren kann. Trägheitseffekte spielen sich deshalb in der Schwerelosigkeit genauso ab wie unter Gravitationswirkung; Rotationen beziehen sich auf den Massenmittelpunkt und nicht auf den Schwerpunkt. Nebenbei: Die drei (Massen-)Trägheitsachsen schneiden sich im Massenmittelpunkt.

Merksätze

• Im homogenen Schwerefeld sind Schwerpunkt und Massenmittelpunkt identisch.
• Für homogene Körper sind Massen- und Volumenmittelpunkt identisch.