- Mathematischer Satz
-
Ein Satz oder Theorem ist in der Mathematik eine im Sinne der Logik widerspruchsfreie Aussage, die mittels eines Beweises als wahr erkannt, das heißt, aus Axiomen und bereits bekannten Sätzen hergeleitet werden kann.
Ein Satz wird nach seiner Rolle, seiner Bedeutung oder seinem Kontext oft auch anders bezeichnet:
- Ein Lemma ist eine Aussage, die als Hilfssatz nur im Beweis anderer Sätze verwendet wird.
- Ein Korollar ist eine triviale Folgerung, die sich aus einem Satz oder einer Definition ohne großen Aufwand ergibt.
- Der Satz im engeren Sinn gibt eine wesentliche Erkenntnis wieder.
Inhaltsverzeichnis
Beispiele für Sätze
Im folgenden sind einige einfache Sätze aufgelistet. Der zu verwendende Kalkül ist in Klammern angegeben.
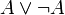 (tertium non datur, Aussagenlogik)
(tertium non datur, Aussagenlogik)- Wenn jeder Mensch sterblich ist und Sokrates ein Mensch ist, dann ist Sokrates sterblich (Prädikatenlogik)
- Jede nicht-leere Menge besitzt mindestens ein Element (Mengenlehre)
- Die Summe der Innenwinkel eines Dreiecks beträgt 180 Grad (Euklidische Geometrie)
- Zu jeder reellen Zahl gibt es eine größere natürliche Zahl (archimedische Ordnung, Analysis)
- Die Quadratwurzel aus zwei ist keine rationale Zahl (Analysis)
- Seien
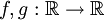 stetig. Dann ist auch
stetig. Dann ist auch 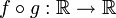 stetig. (Analysis)
stetig. (Analysis)
Aufbau
Formulierung
Obschon ein mathematischer Satz aus einer Aussage beliebiger Form bestehen kann (Beispiel: „Nicht V oder A.“), wird ein mathematischer Satz meist in die im Imperativ formulierte Voraussetzung und die als Aussagesatz formulierte Aussage gegliedert (Beispiel: „Sei V. Es gilt A.“), so dass der Eindruck einer Implikation entsteht.
Besonders im östlichen, deutsch-sprachigen Raum[1] findet sich die folgende Struktur: „Unter der Voraussetzung V gilt die Behauptung(sic!) B.“
Vorsicht: Missverständnis durch die potentiell irreführende Verwendung des Wortes „Behauptung“ ist möglich, obschon eine Behauptung auch umgangssprachlich nicht aus sich allein heraus verständlich wird.
Vorsicht: Fehlschlüsse können entstehen durch das unüberlegte Herauslösen und Anwenden einzelner Teile eines Satzes, da diese im Allgemeinen keine Gültigkeit haben müssen.
Beispiele
- „
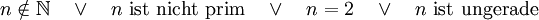 “
“ - „Sei n eine Primzahl. Für n gilt:
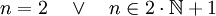 “
“ - „Wenn es regnet, dann wird die Straße nass.“ (kein Satz im mathematischen Sinne)
- Aus der ebenen Geometrie: „Wenn ein echtes Viereck ein Parallelogramm ist, dann haben gegenüberliegende Seiten die gleiche Länge.“ (Hierbei bedeutet „echtes Viereck“, dass ausgeartete und überschlagene Vierecke von der Betrachtung ausgeschlossen sind).
Umkehrsatz
Vertauscht man in einem Satz Voraussetzung und Aussage des Satzes, erhält man den zugehörigen Umkehrsatz. Das sind logische Aussagen der Form „Voraussetzung ⇐ Aussage“. Es sind dann folgende Fälle zu unterscheiden:
- Wenn der Umkehrsatz kein Satz -also falsch- ist, dann ist die Voraussetzung des Satzes hinreichend, aber nicht notwendig.
- Wenn der Umkehrsatz ein Satz -also zutreffend- ist, dann ist die Voraussetzung des Satzes notwendig und hinreichend. In diesem Fall kann man einen weiteren Satz formulieren, in dem Voraussetzung und Aussage des Satzes äquivalent sind (Beispiel: „V gilt, genau dann wenn A gilt“).
Beispiele
- „Wenn die Straße nass ist, dann hat es geregnet.“ Dieser Umkehrsatz ist falsch, denn das Wasser könnte auch anders auf die Straße gekommen sein. Die Voraussetzung des Satzes „es hat geregnet“ ist somit hinreichend, aber nicht notwendig.
- „Wenn in einem echten Viereck gegenüberliegende Seiten die gleiche Länge haben, dann ist es ein Parallelogramm.“ Dieser Umkehrsatz ist wahr. Die Voraussetzung des Satzes ist notwendig und hinreichend. Man kann Satz und Umkehrsatz zusammenfassen: „Ein echtes Viereck ist ein Parallelogramm genau dann, wenn die gegenüberliegenden Seiten die gleiche Länge haben.“
Abhängigkeit von der Aufteilung in Voraussetzung und Aussage
Es ist möglich, dieselbe logische Aussage auf verschiedene Weisen in Voraussetzung und Aussage aufzuteilen, und der Umkehrsatz hängt von dieser Aufteilung ab.
Die logische Aussage
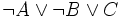 lässt sich zum Beispiel auf die folgenden Weisen als Satz aufschreiben:
lässt sich zum Beispiel auf die folgenden Weisen als Satz aufschreiben: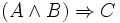 − Umkehrsatz:
− Umkehrsatz: 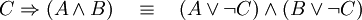
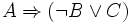 – Umkehrsatz:
– Umkehrsatz: 
Ersichtlich gilt im Allgemeinen nicht, dass die beiden Umkehrsätze äquivalent sind.
Einzelnachweise
- ↑ Informations-Seite der Universität Erlangen: Lehrstuhl für Didaktik der Mathematik
Siehe auch
Wikimedia Foundation.
