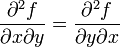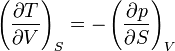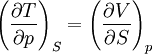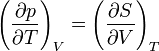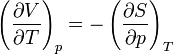Maxwell-Relationen

Die nach dem Physiker James Clerk Maxwell benannten Maxwell-Beziehungen oder Maxwell-Relationen stellen wichtige Zusammenhänge zwischen verschiedenen Größen her.

Thermodynamik

Die maxwellschen Beziehungen der Thermodynamik erlauben es, Änderungen von Zustandsgrößen (z.B. Temperatur T oder Entropie S) als Änderungen anderer Zustandsgrößen (z.B. Druck p oder Volumen V) auszudrücken.

Diese Beziehungen können hergeleitet werden, indem man von den Zustandsfunktionen Innere Energie U, Enthalpie H, Freie Energie F oder Freie Enthalpie G ausgeht und deren totales Differential betrachtet, siehe Charakteristische Funktion (Physik).

Nach dem Satz von Schwarz müssen die gemischten zweiten partiellen Differentialquotienten einer Zustandsfunktion f einander gleich sein:

$\frac{\partial^2 f}{\partial x \partial y} = \frac{\partial^2 f}{\partial y \partial x}$

Wendet man dies auf die vier Zustandsfunktionen U, H, F und G an, erhält man die vier Maxwell-Formeln:

$\left( \frac{\partial T}{\partial V} \right)_S =- \left( \frac{\partial p}{\partial S} \right)_V$

$\left( \frac{\partial T}{\partial p} \right)_S = \left( \frac{\partial V}{\partial S} \right)_p$

$\left( \frac{\partial p}{\partial T} \right)_V = \left( \frac{\partial S}{\partial V} \right)_T$

$\left( \frac{\partial V}{\partial T} \right)_p =- \left( \frac{\partial S}{\partial p} \right)_T$

Guggenheim-Schema

Guggenheim-Quadrat

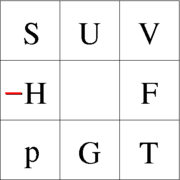
Zum praktischen Arbeiten kann man das sogenannte Guggenheim-Quadrat benutzen. Hieraus erhält man alle oben genannten Maxwell-Relationen.

Man findet die Relation indem man aus den Ecken einer (horizontalen oder vertikalen) Seite des Schemas zwei Variablen abliest, damit eine Seite der Maxwellgleichung formuliert und die andere Seite der Gleichung aus der gegenüberliegenden Seite in gleicher Weise entnimmt.

Zum Beispiel entnimmt man S und p, woraus der Ausdruck dS/dp folgt. Gegenüber liegen dann V und T, was zu dem Ausdruck dV/dT führt. Wenn man auf einer Seite des Gleichheitszeichens S und p stehen hat, ist eine Seite der Relation negativ (in o.g. Beispiel -(dS/dp)=(dV/dT)). Die konstant gehaltene Variable findet sich stets im Nenner der anderen Seite der Relation wieder.

Merksprüche für das Quadrat finden sich unter: Guggenheim-Quadrat#Merksprüche

Elektrodynamik

Die Maxwellsche Beziehung der Elektrodynamik verbindet die Brechzahl n mit der relativen Dielektrizitätskonstante ε_r. Sie ist eine zentrale Gleichung der Elektrodynamik. Im einfachsten Fall lautet sie n ≈ √ε_r

Siehe auch: Maxwellsche Gleichungen