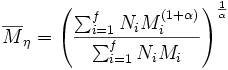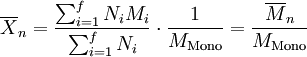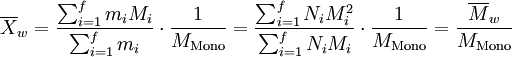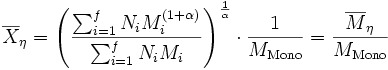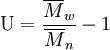Molekulargewichtsverteilung

Die Molmassenverteilung bezeichnet für einen bestimmten Stoff die Verteilung, sprich die anteilsmäßige Aufteilung der molaren Masse der enthaltenen Moleküle. Der Begriff wird sinnvollerweise nur bei Polymeren angewandt, da deren Polymerisationsgrade (und somit auch deren Molmassen) über einen mehr oder weniger breiten Bereich verteilt sind. Bei bestimmten Biopolymeren gibt es nur eine definierte molare Masse. Weitverbreitet ist auch die Bezeichnung Molekulargewichtsverteilung, diese ist aber nicht korrekt (siehe Anmerkung hier).

Verteilungsfunktionen

Entsprechend den Verteilungsfunktionen aus der Mathematik bzw. den physikalisch-chemischen Gegebenheiten bei der Herstellung des Polymers ergeben sich verschiedene mögliche Verteilungsfunktionen:

• Gauss-Verteilung
• Schulz-Zimm-Verteilung
• Poisson-Verteilung

In der Praxis können natürlich auch von diesen theoretischen Modellen abweichende Verteilungen auftauchen. Oft findet man die Bezeichnungen:

• enge Molmassenverteilung

geringe Anzahl von Fraktionen und hohe Anzahl der Moleküle pro Fraktion bzw. relativ wenige und geringe Abweichungen vom Mittelwert, d.h. hohe Einheitlichkeit (meist wünschenswert);

• breite Molmassenverteilung

viele Fraktionen und kleine Anzahl der Moleküle pro Fraktion oder unregelmäßige Verteilung der Moleküle pro Fraktion bzw. relativ viele und hohe Abweichungen vom Mittelwert, d.h. hohe Uneinheitlichkeit (meist unerwünscht).

Molmasse von Polymeren

Typische Molmassenverteilung eines synthetischen Polymers

Es werden verschiedene Mittelwerte definiert, um die Probe statistisch zu beschreiben:

• Zahlenmittel der Molmasse

Die Molmasse M_i des i-mers wird mit dem relativen Zahlenanteil, den dieses Polymer hat, gewichtet.

$\overline {M}_n = \frac {\sum_{i=1}^f N_i M_i } {\sum_{i=1}^f N_i }$ = $\frac{\sum_{i=1}^\infty n_{i} \cdot M_{i} }{\sum_{i=1}^\infty n_{i}} = \sum_{i=1}^\infty x_{i} \cdot M_{i} = \frac{m}{n}$

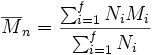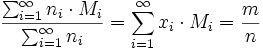
• Gewichtsmittel der Molmasse

Die Molmasse M_i des i-mers wird mit dem relativen Massenanteil, den dieses Polymer hat, gewichtet.

$\overline {M}_w = \frac {\sum_{i=1}^f m_i M_i } {\sum_{i=1}^f m_i } = \frac {\sum_{i=1}^f N_i M_i^2 } {\sum_{i=1}^f N_i M_i }$ = $\frac{\sum_{i=1}^\infty n_{i} \cdot M_{i}^2 }{\sum_{i=1}^\infty n_{i} \cdot M_{i}} = \frac{\sum_{i=1}^\infty x_{i} \cdot M_{i}^2 }{\sum_{i=1}^\infty x_{i} \cdot M_{i}} = \sum_{i=1}^\infty w_{i} \cdot M_{i}$

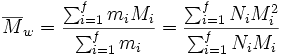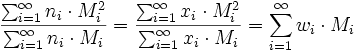
• Zentrifugenmittel der Molmasse (Z-Mittel)

$\overline {M}_z$ = $\frac{\sum_{i=1}^\infty n_{i} \cdot M_{i}^3 }{\sum_{i=1}^\infty n_{i} \cdot M_{i}^2} = \frac{\sum_{i=1}^\infty x_{i} \cdot M_{i}^3 }{\sum_{i=1}^\infty x_{i} \cdot M_{i}^2} = \frac{\sum_{i=1}^\infty w_{i} \cdot M_{i}^2 }{\sum_{i=1}^\infty w_{i} \cdot M_{i}}$

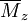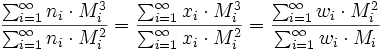
• Viskositätmittel der Molmasse

$\overline {M}_{ \eta } = \left( \frac{\sum_{i=1}^f N_i M_i^{(1+ \alpha)} }{\sum_{i=1}^fN_i M_i} \right)^{\frac{1}{\alpha}}$

α kann Werte zwischen 0 und 1 annehmen.

M_Mono: Molare Masse des Monomers

M_i: Molare Masse der Polymere der jeweiligen Fraktion i

m_i: Gesamtmasse der jeweiligen Fraktion i

N_i: Anzahl der Makromoleküle in der Fraktion i

f: Gesamtanzahl aller Fraktionen

n_i [m_i] = Stoffmenge [Masse] des i-mers; n [m] = Summe aller n_i [m_i]
x_i = Molenbruch des i-mers
M_i = Molmasse des i-mers, M_i = i$\cdot$M₀
M₀ [n₀] = mittlere Molmasse [Stoffmenge] einer monomeren Einheit
w_i = Massenanteil des i-mers
$w_{i} = \frac{m_{i}}{\sum_{i=1}^\infty m_{i}} = x_{i} \cdot \frac{M_{i}}{\bar M_n} = i \cdot x_{i} \cdot \frac{n}{n_0}$

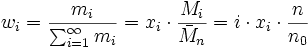
Bestimmungsmethoden

Folgende Analysenmethoden haben sich zur Bestimmung der Molmassenverteilung bewährt:

• Gelpermeations-Chromatografie (GPC)
• Sedimentationsanalyse zur Bestimmung des Zentrifugenmittels
• Massenspektrometrie (MALDI-TOF)
• Viskosimetrie, d. h. rheologisches Verhalten in Lösung
• Rheologie
• Lichtstreuung
• Dampfdruckosmose bei sehr geringen Molmassen (bis ca. 10.000 g/mol)
• Osmometrie bei geringen Molmassen (bis ca. 10.000 g/mol)

Die GPC wird auch zur präparativen Polymerfraktionierung eingesetzt.

Polydispersität

Physikalische, mechanische und rheologische Eigenschaften werden oft durch die Polymolekularität (das Verhältnis von Gewichtsmittel zu Zahlenmittel) bestimmt.
Dieses Verhältnis wird auch Polydispersität Q genannt und ist ein Maß für die Breite einer Molmassenverteilung (MMV). Je größer Q, desto breiter ist die MMV.
$Q = \frac{\overline {M}_w}{\overline {M}_n} \ge 1$
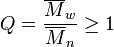
Im Fall, dass Q = 1 ist gilt: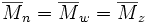 $\overline {M}_n = \overline {M}_w = \overline {M}_z$
Zutreffen wird dieses, wenn die Makromoleküle biologischen Ursprungs sind, z.B. Proteine, Polysaccharide, DNA, die alle die gleiche Molmasse haben.
Für synthetische Polymere hingegen gilt: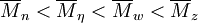

$\overline {M}_n < \overline {M}_{ \eta } < \overline {M}_w < \overline {M}_z$

Das Verhältnis aus Zahlenmittel 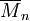$\overline {M}_n$ und der mittleren Molmasse einer monomeren Einheit M₀ gibt den Polymerisationsgrad P_n an. Er beschreibt, wie viele monomere Einheiten zu einem Polymer reagiert haben.
$P_{n} = \frac{\overline {M}_n}{M_0}$

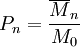
Mittlerer Polymerisationsgrad

Allgemein erhält man den mittleren Polymerisationsgrad durch Division der mittleren molaren Masse durch die molare Masse des Monomeren.

Bei nicht radikalischer Polymerisation muss beachtet werden, ob und welche Gruppen bei der Bindung eines Monomeren abgespalten werden, und dies muss in den Berechnungen berücksichtigt werden.

Ebenso gelten die folgenden Formeln nicht für Copolymerisationen.

Zahlenmittel

$\overline {X}_n = \frac {\sum_{i=1}^f N_i M_i } {\sum_{i=1}^f N_i } \cdot \frac {1} {M_{\mathrm {Mono}}} = \frac { \overline {M}_n } {M_{\mathrm {Mono}}}$

Gewichtsmittel

$\overline {X}_w = \frac {\sum_{i=1}^f m_i M_i } {\sum_{i=1}^f m_i } \cdot \frac {1} {M_{\mathrm {Mono}}} = \frac {\sum_{i=1}^f N_i M_i^2 } {\sum_{i=1}^f N_i M_i } \cdot \frac {1} {M_{\mathrm {Mono}}} = \frac { \overline {M}_w } {M_{\mathrm {Mono}}}$

Viskositätsmittel

$\overline {X}_{ \eta } = \left( \frac{\sum_{i=1}^f N_i M_i^{(1+ \alpha)} }{\sum_{i=1}^fN_i M_i} \right)^{\frac{1}{\alpha}} \cdot \frac {1} {M_{\mathrm {Mono}}} = \frac { \overline {M}_{ \eta }} {M_{\mathrm {Mono}}}$

Molekulare Uneinheitlichkeit

Die molekulare Uneinheitlichkeit U ist ein mathematisches Maß für die Uneinheitlichkeit eines Polymerisats, bzw. für die Breite der Molmassenverteilung.

$\mathrm {U} = \frac {\overline {M}_w} { \overline {M}_n } - 1$

Je kleiner dieser Wert ist, umso einheitlicher ist das Polymerisat, umso enger ist die Molmassenverteilung.

Literatur

• J.M.G. Cowie; Chemie und Physik der synthetischen Polymeren; Vieweg, 2 Ed., 1991.
• K. Matyjaszewski, T.P. Davis; Handbook of Radical Polymerization; Wiley, 2002.
• Bernd Tieke (2000): Makromolekulare Chemie. Eine Einführung Wiley-VCH, Weinheim. ISBN 978-3527293643.