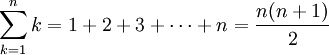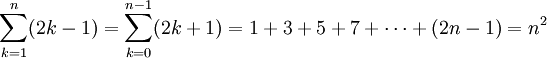Arithmetische Reihe — Arithmetische Reihen sind spezielle mathematische Reihen. Eine arithmetische Reihe ist die Folge, deren Glieder die Summe der ersten n Glieder (den Partialsummen) einer arithmetischen Folge sind. Arithmetische Reihen sind im allgemeinen divergent … Deutsch Wikipedia
Reihen — Reihen, geordnete Folgen von mathematischen Größen (Gliedern), die nach einem gewissen Gesetz gebildet sind. Zu jedem Glied u gehört der Stellenzeiger, d.h. die Zahl, die angibt, das wievielte Glied u in der Reihe ist. Man unterscheidet… … Lexikon der gesamten Technik
Arithmetische Reihe — Arithmetische Reihe, s. Reihen … Meyers Großes Konversations-Lexikon
Arithmetische Reihe — oder Progression der ersten Ordnung ist eine Folge gleichartiger Größen (Glieder der Reihe), deren jede von der vorhergehenden um eine gegebene Größe unterschieden ist; sie heißt steigend oder fallend, je nachdem ihr Unterschied additiv oder… … Herders Conversations-Lexikon
Arithmetische Folge — Eine arithmetische Folge oder arithmetische Progression ist eine regelmäßige mathematische Zahlenfolge mit der Eigenschaft, dass die Differenz zweier benachbarter Folgenglieder konstant ist. Also gilt: (rekursive Formel). Das i te Glied ai einer… … Deutsch Wikipedia
Arithmetische Funktion — Eine zahlentheoretische oder auch arithmetische Funktion ist eine Funktion, die jeder positiven natürlichen Zahl einen Funktionswert aus den komplexen Zahlen zuordnet. Diese Funktionen dienen in der Zahlentheorie dazu, Eigenschaften von… … Deutsch Wikipedia
Dirichlet-Reihen — Dirichletreihen sind Reihen, die in der analytischen Zahlentheorie verwendet werden, um zahlentheoretische Funktionen mit Methoden aus der Analysis, insbesondere der Funktionentheorie zu untersuchen. Viele offene zahlentheoretische… … Deutsch Wikipedia
Formelsammlung Algebra — Die Formelsammlung zur Algebra ist ein Teil der Formelsammlung, in der auch Formeln der anderen Fachbereiche zu finden sind. Inhaltsverzeichnis 1 Grundrechenarten 2 Arithmetische Notation 3 Axiome 4 Elementare Funktionen 4.1 … Deutsch Wikipedia
Endliche Reihe — In der Mathematik ist eine (unendliche) Reihe eine Folge, deren Glieder (Partialsummen) als Summen der ersten n Glieder einer anderen Folge gegeben sind. Inhaltsverzeichnis 1 Nomenklatur 2 Beispiele 3 Konvergenzkriterien 3.1 Beispiele … Deutsch Wikipedia
Partialsumme — In der Mathematik ist eine (unendliche) Reihe eine Folge, deren Glieder (Partialsummen) als Summen der ersten n Glieder einer anderen Folge gegeben sind. Inhaltsverzeichnis 1 Nomenklatur 2 Beispiele 3 Konvergenzkriterien 3.1 Beispiele … Deutsch Wikipedia
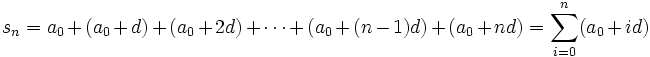 .
.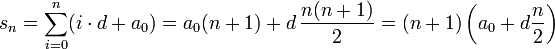 .
.