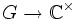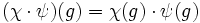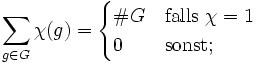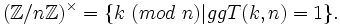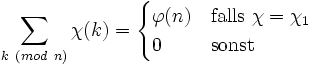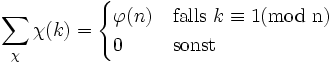Multiplikativer Charakter

Im mathematischen Teilgebiet der Darstellungstheorie sind Charaktere gewisse Homomorphismen.

Charaktere einer Gruppe

Abstrakte und topologische Gruppen

Es sei G eine abstrakte Gruppe oder eine topologische Gruppe. Ein Charakter von G ist ein Gruppenhomomorphismus

$G\to\mathbb C^\times$

in die multiplikative Gruppe der komplexen Zahlen; bei topologischen Gruppen wird noch Stetigkeit gefordert. Ein unitärer Charakter ist ein Charakter, dessen Bild in 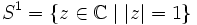$S^1=\{z\in\mathbb C\mid |z|=1\}$ liegt.

Hinweis: Häufig werden allgemeine Charaktere als Quasi-Charaktere und unitäre Charaktere als Charaktere (ohne Zusatz) bezeichnet.

Eigenschaften

• Die Charaktere von G bilden mit der durch

$(\chi\cdot\psi)(g)=\chi(g)\cdot\psi(g)$

erklärten Gruppenverknüpfung eine abelsche Gruppe, die Charakterengruppe.

• Pontrjagin-Dualität: Für lokalkompakte abelsche Gruppen ist die Gruppe der unitären Charaktere mit der Kompakt-offen-Topologie wiederum eine lokalkompakte Gruppe; sie wird auch duale Gruppe 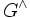$G^\land$ genannt. Die duale Gruppe von 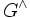$G^\land$ ist auf natürliche Weise zur Ausgangsgruppe G isomorph.

• Die Charaktere von G entsprechen den eindimensionalen komplexen Darstellungen von G, die unitären Charaktere den unitären eindimensionalen Darstellungen.

• Ein Charakter ist genau dann unitär, wenn 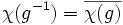$\chi(g^{-1})=\overline{\chi(g)}$ für alle 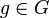$g\in G$ gilt.

• Ist G endlich, so ist jeder Charakter unitär.

• Für einen Charakter χ einer endlichen Gruppe G gilt

$\sum_{g\in G}\chi(g) = \begin{cases} \#G & \mathrm{falls}\ \chi=1 \\ 0 & \mathrm{sonst}; \end{cases}$

dabei steht 1 für den trivialen Charakter mit χ(g) = 1 für alle 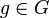$g\in G$. Eine analoge Aussage gilt für kompakte topologische Gruppen; dabei ist die Summe durch ein Integral zu ersetzen.

Dirichlet-Charaktere

In der Zahlentheorie versteht man unter einem Dirichlet-Charakter einen Charakter χ auf der Gruppe

$(\mathbb{Z}/n\mathbb{Z})^{\times} = \{k\ (mod\ n) | ggT(k,n)=1\}.$

Für einen solchen Charakter definiert man eine ebenfalls als Dirichlet-Charakter bezeichnete Funktion

$\chi \colon \mathbb{Z} \to \mathbb{C}$,

$\chi(k) = \begin{cases} \chi(k\ (mod\ n)) & \mathrm{falls} \ ggT(k,n)=1 \\ 0 & \mathrm{falls} \ ggT(k,n)>1 \end{cases}$.

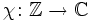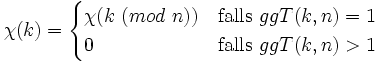Dirichlet-Charaktere spielen eine wichtige Rolle beim Beweis des Dirichletschen Satzes über die Existenz unendlich vieler Primzahlen in arithmetischen Progressionen. Dabei betrachtet man so genannte L-Reihen, das sind Dirichletreihen mit einem Dirichlet-Charakter als Koeffizienten.

Da für endliche abelsche Gruppen die Charaktergruppe isomorph zur Ausgangsgruppe ist, gibt es 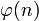$\varphi(n)$ verschiedene Charaktere auf der Gruppe 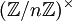$(\mathbb{Z}/n\mathbb{Z})^{\times}$, dabei ist 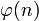$\varphi(n)$ die Eulersche Phi-Funktion.

Für n = 5 ist beispielsweise 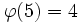$\varphi(5)=4$, d.h. es gibt neben dem Haupt- oder trivialen Charakter χ₁ noch drei weitere Charaktere:

k	1	2	3	4
χ1(k)	1	1	1	1
χ2(k)	1	-1	-1	1
χ3(k)	1	i	-i	-1
χ4(k)	1	-i	i	-1

Für einen Dirichlet-Charakter χ gilt:

$\sum_{k\ (mod\ n)} \chi(k) = \begin{cases} \varphi(n) & \mathrm{falls}\ \chi = \chi_1 \\ 0 & \mathrm{sonst}\end{cases}$

Für ein festes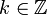 $k \in \mathbb{Z}$ gilt:

$\sum_{\chi} \chi(k) = \begin{cases} \varphi(n) & \mathrm{falls}\ k \equiv 1 \mathrm{(mod\ n)} \\ 0 & \mathrm{sonst}\end{cases}$

wobei die Summe über alle Charaktere 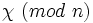$\chi \ (mod\ n)$ genommen wird.

Ein Dirichlet-Charakter ist eine vollständig multiplikative zahlentheoretische Funktion.

Algebraische Gruppen

Ist G eine algebraische Gruppe, so ist ein Charakter von G ein Homomorphismus 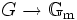$G\to\mathbb G_\mathrm m$; dabei ist 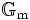$\mathbb G_\mathrm m$ die multiplikative Gruppe. Die Charaktere von G bilden eine (abstrakte) abelsche Gruppe, die mit X(G) oder X ^* (G) bezeichnet wird.

Charaktere von Darstellungen

Ist G eine Gruppe, K ein Körper und ρ eine endlichdimensionale K-lineare Darstellung von G, so heißt die Abbildung

$\chi\colon G\to K,\quad g\mapsto\operatorname{tr}\rho(g),$

die einem Gruppenelement g die Spur des entsprechenden K-linearen Automorphismus ρ(g) zuordnet, der Charakter von ρ. Im eindimensionalen Fall handelt es sich um einen Charakter von G im oben definierten Sinne. Im allgemeinen Fall ist χ jedoch nicht multiplikativ.

Äquivalente Darstellungen haben denselben Charakter. Die Umkehrung – sind zwei Charaktere identisch, so sind auch schon die zugehörigen Darstellungen äquivalent – gilt nicht immer, aber zum Beispiel stets, wenn die Charakteristik des Körpers 0 ist.

Ist K der Körper der komplexen Zahlen und G endlich, so sind die Werte der Charaktere stets endliche Summen von Einheitswurzeln, insbesondere algebraische Zahlen, und es gilt wiederum $\chi(g^{-1})=\overline{\chi(g)}$.

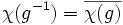Charaktere sind konstant auf Konjugationsklassen. Eine tabellarische Aufstellung der Werte der Charaktere der irreduziblen Darstellungen einer endlichen Gruppe auf den einzelnen Konjugationsklassen nennt man Charaktertafel. Eine praktische Eigenschaft zum Auffinden von irreduziblen Darstellungen sind die Schurschen Orthogonalitätsrelationen für Charaktere.