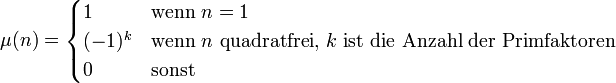Möbius-Funktion

Die Möbiusfunktion μ(n) (auch Möbiussche Müfunktion genannt) ist eine wichtige multiplikative Funktion in der Zahlentheorie und der Kombinatorik. Sie ist nach dem deutschen Mathematiker August Ferdinand Möbius benannt, der sie erstmals im Jahr 1831 eingeführt hat. Diese Funktion ist ein Spezialfall eines allgemeineren Gegenstandes der Kombinatorik.

Definition

μ(n) ist für alle natürlichen Zahlen n definiert und nimmt Werte aus der Menge {-1, 0, 1} an. Dabei hängen die Funktionswerte von der Primfaktorzerlegung von n ab. Die Möbiusfunktion ist wie folgt definiert:

$\mu(n)=\begin{cases}1 & \mbox{wenn } n=1 \\ (-1)^k & \mbox{wenn } n \mbox{ quadratfrei, } k \mbox{ ist die Anzahl der Primfaktoren} \\ 0 & \mbox{sonst} \end{cases}$

Der Funktionswert μ(0) wird im allgemeinen nicht definiert.

Anmerkung: Eine Zahl wird als quadratfrei bezeichnet, wenn sie keinen Teiler hat, der das Quadrat einer natürlichen Zahl ist. Dies ist gleichbedeutend damit, dass die Primfaktorzerlegung nur p-Exponenten mit dem Wert 1 enthält.

Eigenschaften

• Die Möbiusfunktion ist das zur Eins-Funktion inverse Element bezüglich der dirichletschen Faltung.
• Für alle Primzahlen und zusammengesetzte Zahlen mit einer ungeraden Anzahl an teilerfremden Primfaktoren gilt μ(n) = -1.
• Für die summatorische Funktion der Möbiusfunktion gilt für $n \geq 2$:

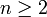∑	μ(d) = 0
d | n

wobei die Summe über alle Teiler von n läuft.

Beispiele

• μ(7) = -1, da 7 eine Primzahl ist.
• μ(66) = (-1)³ = -1, da 66 = 2 · 3 · 11.
• μ(18) = 0, da 18 = 2 · 3 · 3 nicht quadratfrei ist.

Die ersten 20 Werte der μ-Funktion lauten:

n	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
μ(n)	1	-1	-1	0	-1	1	-1	0	0	1	-1	0	-1	1	1	0	-1	0	-1	0

μ(n) = -1	2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 30, 31, ...
μ(n) = 0	4, 8, 9, 12, 16, 18, 20, 24, 25, 27, 28, 32, ...
μ(n) = 1	1, 6, 10, 14, 15, 21, 22, 26, 33, 34, 35, ...

Literatur

• Peter Bundschuh: Einführung in die Zahlentheorie. 5. Auflage. Springer, Berlin 2002, ISBN 3540435794