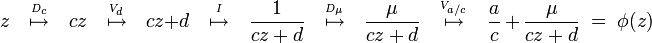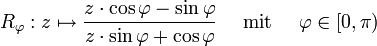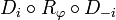- Möbius-Transformation
-
Eine Möbiustransformation, manchmal auch Möbiusabbildung genannt, bezeichnet in der Mathematik eine konforme Abbildung der riemannschen Zahlenkugel auf sich selbst. Sie ist benannt nach August Ferdinand Möbius.
Die allgemeine Formel der Möbiustransformation ist gegeben durch
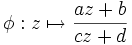 ,
,
wobei a,b,c,d komplexe Zahlen sind, die
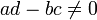 erfüllen.
erfüllen.Inhaltsverzeichnis
Abbildung
Durch die Erweiterung
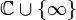 der komplexen Ebene durch einen Punkt im Unendlichen ist die Abbildung unter der riemannschen Zahlenkugel auch für den Wert
der komplexen Ebene durch einen Punkt im Unendlichen ist die Abbildung unter der riemannschen Zahlenkugel auch für den Wert 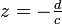 definiert, der auf
definiert, der auf  abgebildet wird.
abgebildet wird.  wiederum wird für
wiederum wird für 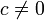 auf
auf  abgebildet, ansonsten auf sich selbst.
abgebildet, ansonsten auf sich selbst.Die Umkehrabbildung ist gegeben durch
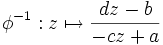 .
.Da mit
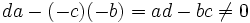 gilt, ist Φ − 1 wiederum eine Möbiustransformation.
gilt, ist Φ − 1 wiederum eine Möbiustransformation.Anwendung findet die Abbildung beispielsweise im Rahmen Signalverarbeitung bei der bilineare Transformation welche einen Bezug in der Systembeschreibung zwischen analogen, kontinuierlichen Systemen und digitalen, diskreten Systemen herstellt.
Elementartypen
Eine Möbiustransformation kann durch eine geeignete Komposition aus Transformationen der folgenden drei Elementartypen gewonnen werden:
- Verschiebung (Translation): Die Verschiebung um den Vektor b wird durch die Abbildung
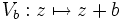 beschrieben.
beschrieben. - Drehstreckung: Mit der komplexen Zahl
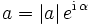 (mit
(mit 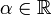 ) beschreibt die Abbildung
) beschreibt die Abbildung 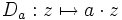 eine Streckung um den Faktor
eine Streckung um den Faktor  kombiniert mit einer Drehung um den Winkel α.
kombiniert mit einer Drehung um den Winkel α. - Inversion: Die Inversion wird durch die Abbildung
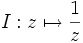 beschrieben. Für ein Gitter lässt sich die Inversion wie folgt veranschaulichen:
beschrieben. Für ein Gitter lässt sich die Inversion wie folgt veranschaulichen:
Die reelle Achse Im(z) = 0 (einschl. des Punktes Unendlich) sowie die imaginäre Achse Re(z) = 0 (ebenso) werden dabei auf sich selbst abgebildet. Die anderen senkrechten und waagerechten Geraden werden in Kreise überführt.
Komposition durch Elementartypen
Eine Möbiustransformation
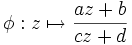 lässt sich nun mittels der Darstellung
lässt sich nun mittels der Darstellung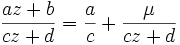 mit
mit 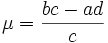
wie folgt aufbauen:
Die Gruppe der Möbiustransformationen
Die Menge aller Möbiustransformation bildet eine Gruppe: Die Hintereinanderausführung zweier Möbiustransformationen ist nämlich wieder eine Möbiustransformation, ebenso ist die inverse Abbildung einer Möbiustransformationen eine solche. Diese Gruppe ist eine Lie-Gruppe und isomorph zur
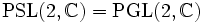 : Jede komplexe 2×2-Matrix mit Determinante ungleich 0 ergibt eine Möbiustransformation, und zwei solche Matrizen stellen genau dann die gleiche Transformation dar, wenn sie komplexe Vielfache voneinander sind. Da
: Jede komplexe 2×2-Matrix mit Determinante ungleich 0 ergibt eine Möbiustransformation, und zwei solche Matrizen stellen genau dann die gleiche Transformation dar, wenn sie komplexe Vielfache voneinander sind. Da 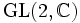 komplex vierdimensional ist und eine Dimension herausgeteilt wird, besitzt die Gruppe der Möbiustransformationen die Dimension 3 über ℂ.
komplex vierdimensional ist und eine Dimension herausgeteilt wird, besitzt die Gruppe der Möbiustransformationen die Dimension 3 über ℂ.Möbiustransformation als Automorphismus der riemannschen Zahlenkugel
Diese Art von Transformationen ist wichtig in der Funktionentheorie, da jede bijektive konforme Abbildung der komplexen Ebene (mit Unendlich) auf sich selbst eine Möbiustransformation ist. Äquivalent dazu ist die Aussage, dass jede bijektive konforme Selbstabbildung der riemannschen Zahlenkugel eine Möbiustransformation ist.
Aus diesem Grund ist die Gruppe der Möbiustransformationen auch genau die Isometriegruppe des 3-dimensionalen hyperbolischen Raums
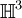 : Dieser besitzt als Rand im Unendlichen die riemannsche Zahlenkugel. Eine Isometrie des hyperbolischen Raumes entspricht eindeutig einer konformen bijektiven Selbstabbildung des Randes im Unendlichen und umgekehrt.
: Dieser besitzt als Rand im Unendlichen die riemannsche Zahlenkugel. Eine Isometrie des hyperbolischen Raumes entspricht eindeutig einer konformen bijektiven Selbstabbildung des Randes im Unendlichen und umgekehrt.Die Beziehung zwischen Rand im Unendlichen und hyperbolischem Raum sieht man am einfachsten im oberen Halbraummodell
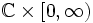 .
.Entsprechend erhält man die Isometrien der hyperbolischen Ebene
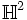 als konforme Abbildungen der kompaktifizierten reellen Geraden
als konforme Abbildungen der kompaktifizierten reellen Geraden 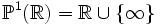 . Dies sind die reellen Möbiustransformationen, die wie oben nur mit
. Dies sind die reellen Möbiustransformationen, die wie oben nur mit 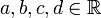 definiert sind.
definiert sind.Transitivitätseigenschaften
Eine Möbiustransformation wird eindeutig dadurch festgelegt, dass man für drei beliebige komplexe Zahlen die Werte der Funktion festlegt.
Die Gruppe der Möbiustransformationen operiert scharf dreifach transitiv auf dem Körper der komplexen Zahlen (mit Unendlich).
Geometrische Eigenschaften
Neben der Konformität der Möbiustransformationen und der Erhaltung des Doppelverhältnisses, ist die Kreisverwandtschaft eine weitere geometrische Invariante, d. h., Kreise auf der riemannschen Zahlenkugel werden unter diesen Abbildungen auf Kreise auf der Sphäre abgebildet; im Allgemeinen jedoch nicht punktweise. Ein interessantes Entscheidungskriterium liefert ein Satz aus der Funktionentheorie: Durch drei verschiedene Punkte der Sphäre verläuft genau eine Kreislinie. Genau dann liegt ein Punkt P auf dieser speziellen Kreislinie, wenn das Doppelverhältnis der vier Punkte reellwertig ist oder den Wert unendlich annimmt. Der Punkt P ist dann und nur dann einer der drei gegebenen, wenn das Doppelverhältnis 0, 1 oder unendlich ist.
Isometrien
Die längenerhaltenden Möbiustransformationen der komplexe Ebene werden durch die elementaren Isometrien Verschiebungen (Translationen) und Drehung gegeben, also durch Dc mit | c | = 1 und Vd, wobei c und d komplexe Zahlen sind.
Die Isometrien auf der riemannschen Zahlenkugel können erzeugt werden durch die π-periodische Rotation
und die Drehung Dc, wieder mit | c | = 1 und c komplex. Die Fixpunkte von R sind i und − i, d. h., R dreht die Zahlenkugel um die durch i und − i gegebene Achse. Die Fixpunkte von D sind 0 und ∞. Durch mehrfache Anwendung können alle Isometrien auf der Zahlenkugel erzeugt werden. Die abstandserhaltenden Rotationen um die durch 1 und –1 gegebene Achse werden zum Beispiel gegeben durch
Die Isometrien haben die Dimension 3 über der reellen Zahlen. Dies gilt sowohl für die Isometrien der Ebene als auch für die Isometrien der Riemannschen Zahlenkugel.
Weblinks
Wikimedia Foundation.