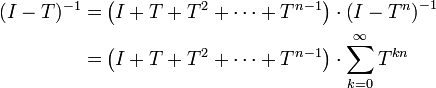Neumannsche Reihe

In der Mathematik ist eine Neumann-Reihe eine Reihe der Form 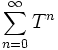$\sum\limits_{n=0}^\infty T^n$, wobei 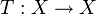$T:X \rightarrow X$ ein stetiger linearer Operator auf einem normierten Raum 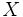$\left.X\right.$ ist und $\left.T\right.^0 := \mathrm{Id}_X$.

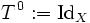Die Reihe entspricht formal einer geometrischen Reihe und ist nach dem Mathematiker Carl Gottfried Neumann benannt, der sie 1877 in der Potentialtheorie verwendete. Sie findet u.a. Anwendung in der Funktionalanalysis zum Lösen von Operatorgleichungen und ist wichtig bei der Untersuchung von stetigen Operatoren, vgl. Spektrum (Operatortheorie).

Eigenschaften

Sei 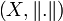$\left(X,\left\|.\right\|\right)$ ein normierter Raum und 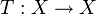$T:X \rightarrow X$ ein stetiger Operator, 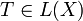$T\in L(X)$. Dabei ist L(X,Y) der Raum der linearen, beschränkten - und somit stetigen - Operatoren von X nach Y; für L(X,X) schreibt man abkürzend L(X).

• Falls die Neumann-Reihe 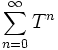$\sum\limits_{n=0}^\infty T^n$ im Raum 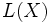$\left.L(X)\right.$ bezüglich der Operatornorm konvergiert, dann ist 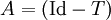$A=\left(\mathrm{Id} - T\right)$ invertierbar und es gilt

$A^{-1}=\left(\mathrm{Id} - T\right)^{-1} = \sum\limits_{k=0}^\infty T^k$.

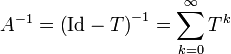• Die Neumann-Reihe konvergiert, falls 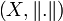$\left(X,\left\|.\right\|\right)$ ein Banachraum ist und für die Operatornorm 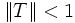$\left\| T \right\| < 1$ gilt. Dann gilt auch:

$\left\| (\mathrm{Id}-T)^{-1}\right\| \leq\left(1-\| T\| \right)^{-1}$.

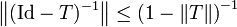• Es sind auch schwächere Voraussetzungen bekannt, unter denen die Reihe konvergieren kann, z. B. ist es ausreichend, wenn nur für eine Potenz des Operators T die Bedingung 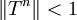$\;\| T^n \| < 1\;$ gilt. Dann ist

$\begin{align} (I-T)^{-1} =&\left(I+T+T^2+\dots+T^{n-1}\right)\cdot \left(I-T^n\right)^{-1}\\ =&\left(I+T+T^2+\dots+T^{n-1}\right)\cdot\sum\limits_{k=0}^\infty T^{kn} \end{align}$

Invertierbarkeit linearer Operatoren

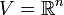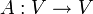Ist V ein Banachraum, z.B. $V=\R^n$ und $A:V\to V$ ein beschränkter Operator, z.B. eine quadratische Matrix 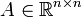$A\in\R^{n\times n}$, so kann A für jeden Skalierungsfaktor γ > 0 als

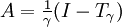$A=\tfrac1\gamma(I-T_\gamma)\;$ mit $\;T_\gamma=I-\gamma\,A$

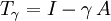
dargestellt werden.

Gibt es nun einen Skalierungsfaktor, mit welchem 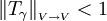$\|T_\gamma\|_{{}_{V\to V}}<1$ in der induzierten Operatornorm gilt, so ist A invertierbar und die Inverse ist, unter Benutzung der Neumannreihe,

$A^{-1}=\gamma\left(I+\sum_{k=1}^\infty T_\gamma{}^k\right) =\gamma\left(I+\sum_{k=1}^\infty (I-\gamma\,A)^k\right)$.

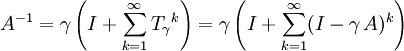Offenheit der Menge der invertierbaren Operatoren

Seien B,B' zwei Banachräume und 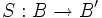$S:B\to B'$ ein invertierbarer Operator. Dann gilt für jeden weiteren Operator $T:B\to B'$:

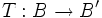Gilt für den Abstand in der Operatornorm von S zu T die Abschätzung 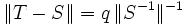$\|T-S\|=q\,\|S^{-1}\|^{-1}$ mit 0 < q < 1, so ist T ebenfalls invertierbar und die Inverse hat die Operatornorm

$\|T^{-1}\|\le\tfrac1{1-q}\|S^{-1}\|$.

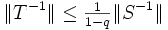Zum Beweis: Es wird T = S(I − (I − S ^{− 1}T)) zerlegt und auf den zweiten Faktor die Neumann-Reihe angewandt. Die Konvergenz ist gesichert, denn nach Voraussetzung gilt:

$\|I-S^{-1}T\|\le\|S^{-1}\|\,\|S-T\|\le q&amp;lt;1$.

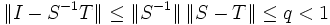Als Folge ergibt sich, dass die Menge der invertierbaren Operatoren offen ist bzgl. der Topologie der Operatornorm.

Literatur

• Dirk Werner: Funktionalanalysis. Springer Verlag, 2005. ISBN 3-540-43586-7