Operatorgleichung

Die Funktionalanalysis ist der Zweig der Mathematik, der sich mit der Untersuchung von Vektorräumen und stetigen Abbildungen auf solchen befasst. Hierbei werden Analysis, Topologie und Algebra verknüpft. Ziel dieser Untersuchungen ist es, abstrakte Aussagen zu finden, die sich auf verschiedenartige konkrete Probleme anwenden lassen.

Von zentraler Bedeutung sind die Begriffe

• Funktional für eine Abbildung von Vektoren (z. B. Funktionen) auf skalare Größen und
• Operator für eine Abbildung von Vektoren auf Vektoren. (Der Begriff des Operators ist eigentlich viel allgemeiner. Sinnvollerweise betrachtet man sie jedoch auf algebraisch und topologisch strukturierten Räumen, wie z. B. topologischen / metrischen / normierten Vektorräumen aller Art.)

Beispiele:

• Funktional: Folgengrenzwert, Norm, bestimmtes Integral
• Operator: Differentiation, unbestimmtes Integral, Faltung, Shift-Operatoren für Folgen

Grundbegriffe der Analysis wie Stetigkeit, Ableitungen usw. werden in der Funktionalanalysis auf Funktionale und Operatoren erweitert. Gleichzeitig weitet man die Resultate der linearen Algebra (beispielsweise den Spektralsatz) auf topologisch lineare Räume (beispielsweise den Hilbertraum) aus, was mit sehr bedeutsamen Ergebnissen verbunden ist.

Die historischen Wurzeln der Funktionalanalysis liegen im Studium der Fourier-Transformation (und ähnlicher Transformationen) und der Untersuchung von Differential- und Integralgleichungen. Der Wortbestandteil „funktional“ geht zurück auf die Variationsrechnung. Als Begründer der modernen Funktionalanalysis gelten Stefan Banach, Frigyes Riesz und Maurice René Fréchet.

Topologische Vektorräume

Grundlage der Funktionalanalysis sind Vektorräume über den reellen oder komplexen Zahlen. Der Grundbegriff ist hier der topologische Vektorraum, etwas konkreter werden auch lokal konvexe topologische Vektorräume und Fréchet-Räume untersucht. Wichtige Aussagen sind dabei der Satz von Hahn-Banach, der Satz von Baire und der Satz von Banach-Steinhaus. Insbesondere in der Lösungstheorie partieller Differentialgleichungen spielen diese eine wichtige Rolle, darüber hinaus in der Fredholm-Theorie.

Normierte Räume

Der wichtigste Spezialfall lokalkonvexer topologischer Vektorräume sind normierte Vektorräume. Sind diese zusätzlich vollständig, dann heißen sie Banachräume. Noch spezieller betrachtet man Hilberträume, bei denen die Norm von einem Skalarprodukt erzeugt wird. Diese Räume sind von grundlegender Bedeutung für die mathematische Formulierung der Quantenmechanik. Ein wichtiger Untersuchungsgegenstand sind stetige lineare Operatoren auf Banach- oder Hilbert-Räumen.

Hilberträume können vollständig klassifiziert werden: Für jede Mächtigkeit einer Basis existiert (bis auf Isomorphie) genau ein Hilbertraum zu einem Körper. Da endlich-dimensionale Hilberträume von der linearen Algebra erfasst werden und jeder Morphismus zwischen Hilberträumen in Morphismen von Hilberträumen der Dimension $\aleph_0$ (Aleph Null, siehe Mächtigkeit und Abzählbarkeit) zerlegt werden kann, betrachtet man in der Funktionalanalysis hauptsächlich den Hilbertraum der Dimension $\aleph_0$ und seine Morphismen. 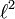Dies ist der Raum $\ell^2$ aller Folgen mit der Eigenschaft, dass die Summe der Quadrate aller Folgenglieder endlich ist.

Banachräume sind dagegen viel komplexer. Es gibt zum Beispiel keine praktisch nutzbare allgemeine Definition einer Basis (z. B. ist eine Basis vom unter Basis (Vektorraum) beschriebenen Typ (auch Hamelbasis genannt) hier meist nicht-konstruktiv, lässt sich also nicht explizit angeben).

Für jede reelle Zahl 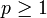$p \geq 1$ gibt es den Banachraum „aller Lebesgue-messbaren Funktionen, deren p-te Potenz des Betrags ein endliches Integral hat“ (siehe Lp-Raum).

Beim Studium normierter Räume ist die Untersuchung des Dualraumes wichtig. Der Dualraum besteht aus allen stetigen linearen Funktionen vom normierten Raum in seinen Skalarkörper, also in die reellen oder komplexen Zahlen. Der Bidual, also der Dualraum des Dualraums, muss nicht isomorph zum ursprünglichen Raum sein, aber es gibt stets einen natürlichen Monomorphismus von einem Raum in seinen Bidual. Ist dieser spezielle Monomorphismus auch surjektiv, dann spricht man von einem reflexiven Banachraum.

Der Begriff der Ableitung lässt sich auf Funktionen zwischen Banachräumen so verallgemeinern, dass die Ableitung in einem Punkt eine stetige lineare Abbildung ist.

Literatur

• Hans Wilhelm Alt: Lineare Funktionalanalysis : eine anwendungsorientierte Einführung. 5. Auflage. Springer-Verlag, 2006, ISBN 3-540-34186-2
• Haïm Brezis: Analyse fonctionnelle : théorie et applications. In: Mathématiques appliquées pour la maîtrise. Dunod, 2005, ISBN 2-10-049336-1
• Nelson Dunford, Jacob Theodore Schwartz u. a.: Linear Operators, General Theory, and other 3 volumes, includes visualization charts. In: Pure and applied mathematics; 7. Wiley-Interscience, 1988, ISBN 0-47-022605-6
• Harro Heuser: Funktionalanalysis: Theorie und Anwendung. 3. Auflage. Teubner-Verlag, 1992, ISBN 3-519-22206-X
• Vivien Hutson, John S. Pym, Michael J. Cloud: Applications of Functional Analysis and Operator Theory. 2nd edition. Elsevier Science, 2005, ISBN 0444517901
• Leonid P. Lebedev, Iosif I. Vorovič: Functional Analysis in Mechanics. Springer-Verlag, 2003, ISBN 0-387-95519-4
• Martin Schechter: Principles of Functional Analysis. 2nd edition. Academic Press, 2001, ISBN 0-8218-2895-9
• Sergej Lʹvovič Sobolev: Some applications of functional analysis in mathematical physics, Providence (RI), American Mathematical Soc., 1991, ISBN 0-8218-4549-7
• Dirk Werner: Funktionalanalysis, 6. Auflage, Springer-Verlag 2007, ISBN 978-3-540-72533-6
• Kôsaku Yosida: Functional Analysis. 6th edition. Springer-Verlag, 1980, ISBN 3-540-10210-8

Die Bücher Alt (2006) und Heuser (1992) bieten eine Einführung und einen ersten Überblick über „klassische“ Sätze der Funktionalanalysis. Dabei wird als roter Faden immer wieder auf physikalische Anwendungen eingegangen. Heuser hat zu jedem Kapitel Übungsaufgaben, für die zum größten Teil im Anhang eine Lösung skizziert wird. Das letzte Kapitel „Ein Blick auf die werdende Analysis“ beschreibt die wichtigsten Schritte der historischen Entwicklung zur heutigen Funktionalanalysis.