Offenes Intervall

Ein Intervall ist eine „zusammenhängende“ Teilmenge einer geordneten Menge. Dabei bedeutet „zusammenhängend“: Wenn zwei Objekte in der Teilmenge enthalten sind, dann sind auch alle Objekte, die dazwischen liegen, darin enthalten. In der Regel betrachtet man die Menge der reellen Zahlen, manchmal auch die der rationalen, der ganzen oder der natürlichen Zahlen.

Beispiele

In den natürlichen Zahlen

{5,6,7,8,9}

In diesem Fall einer diskreten Menge sind die Elemente des Intervalls benachbart.

In der Menge der reellen Zahlen

$[0,1] = \{x \in \R \;|\; 0 \le x \le 1\}$,

die Menge aller Zahlen zwischen 0 und 1, wobei die Endpunkte 0 und 1 mit eingeschlossen sind.

Triviale Beispiele von Intervallen sind die leere Menge und Mengen, die genau ein Element besitzen. Wenn man diese nicht einschließen möchte, dann spricht man von echten Intervallen.

Die Menge {5,6,7,8,9} kann auch als Menge von reellen Zahlen betrachtet werden. In diesem Fall handelt es sich nicht um ein Intervall, da die Menge zum Beispiel die zwischen 6 und 7 liegenden Bruchzahlen nicht enthält.

Bezeichnungs- und Schreibweisen

Ein Intervall kann (beidseitig) beschränkt sein oder (einseitig) unbeschränkt. Es ist durch seine untere und seine obere Intervallgrenze eindeutig bestimmt, wenn zusätzlich angegeben wird, ob diese Grenzen im Intervall enthalten sind. Ein Intervall heißt abgeschlossen, wenn es beide Grenzen enthält, und offen, wenn die beiden Grenzen nicht enthalten sind. Ein Intervall heißt halboffen, wenn es genau eine der beiden Intervallgrenzen enthält. In mancher Literatur werden beschränkte Intervalle auch als eigentlich, unbeschränkte als uneigentlich bezeichnet.

Es gibt zwei verschiedene häufig verwendete Intervallschreibweisen. Bei einer der beiden verwendet man für ein offenes Ende runde und für ein geschlossenes Ende eckige Klammern. Bei der anderen Schreibweise werden geschlossene Enden ebenfalls durch eckige Klammern gekennzeichnet, offene Enden dagegen durch gespiegelte eckige Klammern. Im Folgenden werden beide Schreibweisen verwendet und der Mengenschreibweise gegenübergestellt:

Beschränkte Intervalle

abgeschlossenes Intervall

$[a,b] := \{x\in\R \,|\, a\le x \le b\}$

Das Intervall enthält sowohl a als auch b. Ein abgeschlossenes und beschränktes Intervall heißt auch kompaktes Intervall.

offenes Intervall

$(a,b) = {]a,b[} := \{x \in\R \,|\, a<x<b\}$

Das Intervall enthält weder a noch b.

halboffenes (genauer rechtsoffenes) Intervall

$[a,b) = {[a,b[} := \{x \in\R \,|\, a \le x<b\}$

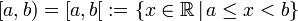
Das Intervall enthält a, aber nicht b.

halboffenes (genauer linksoffenes) Intervall

$(a,b] = {]a,b]} := \{x \in\R \,|\, a < x \le b\}$

Das Intervall enthält nicht a, wohl aber b.

Unbeschränkte Intervalle

Einseitig unbeschränkte Intervalle besitzen auf der unbeschränkten Seite keine Endpunkte. Man schreibt stattdessen die Symbole 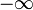$-\infty$ und $\infty$, die (auch bei abgeschlossenen unbeschränkten Intervallen) immer ausgenommen sind.

linksseitig unendliches abgeschlossenes Intervall

$({-\infty}, b] = {]{-\infty}, b]} := \{x \in \R \,|\, x \le b\}$

Es enthält alle Zahlen die kleiner oder gleich b sind.

linksseitig unendliches offenes Intervall

$({-\infty}, b) = {]{-\infty}, b[} := \{x \in \R \,|\, x < b\}$

Es enthält alle Zahlen die kleiner als b sind.

rechtsseitig unendliches abgeschlossenes Intervall

$[a, \infty) = {[a,{\infty}[} := \{x \in \R \,|\, a \le x\}$.

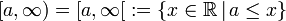Es enthält alle Zahlen, die größer oder gleich a sind.

rechtsseitig unendliches offenes Intervall

$(a, \infty) = {]a,{\infty}[} := \{x \in \R \,|\, a < x\}$.

Es enthält alle Zahlen, die größer als a sind.

Bei obiger Definition wird übrigens nicht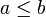 $a\leq b$ gefordert, sodass für a > b jedes Intervall leer ist. Daneben existieren auch je nach Anwendung Definitionen, die solche Intervalle nicht erlauben oder im Falle a > b einfach die Grenzen vertauschen.

Zur Vermeidung von Verwechslungen mit dem Dezimalkomma wird als Trennzeichen auch das Semikolon (;), selten auch ein senkrechter Strich (|) verwendet, z. B.

$(0, 2{,}5] = (0; 2{,}5] = (0|2{,}5].\,$

Verallgemeinerung

In der Topologie sind reelle Intervalle Beispiele für zusammenhängende Mengen. Offene Intervalle sind offene Mengen und abgeschlossene Intervalle sind abgeschlossene Mengen. Halboffene Mengen sind weder offen noch abgeschlossen. Abgeschlossene beschränkte Intervalle sind kompakt.

Alle hier für die reellen Zahlen $\mathbb{R}$ gemachten Schreibweisen lassen sich direkt auf beliebige total geordnete Mengen übertragen.

Siehe auch

• Intervallschachtelung
• Intervallarithmetik
• Äquidistanz (Mathematik)