Orthozentrum

Höhenschnittpunkt

Der Höhenschnittpunkt (auch: Orthozentrum) eines Dreiecks ist der Schnittpunkt seiner drei Höhen, d.h. der Lote zu den Dreiecksseiten durch die gegenüberliegenden Ecken. Der Höhenschnittpunkt ist einer der vier klassischen ausgezeichneten Punkte des Dreiecks.

In der Skizze sind die Höhen mit [AH_a], [BH_b] und [CH_c] bezeichnet. Ist das gegebene Dreieck ABC spitzwinklig, so befindet sich der Höhenschnittpunkt H innerhalb des Dreiecks. Hat das Dreieck dagegen einen stumpfen Winkel (also einen Winkel über 90°), so liegt H außerhalb. Im rechtwinkligen Fall schließlich stimmt H mit dem Scheitel des rechten Winkels überein.

Beweis

Dreieck mit Höhen und Parallelen zu den Seiten

Zum Beweis, dass sich alle drei Höhen des Dreiecks ABC in einem Punkt schneiden, zeichnet man die Parallelen zu den Dreiecksseiten durch die gegenüberliegenden Ecken, sodass ein größeres Dreieck A'B'C' entsteht. Je zwei der vier Teildreiecke des neuen Dreiecks bilden ein Parallelogramm. In einem Parallelogramm sind gegenüberliegende Seiten gleich lang. Daher sind die Seiten des neuen Dreiecks doppelt so lang wie die entsprechenden Seiten des ursprünglichen Dreiecks. Die Höhen des ursprünglichen Dreiecks stimmen daher mit den Mittelsenkrechten (Streckensymmetralen) des neuen Dreiecks überein. Da sich die Mittelsenkrechten eines Dreiecks in einem Punkt schneiden, muss dies auch für die Höhen des Ausgangsdreiecks gelten.

Eigenschaften

• Das Dreieck aus den Fußpunkten H_a, H_b und H_c der Höhen bezeichnet man als das Höhenfußpunktdreieck des Dreiecks ABC. Ist das Dreieck ABC spitzwinklig, dann ist der Höhenschnittpunkt H des Dreiecks ABC der Inkreismittelpunkt des Höhenfußpunktdreiecks; ist das Dreieck ABC stumpfwinklig, dann ist der Höhenschnittpunkt H des Dreiecks ABC ein Ankreismittelpunkt des Höhenfußpunktdreiecks.

• Die Produkte der Höhenabschnitte sind gleich:

$\overline{AH} \cdot \overline{HH_{a}}= \overline{BH} \cdot \overline{HH_{b}} = \overline{CH} \cdot \overline{HH_{c}}$.

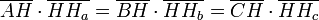• Der Höhenschnittpunkt liegt - wie der Schwerpunkt und der Umkreismittelpunkt - auf der eulerschen Geraden.

• Die Fußpunkte der Höhen und die Mittelpunkte der "oberen Höhenabschnitte" (jeweils zwischen dem Höhenschnittpunkt und einer Ecke) liegen auf dem Feuerbach-Kreis.

• Spiegelt man den Höhenschnittpunkt an den drei Seiten des Dreiecks, so liegen die Bildpunkte auf dem Umkreis.

Koordinaten

Höhenschnittpunkt eines Dreiecks (Orthozentrum, X4)
Trilineare Koordinaten	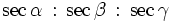$\sec\alpha \, : \, \sec\beta \, : \, \sec\gamma$
Baryzentrische Koordinaten	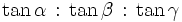$\tan\alpha \, : \, \tan\beta \, : \, \tan\gamma$

Literatur

• H. Schupp: Elementargeometrie. UTB Schöningh 1977, ISBN 3-506-99189-2, S.50

Weblinks

• http://www.uni-flensburg.de/mathe/zero/fgalerie/trianglecenters/x4.html interaktives Java-Applet, das die Höhen und den Höhenschnittpunkt anzeigt
• http://www.mathe-werkstatt.de/titel.htm interaktives Java-Applet, das die Kurve der Höhenschnittpunkte anzeigt