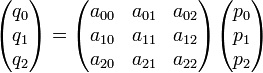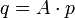Projektive Transformationen
- Projektive Transformationen
-
Eine kollineare Abbildung (oder: Projektive Abbildung, Projektive Transformation), auch Kollineation, ist eine bijektive Abbildung zwischen projektiven Ebenen bzw. Räumen, die alle Geraden wieder auf Geraden abbildet. Dabei werden Vierecke, insbes. also Quadrate, auf allgemeine Vierecke abgebildet.
Spezialfälle der kollinearen Abbildung sind die affinen Abbildungen. Eine Kollineation einer affinen Inzidenzebene ist eine bijektive Abbildung, bei der Punkte auf Punkte und Geraden auf Geraden bei Inzidenzerhalt abgebildet werden und bei der die Parallelität von Geraden invariant ist, d. h. erhalten bleibt. Quadrate werden also auf Parallelogramme abgebildet.
Ein weiterer Spezialfall ist die geometrische Bewegung, oder auch die Ähnlichkeitsabbildung, bei der Quadrate auf Quadrate abgebildet werden.
Eine kollineare Abbildung einer klassischen projektiven Ebene auf sich kann unter Verwendung homogener Koordinaten aus einem Körper K als Matrix-Vektor-Produkt geschrieben werden.
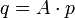
oder in den einzelnen Koordinaten:
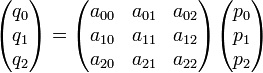
dabei sind p und q Elemente des dreidimensionalen Vektorraumes über K, und p0,p1,p2 oder q0,q1,q2 homogene Koordinaten (oder projektive Koordinaten) eines Punktes in der Ebene. Die zugehörigen kartesischen Koordinaten sind über

gegeben. Die obige Matrix muss nichtsingulär (invertierbar) sein, d. h. ihre Determinante ist nicht Null.
Ein typisches Beispiel für eine kollineare Abbildung ist die Zentralprojektion einer Ebene auf eine andere in einem projektiven Raum.
Besonders wichtige Kollineationen sind die zentralen Kollineationen. Diese bilden jede Gerade durch einen festen Punkt Z (das Zentrum) auf sich ab. Sie lassen im Fall der Ebene alle Punkte einer Geraden (der Achse) und im Fall des Raumes alle Punkte einer Ebene bzw. Hyperebene (wieder Achse genannt) einzeln fest. Wenn das Zentrum auf der Achse liegt, spricht man von einer Elation, anderenfalls von einer Homologie (das hat nichts mit dem Homologiebegiff der Topologie zu tun).
Siehe auch
Wikimedia Foundation.
Schlagen Sie auch in anderen Wörterbüchern nach:
projektive Geometrie — projektive Geometrie, Teilgebiet der Geometrie. Bei der Projektion einer Ebene E auf eine Ebene E durch Sehstrahlen von einem Augenpunkt Z aus entsprechen denjenigen Punkten P auf E, deren Sehstrahlen ZP der Ebene … Universal-Lexikon
Projektive lineare Gruppe — Allgemeine lineare Gruppe GL(n,K) berührt die Spezialgebiete Mathematik Gruppentheorie Lie Gruppen Physik Symmetrie Quantenmechanik Eichtheorie Relativitätstheorie Lorentz Gruppe … Deutsch Wikipedia
7-Parameter-Transformation — Die Helmert Transformation (nach Friedrich Robert Helmert, 1843 1917; auch: 7 Parameter Transformation) ist eine Koordinatentransformation für dreidimensionale kartesische Koordinaten, die in der Geodäsie häufig zur verzerrungsfreien Umrechnung… … Deutsch Wikipedia
Sieben-Parameter-Transformation — Die Helmert Transformation (nach Friedrich Robert Helmert, 1843 1917; auch: 7 Parameter Transformation) ist eine Koordinatentransformation für dreidimensionale kartesische Koordinaten, die in der Geodäsie häufig zur verzerrungsfreien Umrechnung… … Deutsch Wikipedia
Funktionaltransformation — Die Mathematik versteht unter einer Transformation eine Art Abbildung. Die Verwendung dieses Wortes lässt sich grob in drei Bereiche unterteilen: Koordinatentransformationen und Abbildungen, die mit gewissen geometrischen Eigenschaften kompatibel … Deutsch Wikipedia
Helmert-Transformation — Die Helmert Transformation (nach Friedrich Robert Helmert, 1843 1917), auch 7 Parameter Transformation genannt, ist eine Koordinatentransformation für dreidimensionale kartesische Koordinaten, die in der Geodäsie häufig zur verzerrungsfreien… … Deutsch Wikipedia
Transformation (Mathematik) — Die Mathematik versteht unter einer Transformation eine Art Abbildung. Die Verwendung dieses Wortes lässt sich grob in drei Bereiche unterteilen: Koordinatentransformationen und Abbildungen, die mit gewissen geometrischen Eigenschaften kompatibel … Deutsch Wikipedia
NURBS — Fläche (grün) vom Grad 4, definiert durch 36 Kontrollpunkte (rot) über einem zweidimensionalen Parametergebiet (unteres Gitter). Non Uniform Rational B Splines (deutsch: Nicht uniforme rationale B Splines, kurz NURBS) sind mathematisch definierte … Deutsch Wikipedia
Non-Uniform Rational B-Spline — Dreidimensionale NURBS Flächen können komplexe, organische Formen aufweisen. Kontrollpunkte beeinflussen die Richtungen der Oberfläche. Das äußerste Quadrat unten skizziert die X/Y Ausdehnungen der Oberfläche … Deutsch Wikipedia
Nurbs — Fläche (grün) vom Grad 4, definiert durch 36 Kontrollpunkte (rot) über einem zweidimensionalen Parametergebiet (unteres Gitter). Non Uniform Rational B Splines (deutsch: Nicht uniforme rationale B Splines, kurz NURBS) sind mathematisch definierte … Deutsch Wikipedia