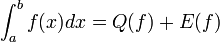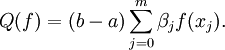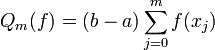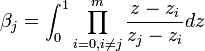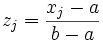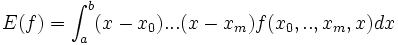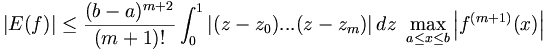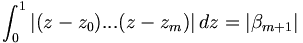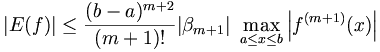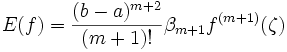Quadraturformel

Numerische Integration sucht einfache Approximationen des Wertes S

In der numerischen Mathematik bezeichnet numerische Quadratur bzw. numerische Integration die näherungsweise Berechnung von Integralen. Oft kann man Integrale nicht geschlossen lösen, d. h. man kann keine Stammfunktion zu f angeben oder die Funktion ist nur durch diskrete Werte, etwa Messungen, gegeben. Dann versucht man, Näherungswerte zu ermitteln.

Man bezeichnet mit

$\int_{a}^{b}f(x)dx= Q(f) + E(f)$

das Integral der Funktion f(x) im Intervall [a,b]. Dies wird hier dargestellt als der Wert einer Quadraturformel Q(f) plus dem Fehler E(f). Eine allgemeine Quadraturformel besteht dabei aus einer Summe von m+1 Funktionswerten, multipliziert mit Gewichten β_j:

$Q(f) = (b-a)\sum_{j=0}^m \beta_j f(x_j).$

Die Punkte x₀,...x_m heißen Stützstellen . Je nach Wahl der Stützstellen und Gewichte ist die Näherung besser oder schlechter, der Fehler wird durch das Restglied E(f) beschrieben. Ebenso wie das Integral sind Quadraturformeln lineare Operatoren.

Interpolatorische Quadraturformel

Eine wichtige Klasse von Quadraturformeln ergibt sich durch die Idee, die Funktion f(x) durch ein Interpolationspolynom vom Grad m zu approximieren und dieses dann zu integrieren. Die Gewichte ergeben sich dann als die Integrale der Lagrange-Polynome zu den gegebenen Stützstellen. Nach Konstruktion werden Polynome vom Grad m exakt integriert. Die Quadraturformel lautet also

$Q_m(f) = (b-a)\sum_{j=0}^m f(x_j)$

mit den Koeffizienten

$\beta_j=\int_0^1 \prod_{i=0, i\neq j}^m\frac{z-z_i}{z_j-z_i} dz$

$z_j = \frac{x_j -a}{b-a}$

Werden die Stützstellen äquidistant gewählt, ergeben sich die Newton-Cotes-Formeln. Werden auf jedenfall die Integrationsränder als Stützstellen gewählt, ergeben sich die abgeschlossenen Newton-Cotes-Formeln. Zu diesen gehören unter anderem die Trapezregel und die Simpson-Regel. Die abgeschlossenen Newton-Cotes-Formeln von geradem Grad integrieren sogar Polynome von einem Grad höher exakt.

Fehlerabschätzung

Das Restglied beträgt

$E(f) = \int_a^b(x-x_0)...(x-x_m)f(x_0,..,x_m,x)dx$

mit der dividierten Differenz f(x₀,..,x_m,x). Ist die Funktion f im Intervall [a,b] (m + 1)-mal stetig differenzierbar („reellwertig“ wird nicht gefordert), dann lässt sich das Restglied nach oben abschätzen durch

$\left| E(f) \right| \le {(b-a)^{m+2} \over (m+1)!}\int_{0}^{1}{\left|(z-z_0)...(z-z_m)\right|dz}\ \max_{a\le x \le b} {\left| f^{(m+1)}(x) \right|}$

Wenn noch zusätzlich für alle Stützstellen im Intervall [a,b] gilt 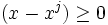$(x-x^j)\geq0$ oder alternativ 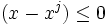$(x-x^j)\leq 0$, dann hat der Integrand keinen Vorzeichenwechsel in [a,b] und man kann zeigen:

$\int_{0}^{1}{\left|(z-z_0)...(z-z_m)\right|dz} = {\left|\beta_{m+1} \right|}$

Daraus folgt dann die Restgliedabschätzung

$\left| E(f) \right| \le {(b-a)^{m+2} \over (m+1)!}{\left|\beta_{m+1} \right|}\ \max_{a\le x \le b} {\left| f^{(m+1)}(x) \right|}$

Ist die Funktion f zusätzlich noch reellwertig in [a,b], dann kann man mit Hilfe des Mittelwertsatzes der Integralrechnung folgende Darstellung für das Restglied herleiten:

$E(f) = {(b-a)^{m+2} \over (m+1)!}{\beta_{m+1}}{f^{(m+1)}(\zeta)}$

mit einer Zwischenstelle ζ im Intervall [a,b].

Weitere Quadraturformeln

Der Versuch, die Fehlerordnung der Quadraturformel zu minimieren, führt auf die Gauß-Quadratur. Diese nutzen die Theorie orthogonaler Polynome, um Formeln zu erhalten, die Polynome vom Grad 2m exakt integrieren, wobei m die Anzahl der genutzten Funktionsauswertungen ist.

Um die Anzahl der Funktionsauswertungen zu minimieren, bei gleichzeitiger Möglichkeit den Fehler zu kontrollieren, verwendet man oft das Rombergsche Extrapolationsverfahren. Hierbei werden die Integralwerte von immer kleiner werdenden 'Streifen' zu einer verschwindenden Breite hin extrapoliert.

Summierte Quadraturformeln

Um das Integral noch besser annähern zu können unterteilt man das Intervall [a,b] in N nebeneinanderliegende Teilintervalle. Die Teilintervalle müssen nicht die gleiche Länge haben. In jedem Teilintervall wendet man im Folgenden die gleiche Näherung für die einzelnen Flächen an und addiert danach die entstandenen Näherungen. Von besonderem Interesse sind adaptive Formeln, die in Abhängigkeit von einer Fehlerschätzung einzelne Teilintervalle unterteilen, solche in denen der Fehler bereits unter einer Schranke ist, aber nicht.

Literatur

• Hans R. Schwarz, Norbert Köckler: Numerische Mathematik. 6. Auflage, Teubner, Stuttgart 2006, ISBN 3-519-42960-8