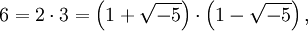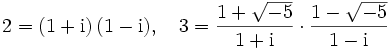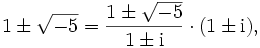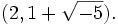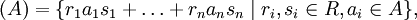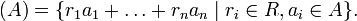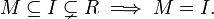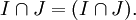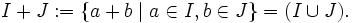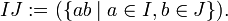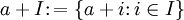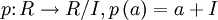Zweiseitiges Ideal

In der abstrakten Algebra ist ein Ideal eines Ringes R eine Teilmenge I, die abgeschlossen bezüglich R-Linearkombinationen ist.

Die Bezeichnung „Ideal“ ist abgeleitet aus dem Begriff „ideale Zahl“: Ideale können als Verallgemeinerung von Zahlen angesehen werden.

„Ideale Zahlen“

Der Ursprung der Ideale liegt in der Feststellung, dass in Ringen wie $\mathbb Z[\sqrt{-5}]$ die Eindeutigkeit der Zerlegung in irreduzible Elemente nicht gilt: So ist

$6 = 2\cdot 3 = \left(1+\sqrt{-5}\right)\cdot\left(1-\sqrt{-5}\right),$

und die beiden Faktoren jeder Zerlegung sind irreduzibel. Ernst Kummer stellte fest, dass man die Eindeutigkeit manchmal wiederherstellen kann, indem man weitere, ideale Zahlen hinzunimmt. Im Beispiel erhält man durch Hinzunahme der Zahl i die Faktorisierungen

$2=\left(1+\mathrm i\right)(1-\mathrm i),\quad 3=\frac{1+\sqrt{-5}}{1+\mathrm i}\cdot\frac{1-\sqrt{-5}}{1-\mathrm i}$

(dass die Brüche auf der rechten Seite ganz sind, kann man an ihren Normen sehen) sowie

$1\pm\sqrt{-5}=\frac{1\pm\sqrt{-5}}{1\pm\mathrm i}\cdot(1\pm\mathrm i),$

und die Eindeutigkeit ist wiederhergestellt.^[1] Aus heutiger Sicht entspricht die Einführung der idealen Zahl i dem Übergang zum hilbertschen Klassenkörper, in dem alle Ideale des kleineren Körpers zu Hauptidealen werden.

Richard Dedekind erkannte, dass man diese idealen Zahlen vermeiden kann, indem man statt ihrer die Gesamtheit aller durch sie teilbaren Zahlen betrachtet. So haben die Zahlen 2 und 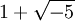$1+\sqrt{-5}$ im Beispiel den gemeinsamen idealen Primfaktor 1 + i, und die in $\mathbb Z[\sqrt{-5}]$ liegenden Vielfachen dieser Zahl sind gerade das Primideal

$(2,1+\sqrt{-5}).$

Ist ein „realer“ gemeinsamer Faktor vorhanden, so besteht das Ideal gerade aus seinen Vielfachen, ist also ein Hauptideal.^[2] In Ganzheitsringen von Zahlkörpern (und allgemeiner in der aufgrund dieser Tatsache nach ihm benannten Klasse der Dedekindringe) erhält man auf diese Weise eine eindeutige Zerlegung jedes Ideals (ungleich null) in Primideale.^[3]

Definition

Um auch für nichtkommutative Ringe geeignete Begriffe zu haben, unterscheidet man zwischen Links-, Rechtsidealen und zweiseitigen Idealen:

Es sei I eine Teilmenge eines Ringes R. I heißt dann Linksideal, wenn gilt:

1: Die Null des Ringes liegt in I.

2: Für alle a,b in I liegt a − b in I.

3L: Für jedes a in I und r in R liegt ra in I.

Entsprechend ist I ein Rechtsideal, wenn für I neben 1 und 2 auch gilt:

3R: Für jedes a in I und r in R liegt ar in I.

I nennt man schließlich zweiseitiges Ideal oder nur kurz Ideal, falls I Links- und Rechtsideal ist, also 1, 2, 3L und 3R erfüllt.

Bemerkungen

• Da ein Ideal I die 0 enthält, ist es nicht leer. Tatsächlich genügt an Stelle von Bedingung 1 schon die Forderung, dass I nicht leer ist.
• Die Forderungen 1 und 2 sind äquivalent zu der Aussage, dass (I, + ) eine Untergruppe der additiven Gruppe (R, + ) ist.
• Ein Links- ebenso wie ein Rechtsideal in R ist nichts anderes als ein Untermodul von R, aufgefasst als R-Links- bzw. R-Rechtsmodul.
• Ist der Ring kommutativ, dann fallen alle drei Begriffe zusammen, in einem nichtkommutativen Ring können sie sich aber unterscheiden.

Beispiele

• Die Menge 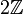$2\mathbb{Z}$ der geraden ganzen Zahlen ist ein Ideal im Ring $\mathbb{Z}$ aller ganzen Zahlen.
• Die Menge 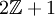$2\mathbb{Z}+1$ der ungeraden ganzen Zahlen ist kein Ideal in $\mathbb{Z}$; sie erfüllt keine der drei Bedingungen.
• Die Menge aller Polynome mit reellen Koeffizienten, die durch x² + 1 teilbar sind, bilden ein Ideal im Polynomring $\mathbb{R}[X]$. (Der Körper $\mathbb{R}[X]/(x^2+1)$ ist isomorph zu den komplexen Zahlen)
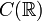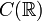• Der Ring $C(\mathbb{R})$ aller stetigen Funktionen von $\mathbb{R}$ nach $\mathbb{R}$ enthält das Ideal der Funktionen f mit f(1) = 0. Ein anderes Ideal in $C(\mathbb{R})$ sind die stetigen Funktionen mit kompaktem Träger, d. h. alle Funktionen, die für hinreichend große Argumente gleich 0 sind.
• Die Mengen {0} und R sind stets Ideale eines Rings R. Wenn {0} und R seine einzigen zweiseitigen Ideale sind, nennt man R einfach. Ein kommutativer einfacher Ring ist ein Körper.

Besondere Ideale

Alle Links-, alle Rechtsideale und alle zweiseitigen Ideale bilden jeweils ein Hüllensystem, die zugehörigen Idealoperatoren werden mit 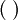$(\;)$, selten auch mit 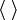$\langle\;\rangle$ bezeichnet.

Ist A eine Teilmenge des Ringes R, dann nennt man

$(A) := \bigcap_{J\ \mathrm{Ideal\ von}\ R,\ A \subseteq J} J$

das von A erzeugte Ideal, es ist das kleinste (Links-, Rechts- bzw. zweiseitige) Ideal in R, das A enthält.

Besitzt R ein Einselement 1, so ist

$(A) = \{r_1a_1s_1+\ldots+r_na_ns_n\mid r_i,s_i\in R, a_i\in A\},$

und wenn R zusätzlich noch kommutativ ist, gilt sogar:

$(A) = \{r_1a_1+\ldots+r_na_n\mid r_i\in R, a_i\in A\}.$

Das von einem Element a erzeugte Hauptideal ist

$(a) := \left(\{a\}\right)$.

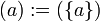Ein Ideal I heißt echt, wenn es nicht ganz R ist. Dies ist bei Ringen mit 1 genau dann der Fall, wenn 1 nicht in I liegt.

Ein echtes Ideal M heißt maximal, wenn es kein größeres echtes Ideal gibt, d. h. wenn für jedes Ideal I gilt

$M \subseteq I \subsetneq R \implies M = I.$

Mit Hilfe des Lemma von Zorn kann gezeigt werden, dass jedes echte Ideal eines Rings mit 1 in einem maximalen Ideal enthalten ist. Insbesondere besitzt jeder Ring mit 1 (außer der Nullring) ein maximales Ideal.

Ein echtes Ideal P heißt prim, wenn für alle Ideale I, J gilt:

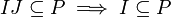$IJ \subseteq P \implies I \subseteq P$ oder $J \subseteq P.$

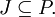
Jedes maximale Ideal in einem Ring mit 1 ist prim.

Verknüpfungen von Idealen

Für zwei Ideale 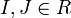$I, J \in R$ gilt:

• Der (mengentheoretische) Durchschnitt ist ein Ideal:

$I\cap J = (I\cap J).$

• Die mengentheoretische Vereinigung 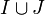$I\cup J$ ist im allgemeinen kein Ideal.
• Die Summe ist jedoch ein Ideal:

$I+J := \{a+b\mid a\in I,b\in J\} = (I\cup J).$

Wichtig: Summen und Vereinigungen von Idealen sind im Allgemeinen unterschiedliche Konstrukte!

• Als Produkt von I und J wird das Ideal definiert, das von der Menge der Produkte von Elementen aus I mit Elementen aus J (auch Komplexprodukt genannt) erzeugt wird:

$IJ := (\{ ab\mid a\in I,b\in J\}).$

Bemerkungen

• Das Komplexprodukt selbst ist im Allgemeinen kein Ideal.
• Das Produkt zweier Ideale ist stets in ihrem Schnitt enthalten.
• Mit den Verknüpfungen Summe und Durchschnitt bildet die Menge aller Ideale eines Ringes einen modularen, algebraischen Verband.
• Einige wichtige Eigenschaften dieser Verknüpfungen werden in den Noetherschen Isomorphiesätzen zusammengefasst.

Faktorringe und Kerne

Ideale sind wichtig, weil sie als Kerne von Ringhomomorphismen auftreten und die Definition von Faktorringen ermöglichen.

Ein Ringhomomorphismus f vom Ring R in den Ring S ist eine Funktion mit

$\begin{array}{lll} f(a+b) = f(a) + f(b), &f(ab) = f(a)f(b), &f(1) = 1 \end{array}$.

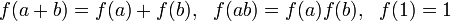Der Kern von f ist definiert als

$\ker \left(f\right) \colon = \left\{a \in R \colon f \left(a\right) = 0\right\}$.

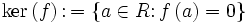Der Kern ist stets ein zweiseitiges Ideal von R.

Startet man umgekehrt mit einem zweiseitigen Ideal I von R, dann kann man den Faktorring R/I (sprich: „R modulo I“; Achtung: der Begriff ``Faktorring´´ ist ein anderer als der eines ``faktoriellen Rings´´!) definieren, dessen Elemente die Form

$a+I\colon =\left\{a+i\colon i \in I\right\}$

für ein a aus R haben. Die Abbildung

$p\colon R\to R/I, p\left(a\right) = a + I$

ist ein surjektiver Ringhomomorphismus, dessen Kern genau das Ideal I ist. Damit sind die Ideale eines Rings R genau die Kerne von Ringhomomorphismen von R.

Ist der Ring R kommutativ und I ein Primideal, dann ist R/I ein Integritätsring, ist I ein maximales Ideal, dann ist R/I sogar ein Körper.

Die extremen Beispiele von Faktorringen eines Ringes R entstehen durch Herausteilen der Ideale {0} oder R. Der Faktorring R/{0} ist isomorph zu R, und R/R ist der triviale Ring {0}.

Norm eines Ideals

Für Ganzheitsringe A eines Zahlkörpers K lässt sich eine Norm eines (ganzen) Ideals 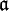$\mathfrak{a}$ definieren durch 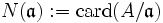$N(\mathfrak{a}) := \mathrm{card}(A / \mathfrak{a})$. Diese Norm ist immer eine endliche Zahl und steht in Zusammenhang mit der Norm der Körperweiterung 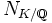$N_{K/\mathbb{Q}}$, nämlich gilt für Hauptideale Aa: 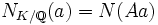$N_{K/\mathbb{Q}}(a) = N(Aa)$. Zudem ist diese Norm multiplikativ, d. h. 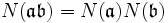$N(\mathfrak{a}\mathfrak{b}) = N(\mathfrak{a}) N(\mathfrak{b})$. Allgemeiner werden diese Normen auch für Ideale in Ordnungen in Zahlkörpern betrachtet.

Literatur

• Felix Klein, Vorlesungen über die Entwicklung der Mathematik im 19. Jahrhundert, Teil I. Berlin 1926
• Ernst Kummer, Über die Zerlegung der aus Wurzeln der Einheit gebildeten complexen Zahlen in ihre Primfactoren, J. reine angew. Math. 35 (1847) 327–367

Einzelnachweise

1. ↑ Klein, a.a.O., Kapitel VII, Abschnitt Theorie der algebraischen ganzen Zahlen …, S. 321f.
2. ↑ Klein, a.a.O., S. 323
3. ↑ J. Neukirch, Algebraische Zahlentheorie. Springer-Verlag, Berlin 1992. ISBN 3-540-54273-6; Theorem I.3.3