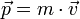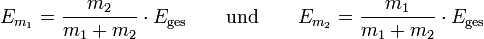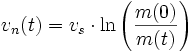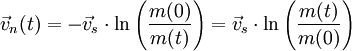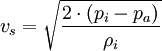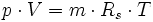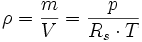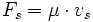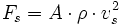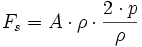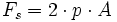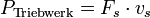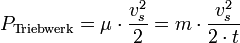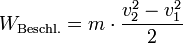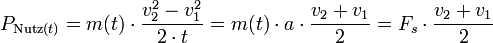Reaktionsantrieb

Rückstoßprinzip einer Rakete

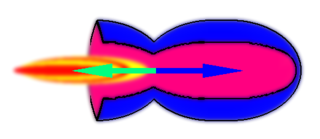
Der Rückstoßantrieb oder Reaktionsantrieb ist eine praktische Anwendung des 3. Newtonschen Axioms. Das angetriebene Objekt, zum Beispiel eine Rakete, wird durch den Rückstoß mit der gleichen Kraft nach vorn beschleunigt, mit der das Antriebsmedium nach hinten ausgestoßen wird.

Physikalischer Hintergrund

Entsprechend dem 3. Newtonschen Axiom (actio = reactio) werden zwei Massen, die eine Kraft aufeinander ausüben, beschleunigt. Somit ergibt sich für beide Massen (nach Beendigung der Krafteinwirkung) eine Geschwindigkeit. Entsprechend der Definition für den Impuls

$\vec p = m \cdot \vec v$

ergeben sich für diesen Fall folgende Relationen der Impulse zueinander:

$\vec{p}_1 = -\vec{p}_2 \qquad \mathrm{oder} \qquad m_1 \cdot \vec v_1 = m_2 \cdot -\vec v_2$

Dabei ist zu berücksichtigen, dass zur Erzeugung dieser Impulse eine definierte Energie zur Verfügung stehen muss, welche die entsprechende Beschleunigungsarbeit verrichten kann. Hat eine Masse einen Impuls, verfügt sie über eine kinetische Energie.

Bei der Berechnung der anteiligen Energiemengen gilt:

$E_{m_1} = \frac{m_2}{m_1 + m_2} \cdot E_\mathrm{ges} \qquad \mathrm{und} \qquad E_{m_2} = \frac{m_1}{m_1 + m_2}\cdot E_\mathrm{ges}$

Bei einem kontinuierlichen Prozess ergibt sich folgender, auch als Raketengrundgleichung bekannter, mathematischer Zusammenhang:

$v_n(t) = v_s \cdot \ln\left(\frac{m(0)}{m(t)}\right)$

oder auch:

$\vec{v}_n(t) = -\vec{v}_s \cdot \ln \left(\frac{m(0)}{m(t)}\right)= \vec{v}_s \cdot \ln \left(\frac{m(t)}{m(0)}\right)$

Wobei v_s gleich der Relativgeschwindigkeit der Stützmasse zur eigentlichen Nutzmasse ist. Hierbei ist zu berücksichtigen, dass bei Fortschreiten des Prozesses die Stützmasse kontinuierlich abnimmt und schlussendlich nur noch die Nutzmasse mit ihrer Endgeschwindigkeit v_n (relativ zum Startort) verbleibt.

Ein erstaunlicher Effekt stellt sich bei einem Verhältnis von 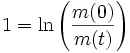$1 = \ln\left(\frac{m(0)}{m(t)}\right)$ ein. Ab diesem Zeitpunkt bewegt sich die Rakete sowie die von ihr ausgeworfenen Stützmasse von einem am Startort der Rakete verbliebenen Beobachter in die gleiche Richtung weg, allerdings mit unterschiedlichen Geschwindigkeiten.

Nachfolgend einige Erläuterungen zu Rückstoßantrieben, die auf der Basis von Fluiden arbeiten.

Ausströmgeschwindigkeit

In der Rückstoßkammer ist der Druck (p_i) höher als der Umgebungsdruck (p_a). Das in der Kammer befindliche Medium tritt auf Grund dieser Druckdifferenz mit einer bestimmten Geschwindigkeit (v_s) aus der Düse aus. Von Bedeutung ist weiterhin die Dichte (ρ) des ausströmenden Mediums.

$v_s = \sqrt {\frac {2 \cdot (p_i - p_a)}{\rho_i}}$

Bei Gasen ist zu beachten, dass deren Dichte (ρ) abhängig vom Druck und der Temperatur ist. Diese lässt sich (näherungsweise) mittels der Thermischen Zustandsgleichung idealer Gase

$p \cdot V = m \cdot R_s \cdot T$

durch Umstellung nach

$\rho = \frac {m}{V} = \frac {p}{ R_s \cdot T}$

berechnen.

Da bei Gasen die Dichte proportional zum Druck ist, kann eine Erhöhung der Austrittsgeschwindigkeit nur durch eine Temperaturerhöhung erzielt werden.

Durchsatz

Entsprechend dem Querschnitt (A) der Düse, der Dichte (ρ) des austretenden Mediums und dessen Austrittsgeschwindigkeit (v_s) lässt sich der oft auch als Massenstrom bezeichnete Durchsatz (μ) ermitteln.

$\mu = A \cdot \rho \cdot v_s$

Schub

Die erzeugte Schubkraft (F_s) kann durch die Multiplikation des Durchsatzes (μ) mit der Austrittsgeschwindigkeit (v_s) des Mediums berechnet werden.

$F_s = \mu \cdot v_s$

Oder durch Ersetzen von $\mu = A \cdot \rho \cdot v_s$

$F_s = A \cdot \rho \cdot v_s^2$

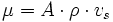
und

$F_s = A \cdot \rho \cdot \frac {2 \cdot p}{\rho}$

erhält man die massenunabhängige Beziehung

$F_s = 2 \cdot p \cdot A$

Benötigte Triebwerksleistung

Hierbei ist nicht die Leistung (P_Nutz) gemeint, mit der ein solches Triebwerk eine Masse bewegen (beschleunigen) würde, sondern die Leistung, die benötigt wird, um die entsprechende Schubkraft zu erzeugen.

$P_\mathrm{Triebwerk} = F_s \cdot v_s$

Oder man ermittelt diese Leistung (P_Triebwerk) über den gegebenen Durchsatz (μ).

$P_\mathrm{Triebwerk} = \mu \cdot \frac {v_s^2}{2} = m \cdot \frac {v_s^2}{2 \cdot t}$

Um bei einem hypothetischem Photonenantrieb die gleiche Schubkraft zu erzeugen, müsste die Triebwerksleistung erheblich höher liegen als bei einem herkömmlichen chemischen Raketenantrieb.

Nutzleistung

Die tatsächliche von einem solchen Rückstoßantrieb umsetzbare Leistung (P_Nutz(t)) ergibt sich durch Umstellung der Formel für die Beschleunigungsarbeit:

$W_\mathrm{Beschl.} = m \cdot \frac {v_2^2-v_1^2}{2}$

$P_{\mathrm{Nutz}(t)} = m(t) \cdot \frac {v_2^2-v_1^2}{2 \cdot t} = m(t) \cdot a \cdot \frac {v_2 + v_1}{2} = F_s \cdot \frac {v_2 + v_1}{2}$

Dabei stellen v₁ die Anfangsgeschwindigkeit und v₂ die Endgeschwindigkeit des Beschleunigungsvorganges dar.

Rückstoßantrieb in der Natur

Quallen und Tintenfische, wie Kalmare und Sepien, können sich fortbewegen, indem sie Wasser in einen körpereigenen Hohlraum einströmen lassen und anschließend durch eine Kontraktion des umgebenden Gewebes entgegen ihrer Bewegungsrichtung ausstoßen. Insbesondere Kalmare können dabei durch die Bündelung des Wasserstrahls mittels eines Siphos relativ hohe Geschwindigkeiten erreichen.^[1] Hierbei wird das Wasser mit niedriger Geschwindigkeit angesaugt, so dass der Impulsunterschied durch Reibung an das umgebende Meer weitergegeben werden kann, der Ausstoß erfolgt bei hoher Geschwindigkeit und Stromlinienform des Körpers, so dass ein großer Teil des Impulses zur Fortbewegung genutzt werden kann.

Auch junge Anglerfische nutzen den Rückstoßantrieb, indem sie Wasser in ihr Maul saugen, das sein Volumen dabei versechsfachen kann, und es danach durch die weit hinten liegenden Kiemenöffnungen pressen. Dadurch können kurzzeitig deutlich höhere Geschwindigkeiten erreicht werden als durch Schwimmen.

Anwendungen

• Aeolipile - Durch Heron von Alexandria erfundene, dampfgetriebene Turbine
• Wasserstrahlantrieb
• Raketentriebwerk
• Strahltriebwerk
• Staustrahltriebwerk
• Verpuffungsstrahltriebwerk
• Ionenantrieb
• Magnetohydrodynamischer Antrieb
• Magnetoplasmadynamischer Antrieb

Siehe auch

Bernoulli-Gleichung

Weblinks

• Impulssatz und Energiesatz
• Der Begriff der Arbeit (Beschleunigungsarbeit)
• Eine andere Methode der Beschleunigung
• Neue Antriebstechnologien

Belege

1. ↑ Arche Online: Kalmar