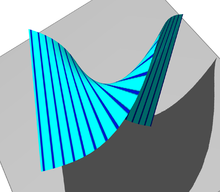
- Regelfläche
-
Eine Regelfläche ist in der Mathematik eine (zweidimensionale) Fläche, die auf bestimmte Weise aus Geraden zusammengesetzt ist. Der Begriff „Regelfläche“ entstand aus einer Falschübersetzung des englischen Begriffs „ruled surface“: So bedeutet „rule“ nicht nur „Regel“, sondern auch „linieren“.
Im dreidimensionalen anschaulichen euklidischen Vektorraum sind abwickelbare Flächen auch stets Regelflächen, sonst gilt dies nicht.
Definition
Eine zweidimensionale differenzierbare Mannigfaltigkeit heißt Regelfläche, wenn sie die Vereinigung einer einparametrigen Geradenschar ist. Die Geraden dieser Schar heißen die Erzeugenden der Regelfläche. Die Tangentialebenen in den Punkten einer Erzeugenden e enthalten stets diese Erzeugende, und für sie gilt genau eine der beiden Aussagen (aber nicht beide Aussagen zugleich):
- Die Tangentialebenen in allen Punkten von e sind identisch. Diese Erzeugende heißt dann Torsale.
- Durchläuft ein (Berühr-)Punkt B die Erzeugende e, so dreht sich die zugehörige Tangentialebene um e, und alle Ebenen, die die Gerade e enthalten, kommen bis auf eine Ausnahmeebene alle als Tangentialebene der Regelfläche in einem Punkt von e vor.
Jede Erzeugende einer Regelfläche ist eine Asymptotenlinie der Regelfläche.
Beispiele
- Die Ebene
- Mantelfläche des Zylinders und Kegels
- Die Einhüllende einer einparametrigen Ebenenschar
- Vereinigung der Tangenten einer Raumkurve; die zugehörige Raumkurve ist die Gratlinie oder Rückkehrkante; sie ähnelt einer Messerschneide.
- Hyperbolisches Paraboloid
- Einschaliges Hyperboloid (In der Landschaft manchmal zu sehen als Kühlturm eines Kraftwerks)
- Oloid
Sind alle Erzeugenden torsal, so wird die Regelfläche Torse genannt. Die Gesamtheit der Torsen besteht aus Tangentenflächen, Kegeln, Zylindern und Ebenen, d. h. jede Torse ist nach geeigneter Zerlegung aus diesen Flächenstücken zusammengesetzt. Sie sind die einzigen Flächen, die in eine Ebene abgewickelt werden können.
Die ersten Beispiele haben die Gaußsche Krümmung 0 und sind daher in die Ebene abwickelbar. Hyperbolisches Paraboloid und Drehhyperboloid haben überall negative Gaußsche Krümmung und werden windschiefe Regelflächen genannt. Es sind die beiden einfachsten windschiefen Regelflächen.
Eigenschaften
Man kann je zwei abwickelbare Regelflächen längs einer Geraden g bzw. h abschneiden und sie so zusammensetzen, dass aus g und h eine gemeinsame Gerade der zusammengesetzten Fläche mit einer neuen gemeinsamen Tangentialebene von dieser wird.
Bei einer nicht abwickelbaren und einer abwickelbaren Regelfläche ist die so zusammengesetzte Fläche längs der gemeinsamen Erzeugenden nicht differenzierbar. Die gemeinsame Erzeugende ist als Kante sichtbar, wobei die Kante an verschiedenen Punkten der Erzeugenden verschieden deutlich hervortritt. Bei zwei nicht abwickelbaren Regelflächen kann die so zusammengesetzte Fläche längs der gemeinsamen Erzeugenden differenzierbar sein, ist es im allgemeinen aber nicht.
Kategorie:- Elementare Differentialgeometrie
Wikimedia Foundation.