Oloid

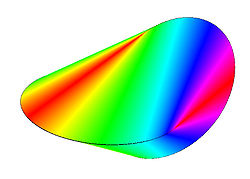
Das Oloid ist ein geometrischer Körper, der 1929 vom Bildhauer und Maschinenbauer Paul Schatz entdeckt wurde. Es kann definiert werden als die konvexe Hülle zweier gleichgroßer Kreise, die bis an die Mittelpunkte senkrecht ineinander geschoben sind. Der Abstand der Mittelpunkte ist dann gleich dem Radius der Kreise. Das Oloid hat keine Ecken und nur die beiden äußeren Kreisbögen als Kanten (jeweils 240°), ansonsten ist es glatt. Es besitzt mehrere Eigenschaften, die es deutlich von anderen geometrischen Körpern unterscheiden und die es mathematisch zu einem interessanten Objekt machen. Schatz hat es zusammen mit dem umstülpbaren Würfel erfunden. Es gilt auch als Plausibilitätshinweis für die von Schatz begründete Inversionskinematik.

Oloid

Kontext

Das Oloid als Regelfläche, die eine Diagonale der Würfelkette von Schatz überstreicht: Die Enden der Diagonale (weiße Linie) bewegen sich auf zwei gekreuzten Kreisbögen (blau und rot) hin und her.

Paul Schatz entdeckte in den 1920er Jahren eine Zerlegung des Würfels in drei Teile, bei der ein Teil aus einer Kette aus unregelmäßigen Tetraedern besteht, die sich komplett umstülpen lässt.

Oloid: Konturlinien zwischen den beiden Bestimmungskreisen

Die Tetraeder sind an je zwei gegenüber liegenden zueinander rechtwinkligen Kanten gelenkig miteinander verbunden. Die ausgebreitete Kette hat zwischen gegenüberliegenden Gelenken drei gleich lange Diagonalen. Es handelt sich um Raum-Diagonalen des ursprünglichen Würfels, die auch während des Umstülpens erhalten bleiben (konstante Länge). Schatz beobachtete den Weg, den eine solche Diagonale beim Umstülpen der Kette nimmt und entdeckte dabei das Oloid. Fixiert man einen der Tetraeder und beobachtet den Weg der ihm gegenüber liegende Diagonalen, so erkennt man, dass die von ihr überstrichene Fläche die Oberfläche (Regelfläche) eines geometrischen Körpers ist, den Schatz Oloid nannte.

1997 beschrieben Hellmuth Stachel und Hans Dirnböck in ihrer Arbeit The Development of the Oloid die mathematischen Eigenschaften aus analytischer Sicht.^[1]

Das Oloid ist Teil des Oloid-Rührers, der zum Umwälzen und Belüften von Wasser, z. B. in der Abwasserreinigung und Gewässersanierung, eingesetzt wird.^[2] Eine weitere Anwendungsform als Alternative zum Schiffspropeller hat bislang nicht das Stadium von Prototypen und Versuchen überschreiten können.

abgewickeltes Oloid

Eigenschaften

Das Oloid ist der einzige bekannte Körper, der über seine gesamte Oberfläche abrollt: Setzt man es auf eine Schräge, so rollt es in einer taumelnden Bewegung aber einer geraden Bahn hinunter, ohne dabei jemals über seine Kanten zu poltern. Ähnlich wie die Mantelfläche eines Kegels oder Zylinders lässt sich das Oloid knickfrei aus einem Stück Pappe herstellen, nur dass man hier tatsächlich die gesamte Oberfläche erhält. (Siehe auch abwickelbare Fläche). Bemerkenswert ist, dass die Größe der Oberfläche gleich ist wie die einer Kugel, die den gleichen Radius hat wie die beiden das Oloid erzeugenden Kreise.

Der Winkel an den Kanten beträgt 60°. Betrachtet man das Oloid senkrecht zu den beiden Kanten, so bilden die Konturen im Querschnitt exakt ein Quadrat, was bei handwerklich hergestellten Oloiden eine Qualitätseinschätzung möglich macht, da leichte Unsymmetrien schnell erkannt werden.

Mathematik

Das Oloid als Teil einer algebraische Fläche achten Grades

rausgezoomt...

Im Weiteren sei R der Radius der erzeugenden Kreise. Die beiden Kanten haben jeweils eine Länge von $\frac{4}{3} \pi R$. Die Oberfläche ist eine Regelfläche, zu jedem Punkt x gibt es (bis auf Spiegelung) genau einen Punkt y auf der anderen Kante, sodass das die Verbindungsstrecke komplett auf der Oberfläche des Oloids liegt. Die Länge der Strecke ist für alle Punkte dieselbe, nämlich $\sqrt{3} R$.

Parametrisierung

...noch weiter rausgezoomt

Für eine Einbettung in den dreidimensionalen euklidischen Raum setze den Mittelpunkt des liegenden Kreises auf den Ursprung, den des stehenden Kreises auf (0,R,0). Damit ist für $t \in \left[\frac{\pi}{3},\frac{5\pi}{3}\right]$ der Punkt x = (x₁,x₂,0) auf dem liegenden Kreis gegeben durch x₁ = Rcos(t) und x₂ = Rsin(t). Den korrespondierenden Punkt y = (y₁,0,y₃) auf dem stehenden Kreis erhält man mittels $y_1=\frac{R}{1-\cos(t)}$ und $y_3= \pm \frac{R \sqrt{1-2\cos(t)}}{1-\cos(t)}$. Je nach Vorzeichen ist dies ein Punkt auf der oberen oder unteren Hälfte des Oloids.

Mit Hilfe der Geradengleichung gelangt man nun zu folgender Parametrisierung der Oberfläche: $\Phi: [0,1] \times\left[\frac{\pi}{3},\frac{5\pi}{3}\right] \to \mathbb R^3;$ Φ(s,t) = (Φ₁,Φ₂,Φ₃) mit

$\Phi_1= R \left (\frac{s}{1-\cos(t)}+(1-s)\cos(t)\right )$

Φ₂ = (1 − s)Rsin(t)

$\Phi_3= \pm \frac{sR\sqrt{1-2\cos(t)}}{1-\cos(t)}$

Für theoretische Betrachtungen ist eine Einschränkung des Parameterbereichs von t auf $\left[\frac{\pi}{2},\frac{3\pi}{2}\right]$ (also auf ein Achtel der Oberfläche) möglich, aufgrund der Symmetrie. Auch zur Visualisierung kann dies sinnvoll sein. Eine Koordinatendarstellung ist noch nicht bekannt.

Oberfläche und Volumen

Mit Hilfe des Kreuzproduktes und der partiellen Ableitungen der Parametrisierung lässt sich das Oberflächenintegral berechnen. Es stellt sich heraus, dass die Oberfläche gerade eine Größe von 4πR² hat - ebenso wie eine Kugel vom Radius R. Eine Formel für das Volumen ist durch das Integral

$8R^3 \int_{-1}^{1} \frac{dx}{(3+x)\sqrt{(1-x^2)(9-x^2)}} = \frac{R^3}{3} \left( \Pi(3/4,\sqrt{3}/2) + 2K(\sqrt{3}/2) \right)$

gegeben, wo Π,K vollständige elliptische Integrale bezeichnet. Numerische Berechnungen ergaben ca. 3,05R³.^[3]

Die Oloid-Fläche

Das Oloid kann als Teil der algebraischen Fläche vom Grad 8 (also eine Oktik) gesehen werden. Die definierende Polynomgleichung O besteht aus 48 Termen, das Maximum der Exponentensummen der Monome ist 8 und es gibt keinen konstanten Term. Durch (x − 0,5) wird die Fläche auf der x-Achse so verschoben, dass der Mittelpunkt im Nullpunkt liegt.

O:(x − 0,5)⁸ − 3y⁸ − 3z⁸ − 6(x − 0,5)⁴y⁴

− 8(x − 0,5)²y⁶ − 6(x − 0,5)⁴z⁴ − 8(x − 0,5)²z⁶ + 6y²z⁶

+ 12(x − 0,5)²y²z⁴ − 9y⁴z⁴ + 6y⁶z² + 12(x − 0,5)²y⁴z²

+ 6(x − 0,5)⁴y²z² + 4(x − 0,5)⁷ + 12(x − 0,5)³y⁴ + 4(x − 0,5)y⁶

− 20(x − 0,5)z⁶ − 36(x − 0,5)³z⁴ + 12(x − 0,5)³y²z² + 24(x − 0,5)y⁴z²

− 12(x − 0,5)⁵z² + 12(x − 0,5)⁵y² + 2(x − 0,5)⁶ + 10y⁶

− 2z⁶ + 22(x − 0,5)²y⁴ − 46(x − 0,5)²y²z² − 50(x − 0,5)²z⁴

− 12y²z⁴ − 46(x − 0,5)⁴z² + 14(x − 0,5)⁴y² − 8(x − 0,5)⁵

− 8(x − 0,5)y⁴ − 8(x − 0,5)z⁴ − 52(x − 0,5)y²z² − 48(x − 0,5)³z²

− 16(x − 0,5)³y² − 7(x − 0,5)⁴ − 11y⁴ + z⁴

− 18(x − 0,5)²y² − 6(x − 0,5)²z² − 10y²z² + 4(x − 0,5)³

+ 4(x − 0,5)y² + 4(x − 0,5)z² + 4(x − 0,5)² + 4y² = 0

Einzelnachweise

1. ↑ http://www.heldermann-verlag.de/jgg/jgg01_05/jgg0113.pdf
2. ↑ Oloid-Rührer [1], unten
3. ↑ http://www.heldermann-verlag.de/jgg/jgg01_05/jgg0113.pdf (19. Mai 2008, pdf, Seite 13)

Literatur

• Paul Schatz: Rhythmusforschung und Technik 3. Auflage unter dem Titel: "Die Welt ist umstülpbar" im Verlag Niggli erhältlich.
• Spektrum der Wissenschaft: Mathematische Unterhaltungen III, Artikel: Eine Reise in das Reich des Würfels, Seiten 12 - 17, Dossier 2/2004

Weblinks

• Paul Schatz Stiftung
• Kuboid GmbH (u.a. mit einer brauchbaren Bastelmappe zum Oloid im Verkauf)
• Oloid AG («Rühren, Umwälzen, Belüften»)
• Das Oloid nach Paul Schatz
• Hans Dirnböck, Hellmuth Stachel: The Development of the Oloid
• weitere Details und Visualisierungen

 Commons: Oloid surface – Sammlung von Bildern, Videos und Audiodateien