Automatenmodell

Ein Automat oder eine abstrakte Maschine ist in der Informatik das Modell eines digitalen, zeitdiskreten Rechners. Ob es möglich oder sinnvoll ist, eine solche Maschine tatsächlich zu bauen, ist dabei zunächst unerheblich. Die Vereinfachung der Fähigkeiten erlaubt es, das Verhalten eines Automaten leichter zu verstehen und zu vergleichen – darauf kommt es an.

Der Automatenbegriff spielt eine zentrale Rolle in der Theoretischen Informatik. In der Berechenbarkeitstheorie und in der Komplexitätstheorie etwa stellen die Automaten den zugrunde liegenden Berechnungsbegriff. Automaten spielen auch in der Praktischen Informatik eine entscheidende Rolle, zum Beispiel im Compilerbau. In der Digitaltechnik werden Automaten zur Steuerung in digitalen und hybriden Systemen eingesetzt. Solche Steuerungsautomaten haben Anwendungen unter anderem in der Rechnerarchitektur, in Rechnernetzen und in Reaktiven Systemen.

Verhalten eines Automaten

Das grundsätzliche Verhalten eines Automaten ist immer gleich: Dem Automaten wird von außen eine Eingabe als Folge von Zeichen vorgelegt. Der Automat hat einen Zustand. Jedes Mal, wenn ein Eingabezeichen eintrifft, kann sich abhängig vom Eingabezeichen und dem gegenwärtigen Zustand ein neuer Zustand, der Folgezustand, einstellen (Zustandsübergang oder Transition). Man kann die Menge der möglichen Zustandsübergänge, die das Verhalten des Automaten definiert, als das Programm des Automaten verstehen.

Deterministische und nichtdeterministische Automaten

Wenn der Folgezustand durch den gegenwärtigen Zustand und das Eingabezeichen immer eindeutig gegeben ist, dann spricht man von einem deterministischen Automaten. Allgemein aber kann man auch einen Spielraum (Freiheitsgrade) für die Zustandsübergänge zulassen. Der Automat darf dann auf dasselbe Paar von Zustand und Eingabezeichen unter mehreren möglichen Kandidaten einen Folgezustand willkürlich wählen. Dann spricht man von einem nichtdeterministischen Automaten. Der Nichtdeterminismus ist dann willkommen, wenn man das Verhalten der Umgebung modellieren möchte, das man nicht völlig genau kennt (don't know), oder wenn man Möglichkeiten für verschiedene Implementierungen offenlassen möchte (don't care).

Meist lässt man zusätzlich zu nichtdeterministischen Zustandsübergängen noch spontane Zustandsübergänge zu, das sind solche, die ohne Eingabezeichen stattfinden (ε-Übergänge).

Automaten mit und ohne Ausgabe

Automaten, die nur ihre Zustandsübergänge abwickeln, nennt man auch Transitionssysteme.

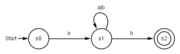
Daneben gibt es auch Automaten, die eine gewisse Teilmenge ihrer Zustände als Endzustände auszeichnen. Wenn ein Eingabewort den Automaten von einem ausgezeichneten Zustand, dem Startzustand, in einen der Endzustände führt, dann sagt man, der Automat akzeptiert das Eingabewort. Einen solchen Automaten nennt man deswegen einen Akzeptor. Ein Akzeptor eignet sich dazu, eine Formale Sprache zu definieren, nämlich die Menge aller endlichen Wörter, die der Automat akzeptiert.

Schließlich gibt es noch Automaten mit Ausgabe oder Transduktoren. Sie ordnen entweder jedem Zustand (Moore-Automaten) oder jedem Paar aus Zustand und Eingabezeichen (Mealy-Automaten) ein Ausgabezeichen zu. Auf diese Weise bildet ein Automat eine Verarbeitungseinheit.

Klassen von Automaten

Endlicher Automat

Registermaschine

Nach den Mitteln, die ein Automat zur Verfügung hat, kann man die Automaten in Klassen einteilen. Statt Klasse von Automaten sagt man auch Automatenmodell. Den Akzeptoren der jeweiligen Klasse kann man ihre akzeptierte Sprache zuordnen. Es stellt sich heraus, dass jeder Klasse von Automaten auf diese Weise eine Klasse Formaler Sprachen entspricht. Bekannte Klassen von Automaten sind (jeweils mit Abkürzungen für die deterministische und die nichtdeterministische Variante):

• Endliche Automaten (DFA/NFA): Ein endlicher Automat kennt nur endlich viele Zustände. Beide Klassen akzeptieren die Typ-3-Sprachen (Reguläre Sprachen)
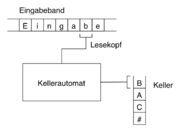
• Stapel, auf dem Zeichen zur späteren Verarbeitung zwischengespeichert werden können. Die PDAs akzeptieren die Typ-2-Sprachen (Kontextfreie Sprachen). Die DPDAs akzeptieren die deterministisch kontextfreien Sprachen.
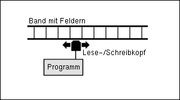
• Rekursiv aufzählbare Sprache). Durch die Turingmaschine wird außerdem der Begriff der Berechenbarkeit definiert. Siehe Churchsche These.
• Linear beschränkte Automaten (DLBA/LBA): Die linear beschränkten Automaten unterscheiden sich von den Turingmaschinen nur dadurch, dass der zugängliche Teil des Bandes durch die Größe der Eingabe beschränkt ist. Nichtdeterministische LBA akzeptieren genau die Typ-1-Sprachen (kontextsensitive Sprachen), die Frage ob das auch auf deterministische LBA zutrifft ist ein noch offenes Problem.
• Zweikellerautomat: Beim Zweikellerautomat hat man im Unterschied zum Kellerautomaten zwei Keller zur Verfügung. Durch das Kellerpaar kann ein Turingband simuliert werden. Die Zweikellerautomaten sind also den Turingmaschinen gleichwertig. Syntaktische Beschränkungen dieses Modells führen zur Charakterisierung der Typ-1- und Typ-2-Sprachen.
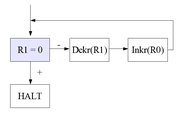
• Registermaschinen: Eine Registermaschine hat zusätzlich zum inneren Zustand eine Folge von Registern, das sind Speicherzellen für natürliche Zahlen, auf denen elementare Rechenoperationen ausgeführt werden können. Registermaschinen sind genau so mächtig wie Turingmaschinen.

Die Menge der Automaten stehen wie folgt mit den Mengen der Sprachklassen und Grammatiken in Beziehung (siehe auch Chomsky-Hierarchie):

Chomsky-Hierarchie	Sprachklasse		nicht deterministischer Automat		deterministischer Automat
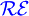
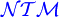
Typ-0-Grammatik	${\color{blue}\mathcal{RE}}$	=	${\color{blue}\mathcal{NTM}}$	=
Typ-1-Grammatik	${\color{blue}\mathcal{CS}}$	=	${\color{blue}\mathcal{LBA}}$	$\supseteq$	$\mathcal{DLBA}$
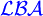
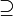
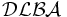
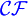
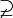
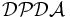
Typ-2-Grammatik	${\color{blue}\mathcal{CF}}$	=		$\varsupsetneq$	$\mathcal{DPDA}$
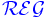
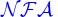
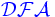
Typ-3-Grammatik	${\color{blue}\mathcal{REG}}$	=	${\color{blue}\mathcal{NFA}}$	=	${\color{blue}\mathcal{DFA}}$

Ob LBA ⊃ DLBA echt gilt, oder ob die DLBAs die gleiche Sprachklasse akzeptieren wie die LBAs, ist noch nicht bekannt.

Erweiterte Automatenbegriffe

Nichtdeterministische Automaten dürfen nicht verwechselt werden mit Stochastischen Automaten. Letztere ordnen den Zustandsübergängen Wahrscheinlichkeiten zu, während erstere nur über Möglichkeiten reden. Für Wahrscheinlichkeitsaussagen sind nichtdeterministische Automaten daher nicht geeignet.

Daneben gibt es weitere Automatentypen, die sich nicht am sequentiellen Einlesen einer Eingabe orientieren. Einige der bekannteren Automaten sind:

• Varianten der
• Zelluläre Automaten
• Neuronale Netze
• Petri-Netze

Anwendungen

Von praktischer Relevanz für die Programmierung sind vor allem Endliche Automaten und Kellerautomaten: sie bieten eine einfache Struktur, mit der sich viele komplexe Probleme übersichtlich lösen lassen. Im Compilerbau werden sie beispielsweise zur Implementierung von Parsern eingesetzt, die Umsetzungen von Netzwerkprotokollen benutzen häufig einen endlichen Automaten, um ihren aktuellen Zustand zu modellieren. Auch die Navigationsmöglichkeiten in einem Wizard lassen sich sehr gut als endlicher Automat ausdrücken, und das Workflow-Management benutzt diese Konzepte zur Modellierung von Arbeitsabläufen. Der Dateibaum eines Betriebssystems ist eigentlich kein Baum, sondern ein Endlicher Automat mit den inodes als Zuständen und den Dateinamen als Eingabezeichen.

Auch bei der Realisierung sequenzieller Hardware wird das Modell des Endlichen Automaten genutzt, dort meist als Finite State Machine (FSM) bezeichnet.

Siehe auch

• Automatentheorie
• Mathematische Maschine