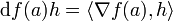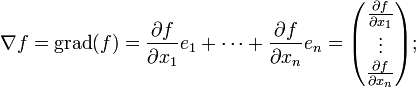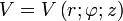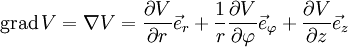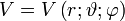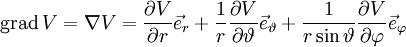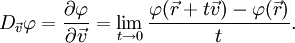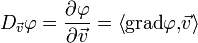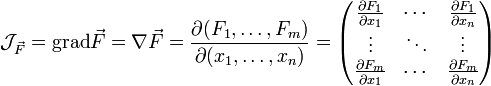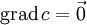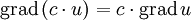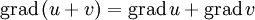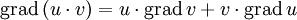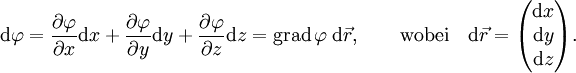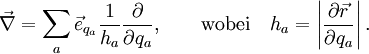Gradient eines Skalarfeldes

Zwei Skalarfelder dargestellt als Grauschattierung (dunklere Färbung entspricht größerem Funktionswert). Die blauen Pfeile darauf symbolisieren den zugehörigen Gradienten.

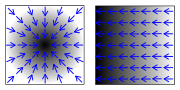
Der Gradient ist ein mathematischer Operator, genauer ein Differentialoperator, der auf ein Skalarfeld angewandt werden kann. Hierdurch erhält man ein Vektorfeld, das die Änderungsrate und die Richtung der größten Änderung des Skalarfeldes angibt.

Interpretiert man beispielsweise die Höhenkarte einer Landschaft als eine Funktion h(x,y), die jedem Ort die Höhe an dieser Stelle zuordnet, dann ist der Gradient von h an einer Stelle (x,y) ein Vektor, der in die Richtung des steilsten Anstieges zeigt, und dessen Länge ein Maß für die Steilheit (Steigung) ist.

Der Gradient zeigt dabei in die Richtung der Normalen der jeweiligen Linie, auf der die Werte des Skalarfeldes konstant sind (siehe auch Niveaumenge). Dabei ist der Gradient so orientiert, dass er in die Richtung wachsender Funktionswerte des Skalarfeldes zeigt. Der Betrag des Gradienten stimmt außerdem mit der Richtungsableitung der Funktion des Skalarfeldes in Normalenrichtung überein.

Der Gradient wird zusammen mit anderen Differentialoperatoren wie Divergenz und Rotation in der Vektoranalysis, einem Teilgebiet der mehrdimensionalen Analysis untersucht.

Gradient eines Skalarfeldes

Auf 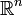$\R^{n}$ sei das Skalarprodukt 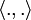$\langle.,.\rangle$ gegeben. Der Gradient der partiell differenzierbaren Funktion f im Punkt 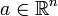$a \in \R^n$ ist der durch die Forderung

$\mathrm{d} f(a) h = \langle \nabla f(a) , h \rangle$

eindeutig bestimmte Vektor 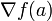$\nabla f(a)$. Der Operator d ist die totale Ableitung. Im Fall des Standardskalarproduktes ist 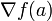$\nabla f(a)$ der Spaltenvektor

$\nabla f = \operatorname{grad}(f) = \frac{\partial f}{\partial x_1} e_1 + \cdots +\frac{\partial f}{\partial x_n} e_n = \begin{pmatrix} \frac{\partial f}{\partial x_1} \\ \vdots \\ \frac{\partial f}{\partial x_n} \end{pmatrix};$

gesprochen "Nabla-f(a)". Die Einträge 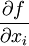$\frac{\partial f}{\partial x_i}$ sind die partiellen Ableitungen von f in x_i Richtung. Der Gradient hat auch Darstellungen bezüglich anderer Koordinaten, welche zumeist in der Physik betrachtet werden.

Darstellung in Zylinderkoordinaten:

$V = V\left( {r;\varphi ;z} \right)$

$\operatorname{grad}\, V = \nabla V = \frac{{\partial V}}{{\partial r}}\vec e_r + \frac{1}{r}\frac{{\partial V}}{{\partial \varphi }}\vec e_\varphi + \frac{{\partial V}}{{\partial z}}\vec e_z$

Darstellung in Kugelkoordinaten:

$V = V\left( {r;\vartheta ;\varphi } \right)$

$\operatorname{grad}\, V = \nabla V = \frac{{\partial V}}{{\partial r}}\vec e_r + \frac{1}{r}\frac{{\partial V}}{{\partial \vartheta }}\vec e_\vartheta + \frac{1}{{r\sin \vartheta }}\frac{{\partial V}}{{\partial \varphi }}\vec e_\varphi$

Dies sind Spezialfälle des Gradienten auf Riemann'schen Flächen. Für diese Verallgemeinerung schaue hier nach.

Geometrische Interpretation

Geometrisch betrachtet ist der Gradient eines Skalarfelds an einem Punkt ein Vektor, der in Richtung des steilsten Anstieges des Skalarfeldes weist. Dabei entspricht der Betrag des Vektors der Stärke des Anstieges. Befindet man sich an einem lokalen Minimum oder Maximum (Extremum) oder einem Sattelpunkt, so ist der Gradient an dieser Stelle gerade der Nullvektor, vorausgesetzt, dass dieser Extrempunkt im Inneren des betrachteten Gebietes liegt.

Mit Hilfe des Gradienten lässt sich auch der Anstieg in jeder beliebigen Richtung ermitteln. Dieser Anstieg wird auch Richtungsableitung genannt.

Richtungsableitung

Hauptartikel: Richtungsableitung

Unter der Richtungsableitung versteht man die Ableitung, also den Anstieg eines Skalarfeldes 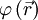$\varphi\left(\vec r\right)$ in Richtung eines normierten Vektors $\vec v$, genauer

$D_{\vec v} \varphi = \frac{\partial\varphi}{\partial\vec v}=\lim_{t\to 0}\frac{\varphi(\vec r+t\vec v)-\varphi(\vec r)}t.$

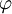Ist ${} \varphi$ in einer Umgebung von 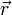$\vec r$ differenzierbar, dann kann man die Richtungsableitung berechnen als das Skalarprodukt aus $\vec v$ und dem Gradienten von $\varphi$.

$D_{\vec v} \varphi = {{\partial\varphi} \over {\partial\vec v}}=\left\langle\mathrm{grad}\varphi{,}\vec v\right\rangle$

Jacobi-Matrix eines Vektorfeldes

Der Vektor der partiellen Ableitungen kann auch für vektorwertige Funktionen definiert werden. Ist 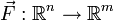$\vec F:\mathbb R^n\rightarrow\mathbb R^m$ eine vektorwertige Funktion, dann seien 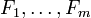$F_1,\ldots,F_m$ ihre Komponentenfunktionen, das heißt

$\vec F(x_1,\ldots,x_n) = \bigl(F_1(x_1,\ldots,x_n), \ldots, F_m(x_1,\ldots, x_n)\bigr)$.

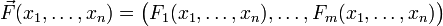Man definiert dann die Ableitung von 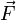${} \vec F$ als (Spalten-)Vektor der (Zeilenvektor-)Gradienten der F_i. Der Vektorgradient des Feldes ist die Jacobi-Matrix.

$\mathcal J_{\vec F}=\operatorname{grad}\vec F=\nabla\vec F= {{\partial (F_1,\ldots,F_m)} \over {\partial (x_1,\ldots,x_n)}}= \begin{pmatrix} \frac{\partial F_1}{\partial x_1}&\cdots&\frac{\partial F_1}{\partial x_n}\\ \vdots&\ddots&\vdots\\ \frac{\partial F_m}{\partial x_1}&\cdots&\frac{\partial F_m}{\partial x_n} \end{pmatrix}$

Für m = n ist das Ergebnis ein Tensor der 2. Stufe. Tensoren dieser Art spielen beispielsweise bei der Beschreibung mechanischer Spannung und Elastizität eine Rolle.

Rechenregeln

Für alle Konstanten 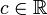$c\in\R$ und Skalarfelder 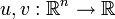$u,v:\R^n\to\R$ gilt:

• $\operatorname{grad}\,c=\vec{0}$

Linearität

• $\operatorname{grad}\,(c\cdot u)=c\cdot\operatorname{grad}\,u$
• $\operatorname{grad}\,(u+v)=\operatorname{grad}\,u+\operatorname{grad}\,v$

Produktregel

• $\operatorname{grad}\,(u\cdot v) = u\cdot\operatorname{grad}\,v + v\cdot\operatorname{grad}\,u$

Anwendung

Vollständiges oder totales Differential eines Skalarfeldes

$\mathrm d \varphi = \frac{\partial\varphi}{\partial x} \mathrm{d} x + \frac{\partial\varphi}{\partial y}\mathrm{d} y + \frac{\partial\varphi}{\partial z} \mathrm{d}z = \operatorname{grad}\,\varphi\;\mathrm{d}\vec{r},\qquad\text{wobei}\quad \mathrm{d}\vec{r} = \begin{pmatrix}\mathrm{d}x\\\mathrm{d}y\\\mathrm{d}z\end{pmatrix}.$

Den Gradienten in allgemein orthogonalen Koordinaten bekommt man mit dem allgemein formulierten Nablaoperator:

$\vec{\nabla} = \sum_{a}{\vec{{e}}_{q_a}\frac{1}{h_a}\frac{\partial}{\partial{q_a}}},\qquad\text{wobei}\quad h_a = \left| {\frac{\partial{\vec{r}}}{\partial{q_a}}}\right|.$

Weitere Beispiele

Sind Teile eines Körper unterschiedlich heiß, so strömt Wärme von den heißeren zu den kühleren Bereichen. Ist die Wärmeleitfähigkeit überall gleich, so ist der Wärmestrom ein Vielfaches des Temperaturgradienten.

Der Druckgradient ist das Verhältnis von Druckdifferenz und dem Abstand zweier Punkte. Bei Richtmikrofonen im Schallfeld hat dieser Begriff eine besondere Bedeutung.

Literatur

• Adolf J. Schwab: Begriffswelt der Feldtheorie, Springer Verlag, ISBN 3-540-42018-5
• Konrad Königsberger: Analysis 2. Springer-Verlag, Berlin/Heidelberg, 2000, ISBN 3-540-43580-8

Weblinks

• Druckgradient und Schallschnelle sind nicht das Gleiche (PDF)
• Wie "krümme" ich Nabla und Delta? – Herleitung des Nablaoperators für orthonormal krummlinige Koordinaten auf www.matheplanet.com