Satz von Bezout

In der Algebraischen Geometrie beschreibt der klassische Satz von Bézout die Anzahl der Schnittpunkte ebener algebraischer Kurven. Er wurde von Étienne Bézout im 18. Jahrhundert formuliert und (im Rahmen der laxeren Ansprüche jener Zeit) bewiesen.

Aussage

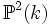Sei k ein algebraisch abgeschlossener Körper und seien F und G zwei projektive ebene Kurven im zweidimensionalen projektiven Raum $\mathbb{P}^2(k)$ ohne gemeinsame Komponenten. Dann gilt:

$\sum_{P\in \mathbb{P}^2(k)} I(P, F \cap G) =\deg F \cdot \deg G,$

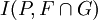wobei $I(P, F \cap G)$ die Schnittzahl bezeichnet.

Folgerungen

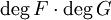• Zwei projektive ebene Kurven F und G schneiden sich immer in mindestens einem Punkt und maximal in $\deg F \cdot \deg G$ verschiedenen Punkten.
• Für affine ebene Kurven F und G ohne gemeinsame Komponenten gilt die Ungleichung $\sum_{P\in k^2} I(P, F \cap G) \leq \deg F \cdot \deg G$.

Verallgemeinerung

Eine Verallgemeinerung für algebraische Varietäten lautet wie folgt:

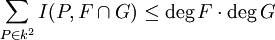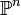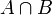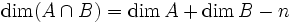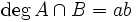Seien A, B algebraische Varietäten vom Grad degA = a bzw. degB = b im n-dimensionalen projektiven Raum $\mathbb P^n$. Ferner sei $A \cap B$ eine Varietät der Dimension $\dim(A\cap B) = \dim A + \dim B -n$.

Dann ist $\deg A\cap B = ab$.

Weblinks