Sektorformel von Leibniz

Kurve mit Fahrstrahl

geschlossene Kurve mit Fahrstrahl

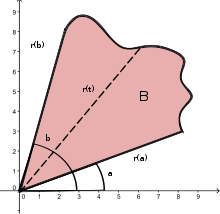
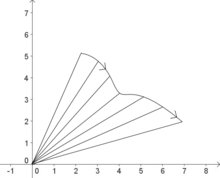
Die Sektorformel von Leibniz, benannt nach Gottfried Wilhelm Leibniz, berechnet den orientierten Flächeninhalt, den ein Fahrstrahl eines Kurvenabschnitts überstreicht, insbesondere kann man mit ihr Flächeninhalte von Gebieten, die durch eine geschlossene Kurve beschrieben werden, berechnen.

Sei $\gamma:[a,b]\rightarrow \mathbb{R}^2$ mit $t\mapsto (x(t),y(t))$ eine glatte Kurve, dann überstreicht ihr mit dem Ursprung gebildeter Fahrstrahl den orientierten Flächeninhalt F der folgenden Größe:

$F(\gamma)=\frac{1}{2}\int_a^b (x(t)y^{\prime}(t)-y(t)x^{\prime}(t))dt$

Stückweise glatte Kurven

Ist γ eine stückweise glatte Kurve auf [a,b] und $\{t_0,\ldots,t_n\}$ eine Partition von [a,b], so dass γ auf den Teilintervallen [t_{k − 1},t_k] für $t=1,\ldots n$ glatt ist, so gilt:

$F(\gamma) = F(\gamma_1)+\ldots+F(\gamma_n)$

Hierbei bezeichnet γ_k die auf das Intervall [t_{k − 1},t_k] beschränkte Kurve.

Zusammenhang mit Dreiecken

Dreieck als stückweise glatte Kurve

Man kann die Sektorformel als eine Verallgemeinerung der Determinantenformel zur Berechnung des Flächeninhaltes von Dreiecken auffassen. Sind A = (x₁,y₁), B = (x₂,y₂), C = (x₃,y₃) die Eckpunkte eines beliebigen Dreiecks, dann wird dieses durch die folgende stückweise glatte Kurve $[0,3]\rightarrow \mathbb{R}^2$ beschrieben:

$\gamma(t):=\begin{cases} \gamma_a(t)=(x_1+(x_2-x_1)t,y_1+(y_2-y_1)t)&\text{falls } 0\leq t\leq 1\\ \gamma_b(t)=(x_2+(x_3-x_2)(t-1),y_2+(y_3-y_2)(t-1))&\text{falls } 1\leq t\leq 2\\ \gamma_c(t)=(x_3+(x_1-x_3)(t-2),y_3+(y_1-y_3)(t-2))&\text{falls } 2\leq t\leq 3 \end{cases}$

Dann gilt nun für die Flächenberechnung des Dreiecks:

$\begin{align} F(\triangle) &= \frac{1}{2}\left |\begin{matrix} 1&x_1&y_1 \\ 1&x_2&y_2 \\ 1&x_3&y_3 \end{matrix} \right | = \frac{1}{2}[(x_1y_2-y_1x_2)+(x_2y_3-y_2x_3)+(x_3y_1-y_3x_1)] \\ &=\quad \frac{1}{2}\int_0^1[(x_1+(x_2-x_1)t)(y_2-y_1)-(y_1+(y_2-y_1)t)(x_2-x_1)]dt \\ &\quad + \frac{1}{2}\int_1^2[(x_2+(x_3-x_2)(t-1))(y_3-y_2)-(y_2+(y_3-y_2)(t-1))(x_3-x_2)]dt \\ &\quad + \frac{1}{2}\int_2^3[(x_3+(x_1-x_3)(t-2))(y_1-y_3)-(y_3+(y_1-y_3)(t-2))(x_1-x_3)]dt \\ &=F(\gamma_a)+F(\gamma_b)+F(\gamma_c)\\ &=F(\gamma) \end{align}$

Zusammenhang mit den Integralsätzen

Für den Fall einer geschlossen Kurve ergibt sich die Sektorformel von Leibniz auch als Spezialfall des Integralsatzes von Green. Der Integralsatz liefert für die von einer Kurve $\gamma:[a,b]\rightarrow\mathbb{R}^2$ mit γ(a) = γ(b) eingeschlossene Fläche B und zwei differenzierbare Funktionen $f,g:\mathbb{R}^2\rightarrow\mathbb{R}$ die folgende Gleichung

$\int_B \Bigl[g_x(x,y)-f_y(x,y)\Bigr] dx dy = \int_a^b \Bigl[f\bigl(x(t),y(t)\bigr)\cdot x^{\prime}(t) + g\bigl(x(t),y(t)\bigr)\cdot y^{\prime}(t)\Bigr] dt$

Wählt man für die dortigen Funktionen f(x,y) = − y und g(x,y) = x, so gilt f_x(x,y) = 1 und g_y(x,y) = − 1 und man erhält:

$\begin{align} &\int_B (1-(-1)) dx dy =\int_a^b \Bigl[-y(t)\cdot x^{\prime}(t) + x(t)\cdot y^{\prime}(t)\Bigr]dt \\ \Leftrightarrow &\int_B 1 dx dy =\frac{1}{2} \int_a^b \Bigl[x(t)\cdot y^{\prime}(t)-y(t)\cdot x^{\prime}(t)\Bigr] dt \end{align}$

Da die Integration über eine Fläche mit 1 den Flächeninhalt selbst liefert, gilt:

$F(\gamma)=\int_B 1 dx dy =\frac{1}{2} \int_a^b \Bigl[x(t)\cdot y^{\prime}(t)-y(t)\cdot x^{\prime}(t)\Bigr] dt$.

Alternative Formel

Alternative Formel

In der Literatur wird gelegentlich auch eine weitere Formel als Sektorformel von Leibniz bezeichnet. Diese ist wesentlich spezieller und verwendet statt Koordinatenfunktionen x(t) und y(t) der Parameterkurve γ(t) eine Funktion r(t), die den Abstand eines Kurvenpunktes vom Zentrum einer sternförmigen Menge B beschreibt.

$F(B)=\frac{1}{2}\int_a^b r(t)^2 dt$

Da diese Formel im Gegensatz zur vorherigen keinen orientierten Flächeninhalt verwendet, ist sie nur für sternförmige Mengen gültig. Ist (x_z,y_z) ein Zentrum der sternförmigen Menge, so lässt sich r(t) mittels der Beziehung $r(t)=\sqrt{(x(t)-x_z)^2+(y(t)-y_z)^2}$ aus den Koordinatenfunktionen der Parameterkurve berechnen.

Beispiel

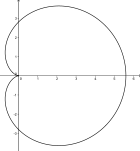
Eine Herzkurve $\gamma:[0,2\pi]\rightarrow \mathbb{R}^2$ besitzt die folgende Parameterdarstellung:

$x = a \cos(t) (1 + \cos(t)) \qquad y = a \sin(t) (1 + \cos (t))$

Mit der Sektorformel ergibt sich dann der folgende Flächeninhalt:

$\begin{align} F(\gamma)&=\frac{1}{2}\int_0^{2\pi}\Bigl[a \cos(t) (1 + \cos(t))a(\cos(t)+2\cos(t)^2-1)+ a\sin(t)(1+2\cos(t))a \sin(t)(1 + \cos (t))\Bigr]dt \\ &=\frac{1}{2}\int_0^{2\pi}\Bigl[(1+\cos(t))^2a^2\Bigr]dt \\ &=\frac{3}{2}a^2\pi \end{align}$

Herzkurve

Bei der Verwendung der alternativen Formel, kann man (0,0) als Zentrum wählen und erhält dann:

$\begin{align} F(\gamma)&=\frac{1}{2}\int_0^{2\pi}\Bigl[\bigl(a \cos(t) (1 + \cos(t))\bigr)^2 +\bigl(a \sin(t) (1 + \cos(t))\bigr)^2\Bigr]dt \\ &=\frac{1}{2}\int_0^{2\pi} \Bigl[(1+\cos(t))^2a^2 (cos(t)^2+sin(t)^2)\Bigr] dt \\ &=\frac{1}{2}\int_0^{2\pi}\Bigl[(1+\cos(t))^2a^2\Bigr]dt \\ &=\frac{3}{2}a^2\pi \end{align}$

Siehe auch

• Regel von Sarrus

Literatur

• Konrad Köngisberger: Analysis 1. 2-te Auflage, Springer 1992, ISBN 3-540-55116-6, S.343
• Harro Heuser: Lehrbuch der Analysis - Teil 2. 5-te Auflage, Teubner 1990, ISBN 3-519-42222-0, S. 498

Weblinks

• Stefan Wilhelm: Leibniz’sche Sektorformel und Rotationsvolumina. Proseminar-Arbeit, Uni Dortmund
• J. Weikert: Kurven und Bogenlänge. In Mathematik für Informatiker I, Skript Uni Saarland
• Mehrdimensionale Integralrechnung. In Höhere Mathematik II (Uni-Skript)