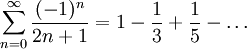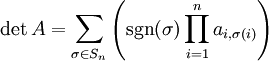Gottfried Wilhelm Freiherr von Leibniz

Gottfried Wilhelm Leibniz Porträt von B. Chr. Francke, um 1700; Herzog Anton Ulrich-Museum

Gottfried Wilhelm Leibniz (* 21. Juni^jul./ 1. Juli 1646^greg. in Leipzig; † 14. November 1716 in Hannover) war ein deutscher Philosoph und Wissenschaftler, Mathematiker, Diplomat, Physiker, Historiker, Politiker, Bibliothekar und Doktor des weltlichen und des Kirchenrechts. Er gilt als der universale Geist seiner Zeit und war einer der bedeutendsten Philosophen des ausgehenden 17. und beginnenden 18. Jahrhunderts. Im 18. Jh. wird er vielfach als Freiherr bezeichnet; doch bislang fehlt eine Beurkundung über die Erhebung in den Adelsstand.

Leben

Gottfried-Wilhelm-Leibniz-Denkmal in Leipzig

Leibniz wurde nach heutigem Kalender am 1. Juli 1646 in Leipzig geboren. Seine Eltern, insbesondere sein Vater, der aus Altenberg/Erzgeb. stammende Rechtsgelehrte Friedrich Leibniz, weckten früh ein Interesse an juristischen und philosophischen Problemen. Sein Vater war Jurist und Professor für Moralphilosophie (Ethik) und seine Mutter Tochter eines Rechtswissenschaftlers. Der achtjährige Leibniz erlernte anhand der umfangreichen väterlichen Bibliothek autodidaktisch die lateinische und die griechische Sprache. Zwölfjährig entwickelte er beim Durchdenken logischer Fragestellungen die Anfänge einer mathematischen Zeichensprache.

1661 immatrikulierte sich Leibniz an der Leipziger Universität und betrieb philosophische Studien beim Theologen Johann Adam Schertzer und dem Philosophietheoretiker Jakob Thomasius. 1663 wechselte er an die Universität von Jena, um sich dort unter Anleitung des Mathematikers, Physikers und Astronomen Erhard Weigel pythagoreischen Gedanken zu öffnen. Mit 20 Jahren wollte er sich zum Doktor der Rechte promovieren lassen, doch die Leipziger Professoren lehnten ihn als zu jung ab. Leibniz ging nach Nürnberg, um dort an der Universität Altdorf das Verwehrte nachzuholen. Vorübergehend stand er in Verbindung zu einer dortigen alchimistischen Geheimgesellschaft, deren Experimente er jedoch schon bald verspottete. Anschließend stand er bis 1672 im Dienst des Mainzer Erzbischofs Johann Philipp von Schönborn.

1672 reiste Leibniz als Diplomat nach Paris. Dort unterbreitete er dem „Sonnenkönig“ Ludwig XIV. einen Plan für einen kreuzzugsähnlichen Eroberungsfeldzug gegen Ägypten, um ihn von den geplanten Eroberungskriegen in Europa abzubringen. Der König lehnte diesen Plan ab; über einhundert Jahre später jedoch setzte Napoléon Bonaparte ihn in der Ägyptischen Expedition um. 1672/73 vollendete Leibniz Arbeiten an einer Rechenmaschine für die vier Grundrechenarten und wurde Mitglied der Londoner „Royal Society“. 1676 wurde er Hofrat und Hofbibliothekar in Hannover und bezog 1698 das heute nach ihm benannte Leibnizhaus in Hannover. 1691 wurde er auch Bibliothekar der Herzog-August-Bibliothek in Wolfenbüttel. Ab 1685 reiste Leibniz im Auftrag des Welfenhauses durch Europa, um eine Geschichte der Welfen zu schreiben. Dadurch hatte er 1688 die Gelegenheit zu einer Audienz bei Kaiser Leopold I. in Wien. Dabei trug Leibniz seine Pläne für eine Münzreform, zum Geld-, Handels- und Manufakturwesen, zu der Finanzierung der Eroberungskriege gegen die Türken, zum Aufbau eines Reichsarchives und vieles andere vor. Doch es wurde ihm nur wohlwollende Aufmerksamkeit zuteil.

Grab in der Neustädter Kirche, Hannover

1700 wurden nach Verhandlungen mit dem brandenburgischen Kurfürsten Friedrich III., dem späteren König Friedrich I., Pläne für eine Preußische Akademie der Wissenschaften nach englischem und französischem Vorbild in die Tat umgesetzt. Die Akademie wurde in Berlin gegründet, Leibniz wurde ihr erster Präsident. Um diesen Erfolg auszudehnen, führte er 1704 in Dresden Verhandlungen über die Gründung einer sächsischen Akademie.

Gottfried Wilhelm Leibniz wurde 1707 von Kaiser Karl VI. geadelt (Freiherrenstand), fiel jedoch kurz vor seinem Tod in Ungnade^[1]. Er bereiste Zeit seines Lebens Europa und knüpfte stets Kontakte zu anderen Wissenschaftlern.

Im Jahr 1716 verbrachte Leibniz einen Kuraufenthalt in Bad Pyrmont. Leibniz starb vereinsamt am 14. November 1716 im Alter von 70 Jahren in Hannover - nur sein Sekretär war beim Begräbnis anwesend^[1] -, und wurde dort in der Neustädter Hof- und Stadtkirche St. Johannis beigesetzt.

Letzter Universalgelehrter

Als Jurist, Naturwissenschaftler, Politiker, Philosoph, Historiker, Theologe und Diplomat sagte Leibniz über sich selbst: „Beim Erwachen hatte ich schon so viele Einfälle, dass der Tag nicht ausreichte, um sie niederzuschreiben.“

Er wuchs in die Zeit der Aufklärung hinein und wird oft als letzter Universalgelehrter bezeichnet. Seine Entdeckungen in den Naturwissenschaften und seine philosophischen und historischen Schriften werden bis heute von Gelehrten aller Welt zu Rate gezogen. Er repräsentierte als letzter großer Denker die vor dem 18. Jahrhundert praktizierte Wissenschaft der vielfältigen Verknüpfung und des Analysierens der Zusammenhänge.

Einige seiner Forschungsergebnisse und Initiativen waren:

• Erfindung des Dualsystems
• Entwicklung der Dezimalklassifikation
• Pläne für ein Unterseeboot
• Verbesserung der Technik von Türschlössern
• Gerät zur Bestimmung der Windgeschwindigkeit
• Rat an Ärzte zur regelmäßigen Fiebermessung
• Gründung einer Witwen- und Waisenkasse
• Beweis für das Unbewusste des Menschen
• Infinitesimalrechnung (Integralrechnung und Differentialrechnung)
• Matrizen und Determinanten
• Erfindung der Staffelwalze für eine mechanische Rechenmaschine
• Als Freund, Fachkollege und Ermunterer der damaligen europäischen Schriftgelehrten und Verfasser sprachkundlich einflussreicher Schriften, war er einer der wesentlichen Initiatoren zur Begründung der modernen Sprachwissenschaft, insbesondere der Indogermanistik.

Philosophie, Religion und Zahl

Leibniz betrachtete die Wissenschaft als eine Einheit. Seine Erkenntnisse in der Integralrechnung, die Theorie der unendlichen Reihen, seine neuartige Geometrie, die Theorien der Kombinatorik, die Vorstellung über die Grundlagen der Mathematik und die Wahrscheinlichkeitsrechnung entwickelten sich in enger Verbindung mit seinen philosophischen Ansichten. Das gleiche trifft auf seine Erkenntnisse der Dynamik, auf die biologischen und geologischen Konzeptionen sowie auf die Forschungen im Bereich der praktischen Politik und der theoretischen Geschichtswissenschaft zu.

Das philosophische Schaffen von Leibniz gruppiert sich um drei große Problemkreise: die Monadentheorie, die Determinationskonzeption und den erkenntnistheoretisch-logischen Ansichten.

Philosophie

Beleuchtetes Leibniz-Zitat am Historischen Museum Hannover

Leibniz hat sein Denken kontinuierlich revidiert. Eine komprimierte Darstellung wichtiger Ideen zur Metaphysik findet sich in seiner Monadologie (1714).

(Siehe: Monadentheorie)

Auch das Problem der „Essai de Théodicée“ (1710) erscheint bei Leibniz gelöst. Unsere Welt ist die beste aller möglichen Welten, sie besitzt einen maximalen Reichtum von Momenten und in diesem Sinne die größtmögliche Mannigfaltigkeit.

In seiner Begriffslehre geht Leibniz davon aus, dass sich alle Begriffe auf einfache, atomare Konzepte zurückführen lassen. Er beschäftigte sich damit, wie man diesen Konzepten Zeichen zuordnen könnte und so wiederum daraus alle Begriffe ableiten könnte. So ließe sich eine ideale Sprache aufbauen. Neben anderen haben die Philosophen Russell und Wittgenstein diese Idee aufgegriffen und weitergeführt. Mit der Ars combinatoria (1666) versuchte Leibniz eine Wiederaufnahme des Projektes der Heuristik.

Text des Leibniz-Zitates am Historischen Museum Hannover:

„Es gibt nicht Ödes, nichts Unfruchtbares, nichts Totes in der Welt, kein Chaos, keine Verwirrung, außer einer Scheinbaren, ungefähr wie sie in einem Teiche zu herrschen schiene wenn man aus einiger Entfernung eine verworrrene Bewegung und sozusagen ein Gewimmel von Fischen sähe, ohne die Fische selbst zu unterscheiden“

– G.W.L.

Aufklärung

Leibniz zählt zu den Frühaufklärern, die den Grundstein für die Bewegung der Aufklärung, „den Ausgang des Menschen aus seiner selbstverschuldeten Unmündigkeit“ (Immanuel Kant), gelegt haben. Er hatte einen starken Einfluss auf die Aufklärung, die klassische deutsche Philosophie, den deutschen Idealismus und die Literatur der Klassik. Leibniz formuliert früh die Maxime der Verstandesmäßigkeit. Zitat: „Jeder Mensch besitzt Fähigkeiten zur vernünftigen Lebensführung.“ Wenn Religion und Vernunft übereinstimmen, entstünde eine wahrhafte Religion. Leibniz postulierte, alle Gaben können den Menschen verderben, nur die echte Vernunft sei ihm unbedingt heilsam, aber an ihr werde erst dann kein Zweifel mehr haften, wenn sie sich überall gleich klar und gewiss, wie die Arithmetik, erweisen könne. Der Mathematiker Leibniz war im Gefolge des Pythagoras der Auffassung, dass sich in den Zahlen die tiefsten Geheimnisse verbergen. Das heißt, wenn man Vernunft mit Zahlen ausdrücken könnte, wäre der Einwand widerlegt: „Woher weißt du, dass deine Vernunft besser ist als meine? Welches Kriterium hast du für die Wahrheit?“

Logik

Leibniz befasste sich intensiv mit Logik und propagierte erstmals eine symbolische Logik in Kalkülform. Seine Logikkalkül-Skizzen veröffentlichte er allerdings nicht; erst sehr verspätet (1840, 1890, 1903) wurden sie publiziert. Seinen Hauptkalkül entwickelte er in den Generales Inquisitiones von 1686. Er entwarf dort die erste Gleichungslogik und leitete in ihr fast zwei Jahrhunderte vor der Boole-Schule die Gesetze der booleschen Verbandsordnung ab. Innerhalb dieses Kalküls formulierte er die traditionelle Begriffslogik bzw. Syllogistik auf gleichungslogischer Grundlage. Er erfand die Mengendiagramme lange vor Leonhard Euler und John Venn und stellte mit ihnen die Syllogistik dar.^[2]

Das Leibniz'sche Gesetz geht auf ihn zurück.

Rechtswesen

1667 veröffentlichte Leibniz eine Schrift zur Reform des Rechtswesens. Darin fordert er eine Vereinheitlichung der Gesetzeswerke der christlichen Nationen. Er versuchte, in jeder Religion etwas Wahres zu finden und dies in eine große Harmonie, in eine allumfassende allgemeine Religion einzuordnen. Mit diesen Bemühungen begab er sich auf die Ebene eines Erasmus von Rotterdam, der ein ähnliches Ziel hatte, nämlich eine Gelehrtenrepublik zu erschaffen, in der antike und christliche Elemente verbunden werden und zu Toleranz und Humanität führen sollten. Leibniz bemühte sich Zeit seines Lebens um den Frieden. Er versuchte 1670 zu einer Reunion von Katholiken und Protestanten beizutragen. Zwischen 1679 und 1702 führte er Verhandlungen mit den Bischöfen Spinola und Bossuet. Bis 1706 bemühte er sich ergebnislos um einen Zusammenschluss wenigstens der evangelischen Konfessionen. Diesen Bemühungen lag seine Ansicht zu Grunde, dass die Glaubensgemeinschaft eine unerlässliche Voraussetzung für die Bewahrung der abendländischen Kultur sei. Alle seine Anstrengungen konnten den Eigensinn der tief voneinander getrennten Länder nicht überwinden. Daran scheiterte Leibniz' Streben nach Synthese und Harmonie.

Harmonie

Synthese bedeutet die Vereinigung von Teilen zu einem Ganzen, die Verbindung gegensätzlicher Dinge zu etwas Neuem. Harmonie ist ein prägender Begriff von Leibniz' Philosophie. Er beschreibt Harmonie als Summe von unendlich vielen, unendlich kleinen Krafteinheiten, sogenannten Monaden, den Urbestandteilen der Weltsubstanz, die durch Gott vereint wurden und so die Welt zusammenhalten.

Leibniz geht davon aus, dass Gott alles aus dem Nichts geschaffen hat (creatio ex nihilo) und alles, was Gott geschaffen hat, gut ist. Daraus ergibt sich die Schlussfolgerung, dass überall eine wunderbare Ordnung zu finden ist. Als Beispiel nennt er die Zahlen, da dort keine Veränderungen vorgenommen wurden.

Dieses Sinnbild des christlichen Glaubens wollte Leibniz sogar zur Heidenbekehrung einsetzen. „Alles weltliche Übel entsteht aus dem endlichen Wesen der Natur.“ Doch die Erkenntnis, dass die Welt in ihrer Unvollkommenheit ein notwendiges Teilübel und dadurch die bestmögliche aller Welten ist, macht den Vorwurf an das Gotteswerk Natur wieder wett. Diese Wissenschaft nannte Leibniz Theodizee.

Monadentheorie

Leibniz entwickelte die Monadentheorie als Gegenentwurf zu den zeitgenössischen Strömungen. Die Philosophen des 17. Jahrhunderts arbeiteten in der Regel entweder eine neue Substanztheorie aus oder sie entwickelten die Atomtheorie nach neuzeitlichen Maßstäben weiter. Leibniz befriedigte keine dieser Auffassungen. Er nennt die Philosophie der Atomisten eine „faule“ Philosophie, da diese Auffassung, welche die Atome als letzte Bausteine ansieht, die lebendige, sich verändernde Welt nicht tiefgründig genug analysiere. Entgegen atomistischer Zeit- und Raumauffassungen, die diese Existenzformen der Materie mit einem leeren Gefäß vergleichen, vertritt Leibniz eine dialektische Konzeption, in der Raum und Zeit Ordnungsbeziehungen in der materiellen Welt sind. Der Raum ist die Ordnung der zur gleichen Zeit existierenden Dinge, die Zeit die Ordnung ihrer kontinuierlichen Veränderungen.

Den Monadenbegriff greift er aus der neuplatonischen Tradition auf. Der Begriff Monade, „Einheit“, stammt aus der Stoicheiosis theologike des spätantiken Philosophen Proklos. Wenn man die unendliche Substanz Baruch de Spinozas und des Mathematikers Blaise Pascal in unzähligen Punkten repräsentiert findet, deren jeder das Universum enthält, dann hat man ein Bild für das Bewusstsein, das in seinem Ichpunkt das ganze All umfasst: dann hat man die Leibnizschen Monaden.

Eine Monade – der zentrale Begriff der Leibnizschen Welterklärung – ist eine einfache, nicht ausgedehnte und daher unteilbare Substanz, die äußeren mechanischen Einwirkungen unzugänglich ist.

Das gesamte Universum bildet sich in den von den Monaden spontan gebildeten Wahrnehmungen (Perzeptionen) ab. Sie sind eine Art spirituelle Atome, ewig, unzerlegbar, einzigartig. Die Idee der Monade löst das Problem der Wechselwirkung von Geist und Materie, welches dem System René Descartes' entspringt. Ebenso löst sie das Problem der Vereinzelung, welches im System Baruch Spinozas problematisch erscheint. Dort werden einzelne Lebewesen als bloß zufällige Veränderungen der einzigen Substanz beschrieben. Ein Beispiel: Eine Substanz kann ohne Denken existieren, aber das Denken nicht ohne Substanz.

Da Leibniz die Grundfrage der Philosophie idealistisch löst und die Materie für ihn nur ein „Anderssein der Seele“ ist, verwirft er den absoluten Charakter von Raum und Zeit. Raum und Zeit werden in der Leibnizschen Metaphysik als Ordnungsbeziehungen zwischen Entitäten der materiellen Welt verstanden. Die Theorie der Substanz von Leibniz schließt die Möglichkeiten der allseitigen Entwicklungen ein. Obwohl die Monaden in ihren Keimen identisch sind, entwickeln sie sich verschieden. Entwicklung bedeutet nach Leibniz nicht das Entstehen von grundsätzlich Neuem, sondern nur die Entfaltung des Vorhandenen. Leib, Seele und Geist sind nicht grundsätzlich verschieden, sie sind bloß unterschiedlich entwickelt. Leibniz löst das Problem der Verbindung von Körper und Seele, indem er darlegt, dass alle Monaden, obwohl sie keinen gegenseitigen Einfluss auf ihre innere Struktur ausüben, koordiniert wirken. Er behauptet, dass Gott beim Schaffen der Monaden ihre Einheit und koordinierte Wirkung gesichert habe. Er kennzeichnet diesen Zustand mit dem Begriff der „prästabilierten Harmonie“. Trotz des idealistisch-teleologischen Wesens dieser Anschauung ist das Bemühen zu spüren, die Einheit der Welt nachzuweisen und die in ihr wirkenden Gesetzmäßigkeiten aufzudecken.

Weltverständnis

Zentrale Begriffe im Leibniz'schen Weltverständnis sind die:

Prästabilierte Harmonie

Es gibt nur die Monaden und ihre Vorstellungen, sonst nichts. Monaden sind unteilbar, und können deswegen nicht in Wechselwirkung miteinander treten. Die Monaden haben aufeinander keinerlei Wirkung. Jede Monade existiert für sich und aus sich. Warum wirken dann aber die Monaden im Weltganzen auf so offensichtliche Weise zusammen? Wieso bilden sie das harmonische Ganze der Welt? Antwort: Gott hat zu Beginn der Welt die Monaden, die aus der Urmonade Gott hervorgegangen sind, so geschaffen, dass sie, wenn jede einzelne nur ihren eigenen Gesetzen folgt, sie alle so zusammenwirken, als ob sie eine Wirkung aufeinander hätten. Die Harmonie war also von vornherein festgelegt.

Theodizee

Der Begriff Theodizee kommt aus dem Griechischen und bedeutet wörtlich etwa "göttliche Gerechtigkeit". Entsprechend rechtfertigen die Überlegungen der Theodizee Gott gegenüber dem menschlichen Vorwurf, für die physischen und metaphysischen Übel und das Böse in der Welt verantwortlich zu sein.

Nach Leibniz hat Gott die aktuale Welt dezidiert ausgewählt und dabei alle Objekte und Ereignisse in ihr mit unendlich vielen anderen möglichen Welten verglichen. Da Leibniz vollständige Determination auf physischer wie mentaler Ebene lehrt und keine Verursachungsbeziehungen zwischen beiden Ebenen zulässt (seine sog. These der prästabilierten Harmonie), scheint einzig Gott für das Übel in der Welt verantwortlich zu sein, denn er ist es, der sich für diese Welt entschieden hat - die allerdings nach Gottes Ansicht die bestmögliche war.

Beste aller möglichen Welten

Der berühmte Satz von der „besten aller möglichen Welten“ ist oft missverstanden worden, unter anderem hat ihm Voltaire mit dem Candide einen ganzen Spottroman gewidmet. Die Idee der „besten aller möglichen Welten“ soll nicht in naiver Weise tatsächliches und großes Übel in der Welt leugnen oder schönreden. Vielmehr wird von Leibniz auf einen notwendigen Zusammenhang zwischen Gutem und Üblem hingewiesen. Es gäbe nämlich Gutes, das nur zum Preis der Existenz von Übel zu haben ist. Die wirkliche Welt ist die beste u. a. in dem Sinne, dass das Gute in ihr auch von Gott nicht mit einem geringeren Maß an Übel verwirklicht werden kann. Außerdem ist die „beste aller möglichen Welten“ dynamisch gedacht: Nicht der derzeitige Zustand der Welt ist der bestmögliche, sondern die Welt mit ihrem Entwicklungspotential ist die beste aller möglichen Welten.

Gerade dieses Entwicklungspotential ermöglicht es, den derzeitigen Zustand zu verbessern, nicht hin auf einen utopischen Endpunkt, sondern immer weiter, in einem nicht endenden Prozess der ständigen sich überbietenden Entwicklung.

Leibniz argumentiert einerseits, dass einige der Übel nur scheinbar sind, bzw. dass weniger Übel an einer Stelle ein mehr an anderer Stelle notwendig machen würde. Auch führt er zum Beispiel die Vielfalt an, die die Qualität der Welt ausmache. Es gibt aber auch einen logischen Grund, warum diese die beste aller möglichen Welten sein muss. Wenn nämlich Gott eine Welt aus dem Möglichen ins Wirkliche überführen möchte, so braucht er einen zureichenden Grund, da er nicht willkürlich wählen kann. Das einzige Kriterium, das eine Welt aber qualitativ von allen anderen unterscheidet, ist, die beste zu sein. Im Gegensatz etwa zu Descartes vertritt Leibniz die Ansicht, dass Gott nicht logische Wahrheiten schaffen oder ändern kann. Die Summe aller möglichen Welten findet Gott ebenso vor wie mathematische Sätze. Er hat darum auf den Zustand und die Geschehnisse innerhalb einer Welt keinen Einfluss. Selbst wenn er - Naturgesetze außer Kraft setzend - ein Wunder wirkt, so ist dieses Wunder mit der Auswahl der möglichen Welt schon ein für allemal festgelegt.

Dass Gott unter allen möglichen Welten die beste geschaffen habe, weil er allmächtig, allwissend und allgütig sei, ist insofern nur ein Teilaspekt. Leibniz unterscheidet dann zwischen drei Übeln:

1. Metaphysisches Übel

Das metaphysische Übel bzw. Elend besteht in der Endlichkeit der Welt. Diese war nicht zu vermeiden, wenn Gott eine Welt schaffen wollte. (Siehe Platon)

2. Physisches Übel

Leiden und Schmerzen gehen mit einer gewissen Notwendigkeit aus dem metaphysischen Übel hervor, da geschaffene Wesen zwangsläufig unvollkommen sind.

3. Moralisches Übel

Ein geschaffenes Wesen hat die Möglichkeit zu fehlen bzw. theologisch formuliert zu sündigen, da Gott ihm die Gabe der Freiheit verliehen hat.

Nach Leibniz gibt es keinen Widerspruch zwischen Determinismus und Freiheit. Obwohl mit der Wahl der Welt jede Handlung eines Menschen zum Beispiel vollständig unverrückbar festliegt, so ist die Tatsache, dass sich ein Mensch in einer Situation so und nicht anders verhält, völlig frei. Dass sich ein Mensch so verhält (so verhalten würde), ist gerade der Grund, warum die Welt gewählt wurde. Ein anderes Verhalten wäre entweder logisch nicht möglich (nicht kompossibel mit dem Rest der Welt) oder würde eine moralisch schlechtere Welt bedingen.

Mathematik

Zahlen aus dem Geist der Religion

Durch die geistige Auseinandersetzung mit der Religion, insbesondere mit dem Yijing-Orakel, das besagt, dass das Universum, die Erde und das All nach Gewicht, Maß und Zahl gezeugt sind, ist es Leibniz möglich ein neues Zahlensystem zu entwickeln. Die Zahl in ihrer metaphysischen Grundgestalt und die Arithmetik als Statik des Universums enthüllen die Kräfte aller Dinge. Für Leibniz gilt die Devise: „Ohne Gott ist nichts.“ Deshalb setzt er für Gott die Eins und für das Nichts die Null. Gleichzeitig untersucht er die Sprache und stellt fest, dass sie ständig Fehler zulässt. Dadurch entstehen enorme Verständigungsprobleme, die über kurz oder lang zu Konflikten führen. Leibniz setzte als Ziel seiner Forschungen die Lösung dieser Konflikte. Er meinte erkannt zu haben, dass unser Denken eigentlich ein Rechenvorgang sei, womit sich der Kreis zur Religiosität und jener von Gott und Nichts, von 1 und 0, schließt. Konsequenterweise versuchte er eine sichere logische Symbolsprache zu entwickeln ('matesis universalis'). Hieraus entstand das Dualsystem, welches in der Natur und Philosophie kein Vorbild hatte. Es bildet die operationale Grundlage der modernen Computertechnik. Außerdem erkannte Leibniz, dass man jedem Gegenstand eine charakteristische Zahl beilegen kann, ähnlich den arithmetischen Zeichen für die natürlichen Zahlen. Damit, so Leibniz, wollte Gott uns zeigen, dass unser Verstand noch ein weit tieferes Geheimnis birgt, von dem die Arithmetik nur ein Schattenbild ist.

Infinitesimalrechnung

Bereits 1672 konstruierte Leibniz eine Rechenmaschine, die multiplizieren, dividieren und die Quadratwurzel ziehen konnte.

Während eines Parisaufenthalts in den Jahren 1672 bis 1676 trat Leibniz in Kontakt zu führenden Mathematikern seiner Zeit. Ohne sichere theoretische Grundlage lernte man damals, unendliche Folgen und Reihen aufzusummieren. Leibniz fand ein Kriterium zur Konvergenz alternierender Reihen (Leibniz-Kriterium), aus dem insbesondere die Konvergenz der sogenannten Leibniz-Reihe

$\sum_{n=0}^{\infty} \frac{(-1)^n}{2n+1} = 1 - \frac{1}{3} + \frac{1}{5}- \dots$

folgt. Mittels geometrischer Überlegungen fand er auch deren Grenzwert 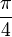$\frac{\pi}4$. Durch Summation von Reihen gelangte Leibniz 1675 zur Integral- und von dort zur Differentialrechnung; er dokumentierte seine Erfindung 1684 mit einer Veröffentlichung in den acta eruditorum. Nach heutigen Maßstäben (Priorität der Erstveröffentlichung) würde er als alleiniger Erfinder der Infinitesimalrechnung gelten; diese Betrachtung ist jedoch anachronistisch, da wissenschaftliche Kommunikation im 17. Jahrhundert primär mündlich und per Briefwechsel erfolgte. Bleibendes Verdienst von Leibniz ist insbesondere die heute noch übliche Notation von Differentialen (mit einem Buchstaben d von lat. differentia), Differentialquotienten (dy/dx) und Integralen (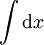$\int \text{d}x$; das Integralzeichen ist abgeleitet aus dem Buchstaben S von lat. summa).

Der englische Naturwissenschaftler Sir Isaac Newton hatte die Grundzüge der Infinitesimalrechnung bereits 1666 entwickelt. Jedoch veröffentlichte er seine Ergebnisse erst 1687. Daraus entwickelte sich Jahrzehnte später der vielleicht berühmteste Prioritätsstreit der Wissenschaftsgeschichte, der bis heute nicht eindeutig entschieden ist: Man kann nicht genau sagen, in welchem Stadium seiner zweifellos eigenständigen Entwicklung Leibniz welche Newton-Briefe gesehen hat und welchen Vorteil er daraus gezogen hat. Die ersten Pamphlete, in denen Leibniz beziehungsweise Newton beschuldigt wurden, den jeweils anderen plagiiert zu haben, erschienen 1699 und 1704. Im Jahr 1711 brach der Streit in voller Schärfe aus. Die Royal Society verabschiedete 1712 einen Untersuchungsbericht, der von Newton selbst fabriziert worden war; Johann Bernoulli antwortete 1713 mit einem persönlichen Angriff auf Newton. Der Streit wurde über Leibniz' Tod hinaus fortgeführt und vergiftete die Beziehungen zwischen englischen und kontinentalen Mathematikern über mehrere Generationen hinweg. Schaden nahm vor allem die Entwicklung der Mathematik in England, die lange an den technisch unterlegenen Newtonschen Notationen festhielt.

Matrix und Dyadik

Bei der Beschäftigung mit der Matrizen-Rechnung fand der Mathematiker die so genannte Leibniz-Formel zur Berechnung der Determinante für eine allgemeine $n \times n$-Matrix:

$\det A = \sum_{\sigma \in S_n} \left(\operatorname{sgn}(\sigma) \prod_{i=1}^n a_{i, \sigma(i)}\right)$

Er entwickelte auch die Dyadik (Dualsystem) mit den Ziffern 0 und 1 (Dualzahlen), die für die moderne Computertechnik von grundlegender Bedeutung ist.

Zur Mathematik gehören auch seine Leistungen im Gebiet der Logik (siehe oben).

Sonstiges

Dresdener Nachbau von Leibniz' Rechenmaschine

Viele bedeutende Erfindungen stammen von Leibniz, zum Beispiel eine Rechenmaschine sowie Erfindungen zur Nutzung des Windes bei der Grubenentwässerung im Oberharzer Bergbau. Leibnizens Rechenmaschine (von der es fünf aufeinanderfolgende Versionen gibt) war ein historischer Meilenstein im Bau von mechanischen Rechenmaschinen. Das von ihm erfundene Staffelwalzenprinzip, mit dem Multiplikationen auf mechanische Weise realisiert werden konnten, hielt sich über 200 Jahre als unverzichtbare Basistechnik. Die feinmechanischen Probleme, die es beim Bau einer solchen Maschine zu überwinden galt, waren jedoch so immens, dass berechtigte Zweifel daran bestehen, ob zu Leibnizens Lebzeiten jemals eine fehlerfrei arbeitende Maschine realisiert werden konnte. Eine fehlerfrei arbeitende Replik nach Leibnizens Konstruktionsplan konnte erst 1990 durch Nikolaus Joachim Lehmann (Dresden) realisiert werden.

Im weiteren Sinne war Leibniz wegbereitend für die Rechenmaschine im heutigen Sinne, den Computer. Er entdeckte, dass sich Rechenprozesse viel einfacher mit einer binären Zahlencodierung durchführen lassen, und ferner, dass sich mittels des binären Zahlencodes die Prinzipien der Arithmetik mit den Prinzipien der Logik verknüpfen lassen. (s. De progressione Dyadica, 1679; oder Explication de l'Arithmetique Binaire, 1703). Die hier erforschten Prinzipien wurden erst 230 Jahre später in der Konstruktion von Rechenmaschinen eingesetzt (z.B. bei der Zuse Z1). Leibniz hatte beim Bau einer Rechenmaschine, anders als frühere Erfinder, eher philosophische Motive. Mit dem viel bemühten Zitat, es sei „ausgezeichneter Menschen unwürdig, gleich Sklaven Stunden zu verlieren mit Berechnungen“, wird eine Grenze zwischen Mensch und Maschine gezogen. Dem Erfindergeist (Freiheit, Spontaneität und Vernunft) als das spezifisch Menschliche wird das Mechanische der technisch-natürlichen Kausalität gegenüber gestellt. Leibniz Erfindung sollte daher eng im Zusammenhang mit den etwa zeitgleich erschienenen Arbeiten zur Monadologie gesehen werden, statt in Verbindung mit praktischen, d.h. kaufmännischen, technischen und mathematischen Interessen.

In seinem 1759 posthum veröffentlichten Werk "Protogaea" gilt Leibniz als Pionier der Höhlenkunde und als Mitbegründer der Paläontologie^[3], da er darin Fossilien nicht als Naturspiele betrachtete, sondern als Versteinerungen früherer Organismen, die durch große Umwälzungen in anderen Teilen der Erde verschwunden seien oder verändert wurden. Leibniz hatte auch erste Vorstellungen zu einem evolutiven Artwandel und vermutete beispielsweise, dass die verschiedenen Raubkatzenarten von einer gemeinsamen ursprünglichen Katzenart abstammen könnten.

Briefe

Brief von Leibniz nach Kiel aus dem März 1716 eine Veröffentlichung betreffend

Leibniz war einer der wichtigsten interdisziplinären Gelehrten seiner Epoche. Ein großer Teil seines Wirkens ist in Briefen dokumentiert. Aus der Zeit zwischen 1663 und 1716 sind über 20.000 Briefe an Leibniz überliefert, die er von rund 1.100 Korrespondenten aus 16 Ländern erhalten hat. Im Leibniz-Archiv sind rund 15.000 Briefe dokumentiert. Er war ein „homo societatis“.

Gedenken

Briefwechsel als Unesco-Weltdokumentenerbe

Das Deutsche Nominierungskomitee hat den in der Gottfried Wilhelm Leibniz Bibliothek in Hannover aufbewahrten Briefwechsel von Gottfried Wilhelm Leibniz 2006 für das UNESCO-Programm Weltdokumentenerbe (Memory of the World) vorgeschlagen. Im Herbst 2007 entschied der Generaldirektor der UNESCO abschließend über den Neueintrag in das Memory of the World-Register. Damit erklärte die UNESCO den Briefwechsel als Bestandteil des Weltgedächtnisses und damit als besonders schützenswert.

Der Briefwechsel enthält rund 15.000 Briefe mit 1.100 Kor­respondenten. Er ist Bestandteil des in Hannover aufbewahrten Leibniz-Nachlasses mit ca. 50.000 Nummern mit rund 200.000 Blättern. Zum Nachlass gehören auch die Bibliothek von Leibniz und das einzig erhaltene Exemplar der von ihm konstruierten Vier-Spezies-Rechen­maschine.

Denkmäler

Leibniz-Denkmal. Unten rechts die Rückseite der Skulptur mit der Darstellung des binären Zahlensystems

In der Nähe der Universität befindet sich das Gottfried-Wilhelm-Leibniz-Denkmal in Leipzig.

Am 27. November 2008 wurde in der Innenstadt von Hannover zum Gedenken an Leibniz ein Denkmal eingeweiht. ^[4] Es handelt sich um eine 2,5 m hohe Bronzeskulptur auf einem Granitsockel, die von 10 Sponsoren für 110.000 Euro gestiftet wurde. Eine Seite bildet das Leibniz-Zitat Unitas in multitudine (Einheit der Vielfalt) ab, die andere Seite zeigt das von Leibniz entwickelte binäre Zahlensystem.

Patronat und Institutionen

• Gottfried-Wilhelm-Leibniz-Universität Hannover (Umbenennung der Universität Hannover am 1. Juli 2006)
• Gottfried Wilhelm Leibniz Bibliothek Hannover
• Wissenschaftsgemeinschaft Gottfried Wilhelm Leibniz
• Leibniz-Sozietät Berlin
• Leibniz Kolleg Tübingen
• Leibniz-Rechenzentrum Garching
• Leibniz-Gymnasien in ganz Deutschland

Preisvergaben

• Gottfried-Wilhelm-Leibniz-Preis
• Leibniz-Ring-Hannover
• Leibniz-Medaille der Berlin-Brandenburgischen Akademie der Wissenschaften
• Leibniz-Medaille der Akademie der Wissenschaften und der Literatur Mainz

Sonstiges

• Leibniz (Mondkrater), bei 38° 18′ S, 179° 12′ O
• Leibniz Butterkeks der „Hannoverschen Cakes-Fabrik H. Bahlsen 1891

Siehe auch

• Prästabilierte Harmonie
• Vernunftwahrheiten und Tatsachenwahrheiten
• Vinculum substantiale
• Sektorformel von Leibniz

Literatur

Werke

• 1686: Metaphysische Abhandlung (Originaltitel: Discours de métaphysique)
• 1704: Neue Abhandlungen über den menschlichen Verstand (Originaltitel: Nouveaux Essais sur L'entendement humain)
• 1710: Theodizee (Originaltitel: Essais de théodicée)
• 1714: Monadologie (Originaltitel: Principes de la Nature et de la Grace fondés en Raison - Monadologie)
• 1759 (posthum): Protogaea oder Abhandlung von der ersten Gestalt der Erde und den Spuren der Historie in Denkmalen der Natur
• Disputatio Metaphysica De Principio Individui. Lipsiae 1663, Online-Ausgabe der Sächsischen Landesbibliothek - Staats- und Universitätsbibliothek Dresden
• Gottfredi Guilielmi Leibnüzii Lipsensis, Ars Combinatoria. [Jena] 1690, Online-Ausgabe der Sächsischen Landesbibliothek - Staats- und Universitätsbibliothek Dresden

Textausgaben

• Gottfried Wilhelm Leibniz Sämtliche Schriften und Briefe, hg. von der Preußischen (jetzt Deutschen) Akademie der Wissenschaften, 1923- Informationen und teils Voreditionen online (wird ergänzt).

• Die philosophischen Schriften von Gottfried Wilhelm Leibniz, hg. C. I. Gerhardt, 7 Bde., 1875-1890 (wiederholt nachgedruckt).
• Leibnizens mathematische Schriften, hg. C. I. Gerhardt, 7 Bde., 1849-1863.
• Opuscules et fragments inédits de Leibniz, hg. Louis Couturat, 1903.
• Textes Inédits, hg. Gaston Grua. Paris: Presses Universitaires de France, 1948.
• Generales inquisitiones de analysi notionum et veritatum, hg. übersetzt und kommentiert von Franz Schupp, Hamburg 1982, ISBN 3-7873-0533-5
• Ermahnung an die Deutschen. Von deutscher Sprachpflege. Unveränderter reprographischer Nachdruck der Ausgabe Leipzig 1916. Wissenschaftliche Buchgesellschaft, Darmstadt 1967 (Libelli 216)
• Discours sur la Théologie Naturelle des Chinois, hrsg. von Wenchao Li und Hans Poser, Frankfurt am Main 2002, ISBN 978-3-465-03214-4

Fremdsprachige Ausgaben

• Allgemeine Untersuchungen über die Analyse der Begriffe und Wahrheiten Lat.-dt., Übers. Franz Schupp, 2. Aufl. Meiner, Hamburg 1993 ISBN 978-3-7873-1142-2
• Specimen Dynamicum. Lat.-dt., Hg. & Übers. Hans Günter Dosch, Glenn W. Most u. Enno Rudolph. Meiner, Hamburg 1982 ISBN 978-3-7873-0534-6
• Philosophische Werke Übers. Artur Buchenau & Ernst Cassirer, 4 Bde. Meiner, Hamburg 1996 ISBN 978-3-7873-1164-4
• Die Grundlagen des logischen Kalküls Lat.-dt., Hg. & Übers. Franz Schupp & Stephanie Weber. Meiner, Hamburg 2000 ISBN 978-3-7873-1601-4
• Monadologie und andere metaphysische Schriften Franz.-Dt., Hg. & Übers. Ulrich Johannes Schneider Meiner, Hamburg 2002 ISBN 978-3-7873-1606-9
• Lehrsätze der Philosophie. MONADOLOGIE. Letzte Wahrheiten über Gott, die Welt, die Natur der Seele, den Menschen und die Dinge. Textausgabe Dt.-Frz., Übers. & fortlfd. dt. Kommentar Joachim Christian Horn. Königshausen & Neumann, Würzburg 1985 ISBN 3213000019 - 2. Aufl. 1997 ISBN 3826012976
• Frühe Schriften zum Naturrecht Lat.-dt., unter Mitwirkung von Hans Zimmermann übers. u. hrsg. v. Hubertus Busche. Meiner, Hamburg 2003 ISBN 978-3-7873-1622-9
• Philosophische Schriften Hg. Hans Heinz Holz. 4 Bände. Suhrkamp, Frankfurt (1986) 1996 ISBN 3-518-09233-2
• Philosophische Schriften und Briefe 1683 - 1687 Hg. Ursula Goldenbaum. Berlin 1992
• Frühe Schriften zum Naturrecht Lat./dt., Phil. Bibl. Bd. 543 ISBN 3-7873-1622-1
• Philosophical Essays. Edited and translated by Roger Ariew and Daniel Garber. Hackett, Indianapolis 1989
• Philosophical Papers and Letters, Hg. Leroy Loemker, 2. Aufl. Reidel, Dordrecht 1969
• Philosophical Writings. Translated and edited by Mary Morris and G.H.R. Parkinson. Dent, London 1973
• Logical Papers. Transl. & Ed. G.H.R. Parkinson. Oxford UP, 1966
• Monadology and Other Philosophical Essays. Translated and edited by Paul Schrecker and Anne Martin Schrecker. Bobbs-Merrill, N. Y. 1965
• Selections Ed. Philip P. Wiener. Charles Scribner's Sons, N. Y. 1951
• Philosophical Texts. Edited and translated by R. S. Woolhouse and Richard Francks. With introduction and notes by R. S. Woolhouse, Oxford UP 1998 ISBN 0-19-875153-2
• Confessio philosophi. Das Glaubensbekenntnis des Philosophen. Ein Dialog Lat.-dt., Hg. & Übers. Otto Saame, Klostermann, Frankfurt 1999 ISBN 978-3-465-02665-5 ISBN 3465026659 (zuerst 1967)
• Leibniz korrespondiert mit China. Der Briefwechsel mit den Jesuitenmissionaren (1689-1714) Hg. Rita Widmaier, Frankfurt 1990 ISBN 978-3-465-02213-8

Einführende Sekundärliteratur

• Karl-Heinz Best: Gottfried Wilhelm Leibniz (1646-1716). In: Glottometrics 9, 2005, S. 79-82. (Thema: Bedeutung von Leibniz für die Quantitative Linguistik.)
• Thomas Leinkauf: Leibniz. Ausgewählt und vorgestellt Reihe: Philosophie jetzt! dtv, München 2000 (zuerst: Eugen Diederichs, ebd. 1996) ISBN 3-423-30691-2 (bis S. 38: Einführung & Lebenslauf. Ab S. 39 - 498 Auszüge aus allen Schriften & Anm. dazu. Ferner: Lit. & ausf. Stichwortverz.)
• Michael-Thomas Liske: Gottfried Wilhelm Leibniz Beck, München 2000 ISBN 3-406-41955-0
• Hans Poser: Gottfried Wilhelm Leibniz zur Einführung Junius, Hamburg 2005 ISBN 3-88506-613-0
• Werner Schneiders: Gottfried Wilhelm Leibniz: Das Reich der Vernunft in: Josef Speck (Hg.): Grundprobleme der großen Philosophen Philosophie der Neuzeit I. Göttingen 1979, S. 139-175

Monographien

Biographie

• Eric J. Aiton: Gottfried Wilhelm Leibniz: eine Biographie. Frankfurt a.M.: Insel, 1991 (Orig. Leibniz. A Biography. Bristol: Hilger, 1985)
• Ines Böger: »Ein seculum … da man zu Societäten Lust hat«. Darstellung und Analyse der Leibnizschen Sozietätspläne vor dem Hintergrund der europäischen Akademiebewegung im 17. und frühen 18. Jahrhundert. Herbert Utz Verlag, München 2001, ISBN 3-8316-0018-X
• Reinhard Finster, Gerd van den Heuvel: Gottfried Wilhelm Leibniz. Mit Selbstzeugnissen und Bilddokumenten. 4. Auflage. Rowohlt, Reinbek bei Hamburg 2000 (Rowohlts Monographien, 50481), ISBN 3-499-50481-2
• Eike Christian Hirsch: Der berühmte Herr Leibniz. Eine Biographie. C. H. Beck, München 2000, ISBN 3-406-45268-X
• Kurt Müller, Gisela Krönert: Leben und Werk von Gottfried Wilhelm Leibniz. Eine Chronik. Klostermann, Frankfurt am Main 1969 (Veröffentlichungen des Leibniz-Archivs, 2)
• G. E. Guhrauer: Gottfried Wilhelm Freiherr von Leibniz: eine Biographie; zu Leibnizens Säkular-Feier; mit neuen Beilagen und einem Register / G.E. Guhrauer. - Hildesheim: Olms
• Gunter Quarg: Gottfried Wilhelm Leibniz (1646-1716) : eine Ausstellung zu Leben und Werk in Büchern und Dokumenten / von Gunter Quarg. - Köln: Universitäts- und Stadtbibliothek, 1996. - 106 S. . - ISBN 3-931596-08-7. - (Kleine Schriften der Universitäts- und Stadtbibliothek Köln ; 1)
• George MacDonald Ross: Gottfried Wilhelm Leibniz. Leben und Denken Leibniz-Bücherwarte, Bad Münder 1990, ISBN 978-3-925237-14-0

Denken

• Robert M. Adams: Leibniz: Determinist, Theist, Idealist, Oxford: Oxford University Press 1998, ISBN 0-19-508460-8.
• J. A. Cover, John O'Leary-Hawthorne: Substance and Individuation in Leibniz, Cambridge: Cambridge University Press 1999, ISBN 0-521-59394-8
• Aron Gurwitsch: Leibniz. Philosophie des Panlogismus, Berlin: Walter de Gruyter 1974, ISBN 3-11-004358-0.
• Nicholas Jolley (Hg.) : The Cambridge Companion to Leibniz, Cambridge: Cambridge University Press 1995, ISBN 0-521-36588-0.
• M. Kulstad: Leibniz on Apperception, Consciousness, and Reflection, München: Philosophia Verlag 1991, ISBN 3-88405-069-9.
• Benson Mates: The philosophy of Leibniz. Metaphysics and language, New York: Oxford Univ. Pr. 1986, ISBN 0-19-503696-4.
• R. McRae: Leibniz: Perception, Apperception, and Thought, Toronto: University of Toronto Press, 1976, ISBN 0-8020-5349-1.
• G. H. Parkinson: Leibniz on Human Freedom. Stuttgart 1970
• Nicholas Rescher: Leibniz, An Introduction to his Philosophy, Oxford: Basil Blackwell 1979, ISBN 0-631-11570-6 .
• Nicholas Rescher: Leibniz's Metaphysics of Nature. A group of essays. Dordrecht: D. Reidel 1981, ISBN 90-277-1252-2.
• Bertrand Russell: A Critical Exposition of the Philosophy of Leibniz, London: Routledge 1992 (1. A. 1900), ISBN 0-415-08296-X.
• Donald Rutherford: Leibniz and the Rational Order of Nature, Cambridge: Cambridge University Press 1995, ISBN 0-521-46155-3.
• Catherine Wilson: Leibniz's Metaphysics: A historical and comparative study, Manchester: Manchester University Press 1989, ISBN 0-7190-2788-8.
• R. S. Woolhouse (Hg.): Gottfried Wilhelm Leibniz. Critical assessments, London: Routledge 1994 (4 Bde.), ISBN 0-415-03808-1
• Wolfgang Lenzen: Calculus universalis. Studien zur Logik von G. W. Leibniz, Paderborn: Mentis 2004, ISBN 3-89785-362-0
• Wolfgang Lenzen: „Leibniz's Logic“, in: Dov M. Gabbay, John Woods (Hge.): Handbook of the History of Logic, Volume 3, The Rise of Modern Logic: from Leibniz to Frege, North-Holland 2004, ISBN 978-0-444-51611-4, Seite 1–83

Einzelnachweise

1. ↑ ^{a b} Kleine Weltgeschichte der Wissenschaft / Hans Joachim Störig. - Zürich : Ex Libris, 1965; S. 252
2. ↑ De Formae Logicae per linearum ductus, ~1690, erst posthum 1903 veröffentlicht in: Couturat: Opuscules et fragmentes inedits de Leibniz, 292-321
3. ↑ Ein Beitrag zur Geschichte der Paläontologie und zur Leibnizforschung
4. ↑ Quelle: hannover.de

Weblinks

• Literatur von und über Gottfried Wilhelm Leibniz im Katalog der Deutschen Nationalbibliothek (Datensatz zu Gottfried Wilhelm Leibniz • PICA-Datensatz • Einträge im Musikarchiv)

• Druckschriften von und über Gottfried Wilhelm Leibniz im VD 17
• Brandon Look: „Gottfried Wilhelm Leibniz“ in der Stanford Encyclopedia of Philosophy (englisch, inklusive Literaturangaben)
• Gottfried Wilhelm Leibniz. In: Allgemeine Deutsche Biographie (ADB). Band 18, Duncker & Humblot, Leipzig 1883, S. 172.
• Gottfried Wilhelm Leibniz. In: Biographisch-Bibliographisches Kirchenlexikon (BBKL).
• Leibniz in WikiLingua
• Leben und Werk Leibniz-Archiv, Hannover
• Datenbank der Niedersächsischen Gottfried Wilhelm Leibniz Bibliothek
• Der Briefwechsel von Gottfried Wilhelm Leibniz, der in der Leibniz-Bibliothek Hannover aufbewahrt ist, wird Weltdokumentenerbe der Unesco.
• Universität Münster Forschungsstelle Leibniz
• Der berühmte Brief vom 12. 1. 1697
• Kurzbiographie bei Landtag Niedersachsen
• Jürgen Lawrenz: Leibniz: Double-Aspect Ontology and the labyrinth of the continuum, Diss. Sydney 2007 (Engl.)
• Informationen zu Leibniz, Gottfried, Wilhelm im BAM-Portal

Werke

• Nachweise von lateinischen Werken im Internet
• Akademie Ausgabe Online
• Werke in Originalsprache (PDF) (Die Ausgaben von Gerhardt, Couturat, Grua und einige weitere)
• Kleine Auswahl in der Biblioteca Augustana
• Physikalische Schriften

Personendaten
NAME	Leibniz, Gottfried Wilhelm
ALTERNATIVNAMEN	Leibniz, Gottfried Wilhelm Freiherr von
KURZBESCHREIBUNG	deutscher Philosoph, universaler Wissenschaftler und Doktor des weltlichen und des Kirchenrechts
GEBURTSDATUM	1. Juli 1646
GEBURTSORT	Leipzig
STERBEDATUM	14. November 1716
STERBEORT	Hannover