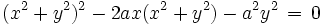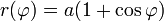Herzkurve

Die Kardioide oder Herzkurve ist eine ebene Kurve, genauer gesagt eine algebraische Kurve 4. Ordnung, die ihren Namen wegen ihrer Form erhielt.

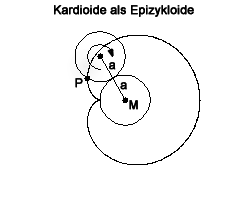
Lässt man auf der Außenseite eines gegebenen festen Kreises mit Mittelpunkt M und Durchmesser a einen weiteren Kreis mit dem gleichen Durchmesser abrollen und betrachtet man dabei einen bestimmten Punkt P auf dem abrollenden Kreis, so beschreibt P eine Kardioide. Damit erweist sich die Kardioide als spezielle Epizykloide.

Gleichungen der Kardioide

• Kartesische Koordinaten:

$(x^2 + y^2)^2 - 2 a x (x^2 + y^2) - a^2 y^2 \, = \, 0$

• Polarkoordinaten:

$r(\varphi) = a (1 + \cos\varphi)$

• Parametergleichung:

$x(t) = a \cos(t) (1 + \cos(t)); \qquad y(t) = a \sin(t) (1 + \cos (t))$

Eigenschaften der Kardioide

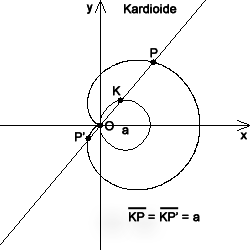
Im Folgenden wird jeweils vorausgesetzt, dass die Koordinatenachsen so liegen wie in der Skizze.

• Die Punkte der Kardioide sind gekennzeichnet durch die folgende geometrische Eigenschaft: Gegeben seien ein Kreis mit Durchmesser a und ein Punkt O auf diesem Kreis. Ist nun K ein von O verschiedener Punkt des Kreises, so liegen die beiden Punkte P und P', die auf der Geraden OK liegen und von K die Entfernung a haben, auf der Kardioide.

• Die Kardioide ist achsensymmetrisch bezüglich der x-Achse. Genau zwei Punkte der Kurve liegen auf der Symmetrieachse, nämlich der Ursprung und der Punkt (2a, 0).
• Die Kardioide schließt eine Fläche mit dem Inhalt 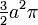$\tfrac{3}{2} a^2 \pi$ ein.
• Die Kurvenlänge beträgt 8a.
• Die Kardioide ist ein Spezialfall der pascalschen Schnecke, diese ist wiederum ein Spezialfall der Konchoide.
• Die Lichterscheinung (Kaustik) in einer Kaffeetasse, die von Licht aus einer am Tassenrand platzierten Lichtquelle getroffen wird, ist eine Kardioide. Die Kaustik, die von parallel eintreffendem Licht erzeugt wird, wird allerdings durch eine andere Kurve (Nephroide) beschrieben; in anderen Fällen entsteht eine Mischform.

In der Tontechnik wird das Polardiagramm der Richtcharakteristik einer Kardioide mit Niere bezeichnet, auch wenn es eine Herzkurve darstellt.