Separabler Hilbertraum

Der mathematische Begriff separabel bezeichnet in der Topologie eine Eigenschaft von Räumen, die unter anderem Beweisführungen erleichtern kann. Oft kann man für Sätze über solche Räume auf Beweistechniken wie die Transfinite Induktion verzichten. Räume mit dieser Eigenschaft sind in gewisser Weise beherrschbar oder klein, d.h. nicht uferlos groß, da sie noch mit abzählbaren Methoden behandelt werden können. So kann man beispielsweise in einem separablen Hilbertraum stets abzählbare Orthonormalbasen finden und damit jedes Element des Raums in eine Reihe, d.h. abzählbare Summe, entwickeln.

Definition

Ein topologischer Raum heißt separabel, wenn es eine abzählbare Teilmenge gibt, die in diesem Raum dicht liegt.

Kriterien für separable Räume

• Ein topologischer Raum mit abzählbarer Basis (zweites Abzählbarkeitsaxiom) ist separabel. Man erhält die abzählbare dichte Teilmenge, indem man aus jeder Menge in der Basis einen Punkt auswählt.
• Jeder kompakte, metrisierbare Raum ist separabel. Genauer gilt, dass für metrisierbare Räume die drei Eigenschaften zweitabzählbar, lindelöf und separabel zu sein äquivalent sind. Kompaktheit ist ein Spezialfall der Lindelöf-Eigenschaft, sodass sich die erstgenannte Aussage aus dieser Äquivalenz als Folgerung ergibt.
• Ein topologischer Vektorraum (über R oder C) ist genau dann separabel, wenn es ein abzählbare Teilmenge gibt, sodass der davon erzeugte Untervektorraum dicht liegt.

Beispiele

Beispiele für separable Räume sind etwa:

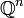• Die Räume $\mathbb{R}^n$ sind für $n\in\mathbb{N}$ separabel, da $\mathbb{Q}^n$ abzählbar ist und dicht in $\mathbb{R}^n$ liegt.
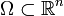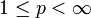• Die Räume L^p(Ω) mit einer beschränkten, offenen Teilmenge $\Omega\subset\mathbb{R}^n$ und $1\leq p<\infty$ sind separabel.
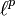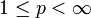• Die Folgenräume $\ell^p$ für $1\leq p<\infty$ sind separabel.
• Die Räume C^k(Ω) sind für natürliches k separabel. Dabei bezeichnet Ω eine offene Teilmenge des $\mathbb{R}^n$.

Gegenbeispiele

• Der Raum der beschränkten Folgen 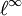$\ell^{\infty}$ ist nicht-separabel.
• Der Raum der fast-periodischen Funktionen ist ein Beispiel eines nicht-separablen Hilbertraums (Der Verweis liefert auch eine genaue Definition dieses Raumes).

Permanenzeigenschaften

• Bilder von separablen Räumen unter stetigen Funktionen sind wieder separabel. Als dichte Teilmenge im Bild dient einfach das Bild der dichten Teilmenge im Definitionsbereich.
• Unterräume separabler Räume sind im Allgemeinen nicht wieder separabel, beispielsweise enthält der separable Niemytzki-Raum einen nicht-separablen Unterraum. Es gilt aber, dass Unterräume separabler, metrischer Räume wieder separabel sind. Dies folgt aus oben genannter Äquivalenz von Separabilität und Zweitabzählbarkeit, denn letztere überträgt sich offensichtlich auf Teilräume.
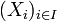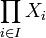• Ist $(X_i)_{i\in I}$ eine Familie separabler Räume und ist die Mächtigkeit von I höchstens gleich der Mächtigkeit des Kontinuums $\mathbb R$, so ist $\prod_{i\in I}X_i$ mit der Produkttopologie ebenfalls separabel. Um dieses erstaunliche Resultat einzusehen, genügt es die Separabilität von 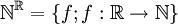${\mathbb N}^{\mathbb R} = \{f; f: {\mathbb R}\rightarrow {\mathbb N}\}$ zu beweisen. Dazu überlegt man sich leicht, dass die abzählbare Menge der endlichen Summen von Funktionen aus $\{n\cdot\chi_{[a,b]}; n\in{\mathbb N}, a,b\in {\mathbb Q}\}$ dicht liegt, wobei χ_[a,b] die charakteristische Funktion des Intervalls [a,b] ist.