Skalenvorteil

Dieser Artikel wurde auf der Koordinationsseite des WiwiWiki-Projekts gelistet um die Bearbeitung effektiver gestalten zu können. Bitte beteilige dich an der Diskussion.

Als Skaleneffekt (Skalenertrag, Größenkostenersparnis, Economies of Scale) definiert man in der Produktionstheorie der Betriebswirtschaftslehre und in der Mikroökonomie die Abhängigkeit der Produktionsmenge von der Menge der eingesetzten Produktionsfaktoren. Der (marginale) Skalenertrag entspricht der Steigung der Niveau-Produktionsfunktion. Er zeigt an, um welchen Betrag sich die Produktionsmenge verändert, wenn der Einsatz aller Produktionsfaktoren (marginal) um einen bestimmten Faktor erhöht wird. Dagegen spricht man von Grenzproduktivität (Grenzertrag) bei partieller Faktorvariation, wenn also nur ein Faktor mengenmäßig marginal verändert wird. Skaleneffekte sind auch abzugrenzen von den Verbund- und Dichtevorteilen.

Arten von Skaleneffekten

Man spricht von konstanten Skaleneffekten, wenn eine Steigerung der Einsatzfaktoren x₁,x₂,.. um einen gegebenen Faktor eine Steigerung der Produktionsmenge um den gleichen Faktor zur Folge hat (Skalenelastizität gleich 1), wenn also für die Produktionsfunktion f gilt:

$f(a\cdot x_1,a\cdot x_2,\dots)=a\cdot f(x_1,x_2,\dots)$

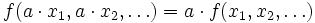
Ein solches Ergebnis ist etwa zu erwarten, wenn eine bestimmte Produktionstechnik in größerem Umfange angewandt wird. Im selben Maße, wie dann die Einsatzmengen der Einsatzfaktoren zunehmen, nimmt auch die Ausbringungsmenge des Endprodukts zu.

Von positiven Skaleneffekten (oder steigenden Skalenerträgen) spricht man, wenn die Produktionsmenge stärker steigt, als die eingesetzten Faktoren (Skalenelastizität größer 1):

$f(a\cdot x_1,a\cdot x_2,\dots)>a\cdot f(x_1,x_2,\dots)$

Für die unternehmerische Praxis interessant ist vor allem der Fall der positiven Skaleneffekte, wobei mit der Produktionsmenge die Grenzkosten sinken: Bei relativ niedrigen Produktionsmengen sind sowohl die Stückkosten eines einzelnen produzierten Exemplars bzw. einer Produktionseinheit, als auch die Grenzkosten (also die Kosten der letzten hergestellten Einheit) relativ hoch. Beide sinken mit steigender Produktionsmenge. Mathematisch ausgedrückt:

$\frac{\partial c'}{\partial q} < 0$

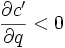
Hierbei stehen c' für die Grenzkosten und q für die erstellte Menge.

Positive Skaleneffekte, also sinkende Grenzkosten, sind die ökonomische Erklärung für die Massenproduktion.

Sie treten aber auch bei der Erstellung vieler Güter der Netzindustrien wie Öffentlicher Personennahverkehr oder Elektrizität auf. In Wirtschaftszweigen mit unbegrenzt steigenden Skaleneffekten führt die (nur in der Theorie anzutreffende) vollständige Konkurrenz dazu, dass kein Produktionsbetrieb mehr seine Herstellkosten decken kann (was auch rein mathematisch beweisbar ist). Daher herrscht in solchen Wirtschaftszweigen vielfach ein (meist staatliches) Monopol.

Negative Skaleneffekte (oder fallende Skalenerträge) (Skalenelastizität kleiner 1) kommen beispielsweise in der landwirtschaftlichen Produktion vor, wenn mit steigendem Einsatz der Produktionsfaktoren wie Arbeit und Düngemittel keine Ertragssteigerung um den gleichen Faktor mehr möglich ist.

Abb. 1: negative Skaleneffekte

Abb 2: konstante Skaleneffekte

Abb. 3: positive Skaleneffekte

Ursachen für positive Skaleneffekte

Positive Skaleneffekte lassen sich auf Einsparungen bei der Massenproduktion zurückführen:

• Nutzung nicht-menschlicher oder nicht-tierischer Arbeitskräfte: Einsatz von Wind und Wasserkraft, Dampfmaschinen sowie Verbrennungs- und Elektromotoren.
• Vorteile aus der Arbeitsteilung, bei der komplexe Abläufe in einfache, leicht zu wiederholende Tätigkeiten zerlegt werden
• Sinkende Durchschnittskosten (Fixkostenanteil an Gesamtkosten sinkt anteilig)
• Einsparungen durch die Verwendung größerer Produktionsmittel, wie z. B. größere Öfen, Tanks und Rohre (Doppelter Rohrdurchmesser kostet nur doppelt soviel Material, hat aber den vierfachen Querschnitt und damit auch die vierfache Kapazität.)
• Größere Mengen verhalten sich statistisch gleichmäßiger und sind daher besser planbar
• Rationalisierungen durch den Einsatz automatisierter Produktionsmittel (Industrieroboter)
• Verwendung normierter Teile und zentralisierte Reservehaltung
• Verbesserte Losgrößenabstimmung bei aufeinander folgenden Dispositionsstufen
• Lernkurveneffekte (hierbei handelt es sich streng genommen nicht um einen Skaleneffekt, da dieser von der Konstanz der Produktionstechnologie ausgeht, während diese beim Lernkurveneffekt typischerweise Veränderungen erfährt)
• Konsolidierung von Betriebsstandorten

Folgen

Positive Skaleneffekte können in Verbindung mit anderen Faktoren ein "natürliches Monopol" begründen. Sie werden auch als Grund für Unternehmenskonzentrationen genannt. Bei positiven Skaleneffekten kann eine Firma mit einem Kapitaleinsatz von 2 Mio. € mehr produzieren als zwei Firmen mit einem Kapitaleinsatz von jeweils 1 Mio. €. Im Wettbewerb setzt sich also die große Firma gegen die beiden kleinen durch. Schreibt man diese Tendenz fort, bleiben in den jeweiligen Wirtschaftszweigen immer weniger, immer größere Firmen übrig, wodurch der Wettbewerb innerhalb der Branchen abgeschwächt wird. Da Wettbewerb aber eine wichtige Voraussetzung für die Effizienz von Märkten ist, kann so durch steigende Skalenerträge Marktversagen begründet werden.

Als Grund für Unternehmenszusammenschlüsse oder Kooperationen sind sie allerdings umstritten, da positive Skaleneffekte eine Produktionsstätte bedingen. Dies wäre nur denkbar bei folgender Spezialisierung der Einzelunternehmen (statt in zwei Unternehmen jeweils zwei Produkte zu produzieren, wird jeweils nur ein Produkt pro Produktionsstätte produziert).

Abgrenzung der Economies of Density

Von den Economies of Scale werden die Economies of Density (Dichtevorteil) deutlich abgegrenzt. Während die Economies of Scale sowohl auf eine Skalenelastizität größer eins (Fixkostendegression), als auch auf eine Betriebsgrößenvariation zurückzuführen sein kann, beschreibt letztere kurzfristige, zeitlich begrenzte, intensitätsmäßige, kombiniert zeitlich-intensitätsmäßige oder quantitative Anpassungen.^[1]

Demgegenüber sind die Economies of Density lediglich von der Fixkostendegression abhängig, da eine konstante Betriebsgröße vorausgesetzt wird.

Weblinks

• Online-Skript von Prof. Dr. Wilhelm Lorenz

Fußnoten

1. ↑ http://www.gut-berlin.de/uploads/media/Skript_Gueterwirtschaft_1106.pdf

Dieser Text basiert ganz oder teilweise auf dem Mikroökonomie-Glossar von Professor Wilhelm Lorenz und ist unter GNU-FDL lizenziert.