- Stochastischer Kern
-
In der Wahrscheinlichkeitstheorie beschreiben Übergangswahrscheinlichkeiten die Wahrscheinlichkeiten, vom Zustand i (in einer Menge Ω) zu einem aktuellen Beobachtungszeitpunkt in bestimmte andere Zustände j (in einer Menge Ω') überzugehen. Sie finden in der Bioinformatik eine breite Anwendung bei der Modellbildung unter Zuhilfenahme von Markow- und Hidden-Markow-Modellen. In der Quantenphysik werden oft Übergangswahrscheinlichkeiten zwischen quantenmechanischen Zuständen untersucht.
Diskreter Fall
Im diskreten Fall, wo Ω und Ω' endliche oder abzählbare Mengen sind, genügt es die Wahrscheinlichkeiten πi,j anzugeben, mit denen man vom Zustand i in den Zustand j gelangt. Diese Wahrscheinlichkeiten bilden eine Matrix
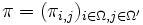 , die die Eigenschaft hat, dass alle Elemente zwischen 0 und 1 liegen und dass die Zeilensummen
, die die Eigenschaft hat, dass alle Elemente zwischen 0 und 1 liegen und dass die Zeilensummen 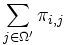 den Wert 1 haben. Eine solche Matrix wird als stochastische Matrix bezeichnet. Sie ordnet jeder Wahrscheinlichkeitsverteilung auf Ω mit einer Zähldichte
den Wert 1 haben. Eine solche Matrix wird als stochastische Matrix bezeichnet. Sie ordnet jeder Wahrscheinlichkeitsverteilung auf Ω mit einer Zähldichte 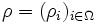 eine Zähldichte
eine Zähldichte 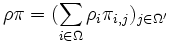 in Ω' zu.
in Ω' zu.Bemerkung: Bei manchen Definitionen werden Zeilen und Spalten der Matrix umgekehrt verwendet.
Allgemeiner Fall
Im allgemeinen Fall gibt man die Wahrscheinlichkeiten π(x;A) an, mit denen man von einem Zustand x zu einem beliebigen Ereignis A gelangt. Dazu seien
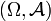 und
und 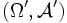 Messräume. Eine Abbildung
Messräume. Eine Abbildung ![\pi : \Omega \times \mathcal A' \to [0,1]](/pictures/dewiki/56/8a1d18af8fb28a5baae70f8164fe02ff.png) heißt stochastischer Kern oder Markow-Kern von
heißt stochastischer Kern oder Markow-Kern von 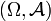 nach
nach 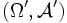 , wenn gilt:
, wenn gilt:- Für jedes
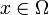 ist
ist 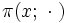 ein Wahrscheinlichkeitsmaß auf
ein Wahrscheinlichkeitsmaß auf 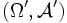 .
. - Für jedes
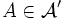 ist
ist 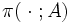 eine
eine  -messbare Funktion.
-messbare Funktion.
Jedem Wahrscheinlichkeitsmaß P auf
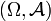 ordnet π durch die Zuordnung
ordnet π durch die Zuordnung 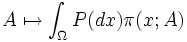 ein Wahrscheinlichkeitsmaß auf
ein Wahrscheinlichkeitsmaß auf 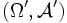 zu.
zu.Bemerkung: Bei manchen Definitionen werden die Argumente von π in umgekehrter Reihenfolge geschrieben, π(A;x) oder auch π(A | x), in Anlehnung an bedingte Wahrscheinlichkeiten.
- Für jedes
Wikimedia Foundation.
