- Bedingte Erwartung
-
Bedingte Erwartungswerte und bedingte Wahrscheinlichkeiten bezüglich einer Teil-σ-Algebra stellen eine Verallgemeinerung von bedingten Wahrscheinlichkeiten dar. Sie werden unter anderem bei der Formulierung von Martingalen verwendet.
Inhaltsverzeichnis
Einleitung
Ein Beispiel
Wenn zwei unabhängige standardnormalverteilte Zufallsvariablen X und Y gegeben sind, kann man, ohne lange zu überlegen, den bedingten Erwartungswert der Zufallsvariable Z = 2X + Y − 3 angeben, d. h. den Wert, den man im Mittel für den Ausdruck 2X + Y − 3 erwartet, wenn man X kennt:
- E(Z | X) = 2X − 3
Diese Gleichung wirft jedoch mehrere technische Fragen auf, die generell eine etwas sorgfältigere Vorgehensweise bei der Definition erforderlich machen:
- Der Ausdruck E(Z | X) auf der linken Seite ergibt nur Sinn, wenn man X als eine Zufallsvariable auffasst. Man kann z. B. nicht für X den Wert 5 einsetzen und schreiben E(Z | 5) = 7.
- Wenn man X als eine Zufallsvariable auffasst, dann ist notwendigerweise der Ausdruck 2X − 3 auf der rechten Seite, der eine Funktion von X ist, ebenfalls eine Zufallsvariable. Der bedingte Erwartungswert ist somit eine Zufallsvariable.
- Wenn man eine Zufallsvariable X' durch X' = 2X definiert, gilt E(Z | X') = E(X' + Y − 3 | X') = X' − 3 = 2X − 3. Also hängt der bedingte Erwartungswert von Z nicht davon ab, welche Werte die Zufallsvariable in der Bedingung (X bzw. X') annimmt, sondern nur davon, welche Informationen die Werte implizieren. Diese Informationen können durch die von der Zufallsvariable erzeugte Teil-σ-Algebra beschrieben werden, die für X und X' übereinstimmt und die daher für eine allgemeine Definition verwendet werden kann.
- Die Gleichung E(Z | X) = 2X − 3 geht davon aus, dass Y für jeden einzelnen Wert von X standardnormalverteilt ist. Tatsächlich könnte man aber auch annehmen, dass Y im Fall X = 0 konstant 0 ist und nur in den übrigen Fällen standardnormalverteilt ist: Da das Ereignis X = 0 die Wahrscheinlichkeit 0 hat, wären X und Y insgesamt immer noch unabhängig und standardnormalverteilt. Man erhielte aber E(Z | X) = 2X − 3 nur noch, wenn X nicht 0 ist, und sonst E(Z | X) = 0. Das zeigt, dass der bedingte Erwartungswert nicht eindeutig festgelegt ist, und dass es, wenn überhaupt, nur sinnvoll ist, den bedingten Erwartungswert für alle Werte von X simultan zu definieren, da man ihn für einzelne Werte beliebig abwandeln kann.
Herleitung aus bedingten Wahrscheinlichkeiten
In einem Wahrscheinlichkeitsraum
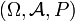 gibt die bedingte Wahrscheinlichkeit P(A | B) an, wie wahrscheinlich das Ereignis A ist, wenn man Information über das Eintreten von B erhalten hat. Allgemeiner kann man nach der Wahrscheinlichkeit
gibt die bedingte Wahrscheinlichkeit P(A | B) an, wie wahrscheinlich das Ereignis A ist, wenn man Information über das Eintreten von B erhalten hat. Allgemeiner kann man nach der Wahrscheinlichkeit 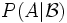 fragen, die angibt, wie wahrscheinlich A ist, wenn man Information über das Eintreten bzw. Nichteintreten einer Menge
fragen, die angibt, wie wahrscheinlich A ist, wenn man Information über das Eintreten bzw. Nichteintreten einer Menge  von Ereignissen erhalten hat. Man kann dabei annehmen, dass
von Ereignissen erhalten hat. Man kann dabei annehmen, dass  eine σ-Algebra ist, denn die Information über bestimmte Ereignisse impliziert immer auch Information über die von den Ereignissen erzeugte σ-Algebra. Wenn die Information beispielsweise darin besteht, dass man den Wert von Zufallsvariablen
eine σ-Algebra ist, denn die Information über bestimmte Ereignisse impliziert immer auch Information über die von den Ereignissen erzeugte σ-Algebra. Wenn die Information beispielsweise darin besteht, dass man den Wert von Zufallsvariablen 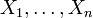 kennt, dann weiß man, unabhängig vom jeweiligen Wert, über alle Ereignisse der Form
kennt, dann weiß man, unabhängig vom jeweiligen Wert, über alle Ereignisse der Form 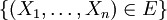 Bescheid, d. h.
Bescheid, d. h.  ist in diesem Fall die von den Zufallsvariablen erzeugte σ-Algebra
ist in diesem Fall die von den Zufallsvariablen erzeugte σ-Algebra 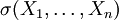 . Die Wahrscheinlichkeit
. Die Wahrscheinlichkeit 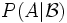 hängt dann davon ab, welchen Wert
hängt dann davon ab, welchen Wert 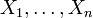 annehmen, oder allgemein, welche Ereignisse von
annehmen, oder allgemein, welche Ereignisse von  eingetreten sind und welche nicht eingetreten sind, d. h.
eingetreten sind und welche nicht eingetreten sind, d. h. 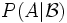 ist eine Funktion von
ist eine Funktion von 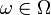 , die messbar bezüglich
, die messbar bezüglich  ist. In Analogie zur Fallunterscheidungsformel für die totale Wahrscheinlichkeit ergibt sich für jedes
ist. In Analogie zur Fallunterscheidungsformel für die totale Wahrscheinlichkeit ergibt sich für jedes 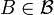
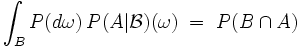 ,
,
was sich auch schreiben lässt als
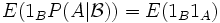 , wobei 1A, 1B die Indikatorfunktion von A bzw. B ist.
, wobei 1A, 1B die Indikatorfunktion von A bzw. B ist.Dieser Ansatz stellt eine Möglichkeit dar, den Begriff der bedingten Wahrscheinlichkeit P(A | B) zu verallgemeinern. Eine andere Möglichkeit ist, dass man den zur bedingten Wahrscheinlichkeitsverteilung
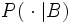 gehörenden Erwartungswert einer Zufallsvariable
gehörenden Erwartungswert einer Zufallsvariable 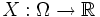 betrachtet. Beide Ansätze werden in der nachfolgenden Definition kombiniert.
betrachtet. Beide Ansätze werden in der nachfolgenden Definition kombiniert.Definition
X sei eine reelle Zufallsvariable in einem Wahrscheinlichkeitsraum
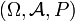 und
und 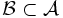 sei eine Teil-σ-Algebra.
sei eine Teil-σ-Algebra.Eine reelle Zufallsvariable Y heißt bedingter Erwartungswert von X bezüglich
 , geschrieben
, geschrieben 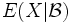 , wenn folgende Bedingungen erfüllt sind:
, wenn folgende Bedingungen erfüllt sind:- Y ist messbar bezüglich
 und
und - für alle
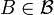 , für die E(1BY) definiert ist (endlich oder unendlich), gilt:
, für die E(1BY) definiert ist (endlich oder unendlich), gilt:
- E(1BY) = E(1BX).
Zwei verschiedene bedingte Erwartungswerte von X bezüglich
 unterscheiden sich höchstens auf einer Nullmenge in
unterscheiden sich höchstens auf einer Nullmenge in  , wodurch sich die einheitliche Schreibweise
, wodurch sich die einheitliche Schreibweise 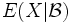 rechtfertigen lässt.
rechtfertigen lässt.Ist
 die von Zufallsvariablen
die von Zufallsvariablen 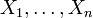 erzeugte σ-Algebra
erzeugte σ-Algebra 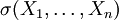 , so schreibt man auch
, so schreibt man auch 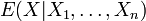 .
.Die bedingte Wahrscheinlichkeit eines Ereignisses
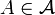 bezüglich
bezüglich  ist definiert als die Zufallsvariable
ist definiert als die Zufallsvariable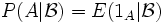 .
.
Da die bedingten Wahrscheinlichkeiten
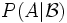 verschiedener Ereignisse
verschiedener Ereignisse 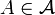 somit ohne Bezug zueinander definiert sind und nicht eindeutig festgelegt sind, muss
somit ohne Bezug zueinander definiert sind und nicht eindeutig festgelegt sind, muss 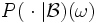 im allgemeinen kein Wahrscheinlichkeitsmaß sein. Wenn dies jedoch der Fall ist, d. h. wenn man die bedingten Wahrscheinlichkeiten
im allgemeinen kein Wahrscheinlichkeitsmaß sein. Wenn dies jedoch der Fall ist, d. h. wenn man die bedingten Wahrscheinlichkeiten 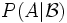 ,
, 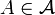 zu einem stochastischen Kern π von
zu einem stochastischen Kern π von 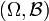 nach
nach 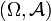 zusammenfassen kann,
zusammenfassen kann,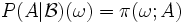 für alle
für alle 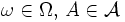 ,
,
spricht man von regulärer bedingter Wahrscheinlichkeit.
Faktorisierung: Der bedingte Erwartungswert
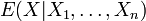 , der als eine Funktion von ω definiert ist, lässt sich auch als eine Funktion von
, der als eine Funktion von ω definiert ist, lässt sich auch als eine Funktion von 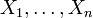 darstellen: Es gibt eine messbare Funktion f, so dass
darstellen: Es gibt eine messbare Funktion f, so dass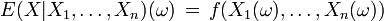 für alle
für alle 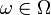 .
.
Existenz: Die allgemeine Existenz bedingter Erwartungswerte für integrierbare Zufallsvariablen (Zufallsvariablen, die einen endlichen Erwartungswert besitzen) lässt sich mit dem Satz von Radon-Nikodym zeigen. In der hier angegebenen Definition existiert der bedingte Erwartungswert
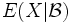 genau dann, wenn es eine Menge
genau dann, wenn es eine Menge 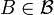 gibt, so dass 1BX und
gibt, so dass 1BX und 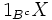 quasiintegrierbar sind, und es gilt dann
quasiintegrierbar sind, und es gilt dann 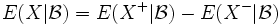 fast überall. (Man könnte auch letzteren Ausdruck für die Definition verwenden, um Fälle wie E(X | | X | ) = 0 für eine Cauchy-verteilte Zufallsvariable zu erfassen, würde dann aber inkonsistente Erwartungswerte erhalten.)
fast überall. (Man könnte auch letzteren Ausdruck für die Definition verwenden, um Fälle wie E(X | | X | ) = 0 für eine Cauchy-verteilte Zufallsvariable zu erfassen, würde dann aber inkonsistente Erwartungswerte erhalten.)Reguläre bedingte Wahrscheinlichkeiten, auch in faktorisierter Form, existieren in polnischen Räumen mit der Borel-σ-Algebra, allgemeiner gilt: Ist Z eine beliebige Zufallsvariable mit Werten in einem polnischen Raum, so existiert eine Version der Verteilung
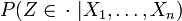 in der Form eines stochastischen Kerns π:
in der Form eines stochastischen Kerns π: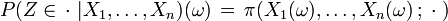 für alle
für alle 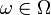
Beispiele
Einfache σ-Algebren: Ist
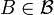 mit P(B) > 0, und besitzt B außer sich selbst und der leeren Menge keine Teilmengen in
mit P(B) > 0, und besitzt B außer sich selbst und der leeren Menge keine Teilmengen in  , so stimmt der Wert von
, so stimmt der Wert von 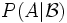 auf B mit der herkömmlichen bedingten Wahrscheinlichkeit überein:
auf B mit der herkömmlichen bedingten Wahrscheinlichkeit überein: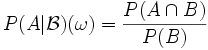 für alle
für alle 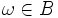
Rechnen mit Dichten: Ist
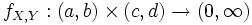 eine beschränkte Dichte der gemeinsamen Verteilung von Zufallsvariablen X,Y, so ist
eine beschränkte Dichte der gemeinsamen Verteilung von Zufallsvariablen X,Y, so istdie Dichte einer regulären bedingten Verteilung
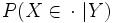 in der faktorisierten Form.
in der faktorisierten Form.Rechenregeln
Die Gleichungen sind, soweit nichts anderes angegeben ist, jeweils so zu verstehen, dass die linke Seite genau dann existiert (im Sinne der obigen Definition), wenn die rechte Seite existiert.
- Für die triviale σ-Algebra
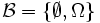 ergeben sich einfache Erwartungswerte und Wahrscheinlichkeiten:
ergeben sich einfache Erwartungswerte und Wahrscheinlichkeiten:
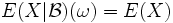 für alle
für alle 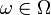
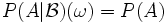 für alle
für alle 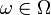
- Ist X unabhängig von
 , so gilt
, so gilt 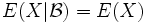 fast überall.
fast überall.
- Ist
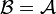 oder X messbar bezüglich
oder X messbar bezüglich  , so gilt
, so gilt 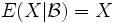 fast überall.
fast überall.
- Turmeigenschaft: Für Teil-σ-Algebren
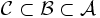 gilt
gilt 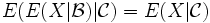 und
und 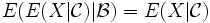 fast überall.
fast überall.
- Es gilt
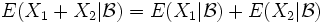 fast überall, wenn X1 oder X2 einen endlichen Erwartungswert besitzt.
fast überall, wenn X1 oder X2 einen endlichen Erwartungswert besitzt.
- Es gilt
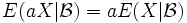 fast überall für reelle Zahlen
fast überall für reelle Zahlen 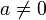 .
.
- Monotonie: Aus
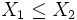 folgt
folgt  fast überall, wenn die bedingten Erwartungswerte existieren.
fast überall, wenn die bedingten Erwartungswerte existieren.
- Monotone Konvergenz: Aus
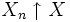 folgt
folgt 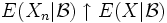 fast überall, wenn die bedingten Erwartungswerte existieren und
fast überall, wenn die bedingten Erwartungswerte existieren und 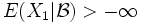 fast überall.
fast überall.
- Jensensche Ungleichung: Ist
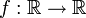 eine konvexe Funktion, so gilt
eine konvexe Funktion, so gilt 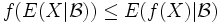 fast überall, wenn die bedingten Erwartungswerte existieren.
fast überall, wenn die bedingten Erwartungswerte existieren.
- Ist Y messbar bezüglich
 , so gilt
, so gilt 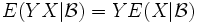 fast überall, wenn die bedingten Erwartungswerte existieren. Insbesondere ist
fast überall, wenn die bedingten Erwartungswerte existieren. Insbesondere ist 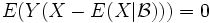 fast überall, d. h. der bedingte Erwartungswert
fast überall, d. h. der bedingte Erwartungswert 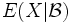 ist im Sinne des Skalarprodukts von L2(P) die orthogonale Projektion von X auf den Raum der
ist im Sinne des Skalarprodukts von L2(P) die orthogonale Projektion von X auf den Raum der  -messbaren Funktionen.
-messbaren Funktionen.
- Ist Y messbar bezüglich
 und ist für jedes y im Bild von Y ein Ereignis Ay gegeben, so dass
und ist für jedes y im Bild von Y ein Ereignis Ay gegeben, so dass 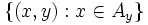 eine messbare Menge ist, dann gilt
eine messbare Menge ist, dann gilt 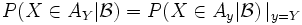 fast überall, sofern auf der rechten Seite eine reguläre bedingte Verteilung
fast überall, sofern auf der rechten Seite eine reguläre bedingte Verteilung 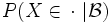 verwendet wird.
verwendet wird.
Wikimedia Foundation.