Subtrahierer

Der Subtrahierer ist eine elektronische Schaltung der Analogtechnik zur Messung von elektrischen Potentialdifferenzen.

In der Praxis werden Subtrahierer aus Operationsverstärkern, gegengekoppelten Differenzverstärkern oder mit geschalteten Kondensatoren (Switched-Capacitor-Technik) realisiert.

Eingangswiderstand und Güte

Beim Subtrahierer ist der Eingangswiderstand von besonderem Interesse, da es bei Messungen der Potentialdifferenz U_diff mit

U_D = ϕ₂ − ϕ₁

wichtig ist, die Potenzialdifferenz möglichst unabhängig von der der Differenz überlagerten Gleichtaktspannung U_Gl mit

$U_{Gl} = \frac{\phi_1 + \phi_2}{2}$

zu messen, da die Gleichtaktspannung in der Praxis häufig um den Faktor 10⁴ oder mehr größer sein kann.

Die Güte G der Gleichtaktunterdrückung (engl.: CMRR - common mode rejection ratio) ist durch die Gleichung

$G = \frac{A_D}{A_{Gl}} = \frac{ \frac{U_a}{U_D} }{ \frac{U_D}{U_{Gl}} }$

beschrieben. Der Wert der Güte des Subtrahierers muss dabei wesentlich größer sein als das Verhältnis von der minimalen zu messenden Potenzialdifferenz zur maximalen Gleichtaktspannung, um einen korrekten Wert zu liefern.

Weitere Probleme können sich zudem ergeben, wenn die Gleichtaktspannung eigene Frequenzen aufweist, da hier auch das Frequenz- und Laufzeitverhalten – sowie die veränderte Verstärkung – der Schaltung berücksichtigt werden muss.

Aufbau mit Operationsverstärker

Subtrahierer aus Inverter und Addierer

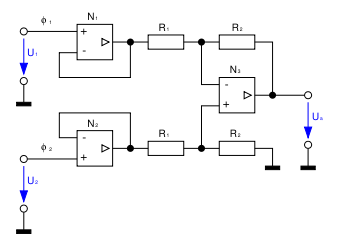
Eine Subtraktion lässt sich auf eine Addition zurückführen, indem man das zu subtrahierende Signal invertiert und anschließend die beiden Signale addiert. Bei der im Bild gezeigten Schaltung wird die Eingangsspannung U₂ am Operationsverstärker N₁ invertiert. Der Operationsverstärker N₂ bildet eine Additionsschaltung und addiert die Spannung U₁ mit dem invertiertem Signal. Dadurch ergibt sich für die Ausgangsspannung der Zusammenhang

$U_a = A_1 \, U_2 - A_2 \, U_1$

wobei A₁ und A₂ die Verstärkungen der jeweiligen Schaltungen mit N₁ bzw. N₂ darstellen. Eine reine Differenzverstärkung ergibt sich, wenn man die beiden Verstärkungen gleich groß wie die geforderte Differenzverstärkung wählt

$A_1 = A_2 = A_{diff} \to U_a = A_{diff} \,\left( U_2 - U_1 \right)$

Zur Berechnung der Gleichtaktverstärkung (d. h. die Abweichung von der idealerweise reinen Differenzverstärkung) ist in dieser Schaltung gegeben durch

$G = \frac{A_D}{A_{Gl}}$

Durch Einsetzen von

$U_2 = U_{Gl} + \frac{1}{2} \, U_D$

und

$U_1 = U_{Gl} - \frac{1}{2} \, U_D$

erhält man

$U_a = A_1 \, U_2 - A_2 \, U_1$

$U_a = A_1 \, \left(U_{Gl} + \frac{1}{2} \, U_D \right) \ - A_2 \, \left(U_{Gl} - \frac{1}{2} \, U_D \right)$

$U_a = \left( A_1 - A_2 \right) \, U_{Gl} + \frac{1}{2} \, \left( A_1 + A_2 \right) \, U_D$

$U_a = A_{Gl} \, U_{Gl} + A_D \, U_D$

Hierbei ist U_Gl die Gleichtaktspannung, A_Gl die Gleichtaktverstärkung, U_D die Differenzspannung und A_D die Differenzverstärkung.

Die Gleichtaktunterdrückung ergibt sich folglich aus

$G = \frac{A_D}{A_{Gl}} = \frac{A_2 + A_1}{2\,\left( A_2 - A_1 \right) }$

Um eine maximale Gleichtaktunterdrückung zu erreichen, muss also

A₁ = A₂ = A_diff

gelten. Dies wird als Koeffizientenbedingung bezeichnet. In diesem Fall gilt weiter:

$A_1 = A - \frac{\Delta A}{2}$

$A_2 = A + \frac{\Delta A}{2}$

Durch Einsetzen erhält man

$G = \frac{A_2 + A_1}{2\,\left( A_2 - A_1 \right) }$

$G = \frac{A + \frac{\Delta A}{2} + A - \frac{\Delta A}{2}}{2\,\left( A + \frac{\Delta A}{2} - (A - \frac{\Delta A}{2}) \right) }$

$G = \frac{A}{\Delta A}$

Dies bedeutet, dass die Gleichtaktunterdrückung gleich dem Kehrwert der relativen Paarungstoleranz der beiden Verstärkungen ist.

Subtrahierverstärker

Subtrahierer mit einem Operationsverstärker

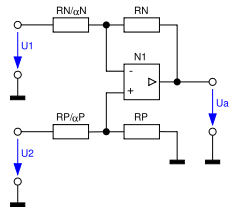
Ein Subtrahierer kann auch vereinfacht mit nur einem Operationsverstärker aufgebaut werden. Dazu schließt man das zu subtrahierende Signal an den jeweils inversen Anschluss des Operationsverstärkers. Hierbei nutzt man aus, dass der Operationsverstärker nur die Differenzspannung zwischen dessen N- und P-Eingang verstärkt.

Funktionsweise

Über den Überlagerungssatz gilt für die nebenstehende Schaltung die Gleichung

$U_a = k_1 \, U_1 + k_2 \, U_2$

Mit U₂ = 0 arbeitet der Subtrahierverstärker als Umkehrverstärker:

$U_a = - \alpha_N \, U_1 \to k_1 = - \alpha_N$

Mit U₁ = 0 arbeitet die Schaltung als Elektrometerverstärker (d. h., der Ausgang wird nicht invertiert) mit einem vorgeschalteten Spannungsteiler. Das Potenzial ϕ_P am P-Anschluss des Operationsverstärkers N₁ ergibt sich aus

$\phi_P = U_2 \, \frac{R_P}{R_P + \frac{R_P}{\alpha_P}}$

und wird um den Faktor 1 + α_N verstärkt. Somit gilt:

$U_a = \frac{\alpha_P}{1 + \alpha_P} \, \left( 1 + \alpha_N \right) \, U_2$

Gleiches Widerstandsverhältnis

Für den Fall, dass die beiden Widerstandsverhältnisse gleich sind, also:

$\frac{\frac{R_N}{\alpha_N}}{R_N} = \frac{\frac{R_P}{\alpha_P}}{R_P}$

und damit

α = α_N = α_P

gilt, folgt durch Einsetzen in die obenstehende Gleichung:

$U_a = \alpha U_2 \to k_2 = \alpha$

Für die Ausgangsspannung folgt schließlich:

$U_a = \alpha\,\left( U_2 - U_1 \right)$

Ungleiches Widerstandsverhältnis

Für den Fall, dass die beiden Widerstandsverhältnisse nicht gleich sind, gilt:

$U_a = \frac{1 + \alpha_N}{1 + \alpha_P} \, \alpha_P \, U_2 - \alpha_N \, U_1$

Gleichtaktunterdrückung

Zur Berechnung der Gleichtaktunterdrückung verwenden wir wieder obenstehende Gleichungen

$U_2 = U_{Gl} + \frac{1}{2} \, U_D$

und

$U_1 = U_{Gl} - \frac{1}{2} \, U_D$

Durch Einsetzen erhält man

$U_a = \frac{1 + \alpha_N}{1 + \alpha_P} \, \alpha_P \, \left(U_{Gl} + \frac{1}{2} \, U_D \right)\ - \alpha_N \, \left(U_{Gl} - \frac{1}{2} \, U_D \right)$

$U_a = \left(\frac{1 + \alpha_N}{1 + \alpha_P} \, \alpha_P \, - \alpha_N \right)\, U_{Gl} + \left(\frac{1 + \alpha_N}{1 + \alpha_P} \, \alpha_P \, + \alpha_N \right)\, \frac{1}{2}\, U_D$

wo

$A_{Gl} = \frac{1 + \alpha_N}{1 + \alpha_P} \, \alpha_P \, - \alpha_N$

$A_D = \frac{1}{2} \left(\frac{1 + \alpha_N}{1 + \alpha_P} \, \alpha_P \, + \alpha_N \right)$

Die Gleichtaktunterdrückung ergibt sich folglich aus

$U_{Gl} = \frac{A_D}{A_{Gl}} =\frac{1}{2} \, \frac{\left( 1 + \alpha_N \right) \, \alpha_P + \left( 1 + \alpha_P \right) \, \alpha_N}{\left( 1 + \alpha_N \right) \, \alpha_P - \left( 1 + \alpha_P \right) \, \alpha_N}$

Mit der Koeffizientenbedingung

$\alpha_N = \alpha - \frac{\Delta \alpha}{2}$

$\alpha_P = \alpha - \frac{\Delta \alpha}{2}$

folgt eine Vernachlässigung der Terme höherer Ordnung:

$G \approx \left( 1 + \alpha \right) \, \frac{\alpha}{\Delta \alpha}$

Die Gleichtaktunterdrückung ist also invers proportional zur Toleranz der Widerstandsverhältnisse, wenn der Faktor α konstant ist. Sind die beiden Widerstandsverhältnisse gleich, gilt:

$G = \infty$

was jedoch nur mit einem idealen Operationsverstärker erreicht werden kann, der in der Praxis nicht vorkommt. Wird eine möglichst hohe Gleichtaktunterdrückung gefordert, wird etwa R_P so eingestellt, dass die endliche Gleichtaktunterdrückung des Operationsverstärkers möglichst stark kompensiert wird. Zudem ist die Gleichtaktunterdrückung bei einer vorhandenen Widerstandstoleranz mit

$\frac{\Delta \alpha}{\alpha}$

annähernd proportional zur eingestellten Differenzverstärkung:

A_D = α

Mehrfach-Subtrahierer

Mehrfach-Subtrahierer

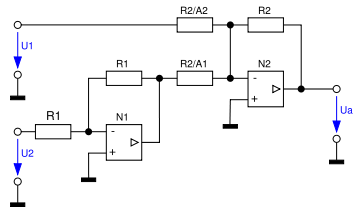
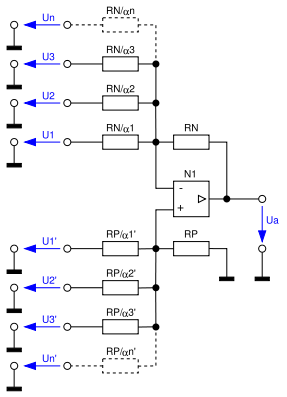
In der nebenstehenden Abbildung ist die Erweiterung des Subtrahierers für eine beliebige Anzahl von Additionen und Subtraktionen dargestellt. Bei dieser Schaltung muss die Koeffizientenbedingung erfüllt sein, damit die korrekte Arbeitsweise der Schaltung gewährleistet ist. Ist dies nach der Vergabe der Koeffizienten nicht der Fall, wird dem fehlenden Koeffizienten die Spannung 0 addiert bzw. subtrahiert – d. h., man berechnet einen zusätzlichen Additions- bzw. Subtraktionseingang mit einem passenden Koeffizienten und legt diesen auf Masse.

Über die Knotenregel erhält man für den N-Eingang:

$\sum^{m}_{i=1} \frac{U_i - \phi_N}{\frac{R_N}{\alpha_i}} + \frac{U_a - \phi_N}{R_N} = 0$

daraus folgt:

$\sum^{m}_{i=1} {\alpha_i \, U_i} - \phi_N \left( \sum^{m}_{i=1} { \alpha_i } + 1 \right) + U_a = 0$

Ebenfalls über die Knotenregel erhält man für den P-Eingang:

$\sum^{n}_{i=1} {\alpha'_i \, U'_i} - \phi_P \left( \sum^{n}_{i=1} { \alpha'_i } + 1 \right) = 0$

Wenn die zusätzlichen Bedingungen

ϕ_N = ϕ_P

und

$\sum^{m}_{i=1} {\alpha_i} = \sum^{n}_{i=1} {\alpha'_i}$

erfüllt sind, folgt durch Subtraktion der beiden Gleichungen die Gleichung

$U_a = \sum^{n}_{i=1} {\alpha'_i \, U'_i} - \sum^{m}_{i=1} {\alpha_i \, U_i}$

Subtrahierer mit hochohmigen Eingängen

Subtrahierer aus Subtrahierverstärker mit Impedanzwandlern

Der Aufbau des Subtrahierers mit hochohmigen Eingängen basiert im Wesentlichen auf dem Subtrahierverstärker, bietet jedoch zusätzliche Spannungsfolger an den Eingängen, um die zu messenden Potenziale nicht mit dem Eingangswiderstand des Subtrahierers zu belasten. Zudem lässt sich eine höhere Gleichtaktunterdrückung erzielen, wenn man die Spannungsverstärkung in die Impedanzwandler verlagert und auf dem Subtrahierer die Verstärkung 1 eingestellt wird.

Für den im Bild gezeigten Subtrahierverstärer mit Impedanzwandlern gilt hierbei die folgende Gleichung:

$U_a = \left( \phi_2 - \phi_1 \right) \, \frac{R_2}{R_1}$

Symmetrischer Elektrometersubtrahierer

Elektrometersubtrahierer

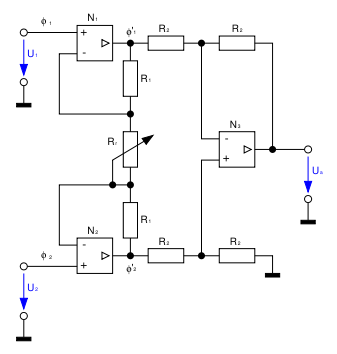
Ein Spezialfall dieses Typs ist der (symmetrische) Elektrometersubtrahierer, bei dem zwischen den beiden Impedanzwandlern ein zusätzlicher Widerstand R_r geschaltet wird. Dieser Schaltungstyp wird allgemein als Instrumentierungsverstärker, Instrumentenverstärker^[1], Instrumentationsverstärker oder engl. Instrumentation Amplifier, kurz InAmp, bezeichnet. Diese Schaltung ist eine besonders präzise Operationsverstärker-Schaltung mit sehr hochohmigen (typ. 1 GΩ) Eingängen, besonders hoher Gleichtaktunterdrückung und geringer Eingangs-Offsetspannung.

Der Widerstand R_r macht die Differenzverstärkung einstellbar. Bei $R_r = \infty$ arbeiten die beiden Operationsverstärker am Eingang als Spannungsfolger, was dem Subtrahierverstärer mit Impedanzwandlern ohne R_r entspricht. Am Widerstand R_r tritt die Potenzialdifferenz ϕ₂ − ϕ₁ auf. Dadurch gilt:

$\phi'_2 - \phi'_1 = \left( \phi_2 - \phi_1 \right) \, \left( 1 + \frac{2\, R_1}{R_r} \right)$

Die Differenz ϕ'₂ − ϕ'₁ wird dabei an den Ausgang übertragen.

Bei einer reinen Gleichtaktaussteuerung gilt

ϕ₁ = ϕ₂ = ϕ'₁ = ϕ'₂ = ϕ_Gl

wodurch die Gleichtaktverstärkung immer den Faktor 1 aufweist. Dadurch ergibt sich für die Gleichtaktunterdrückung der Zusammenhang

$G = \left( 1 + \frac{2 \, R_1}{R_r} \right) \, \frac{2\,\alpha}{\Delta\alpha}$

wobei der Faktor $\frac{2\,\alpha}{\Delta\alpha}$ die relative Paarungstoleranz der Widerstände R₂ darstellt.

siehe Hauptartikel: Instrumentierungsverstärker

Asymmetrischer Elektrometersubtrahierer

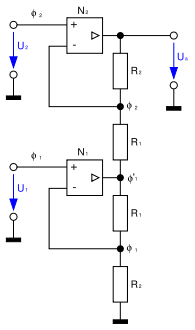
Durch einen asymmetrischen Aufbau des Elektrometersubtrahierers kann der Operationsverstärker am Ausgang entfallen.

Asymmetrischer Elektrometersubtrahierer

Der im ersten Bild gezeigte asymmetrische Elektrometersubtrahierer verstärkt das Eingangssignal mit U₁ am Operationsverstärker N₁ mit der Verstärkung

$1+\frac{R_1}{R_2}$

und das Eingangssignal mit U₂ am Operationsverstärker N₂ mit der Verstärkung

$1+\frac{R_2}{R_1}$.

Zusätzlich addiert sich das in den Flusspunkt induzierte Potenzial ϕ'₁ mit der Gewichtung

$- \frac{R_2}{R_1}$.

Betragsmäßig werden also die beiden Eingangsspannungen um den Faktor

$1+\frac{R_2}{R_1}$

verstärkt. Daher ergibt sich für die Ausgangsspannung

$U_a = \left( \phi_2 - \phi_1 \right) \, \left( 1+\frac{R_2}{R_1} \right)$

---

Wie im zweiten Bild gezeigt, kann durch die Verwendung eines zusätzlichen (regelbaren) Widerstandes R_r zwischen den Potenzialen ϕ₁ und ϕ₂ die Verstärkung der Schaltung eingestellt werden. Für die Ausgangsspannung gilt die Gleichung

$U_a = \left( \phi_2 - \phi_1 \right) \, 2\, \left( 1 + \frac{R_2}{R_1} \right)$

---

Bei Anwendungen, bei denen nur ein hochohmiger Eingang benötigt wird, kann auch die im dritten Bild gezeigte Schaltung verwendet werden. Diese benötigt nur einen einzigen Operationsverstärker. Allerdings ist die Verstärkung von U₂ immer größer als die von U₁, was die Einsatzmöglichkeiten weiter einschränkt, was jedoch beispielsweise bei der Verstärkung und Nullpunktverschiebung von Sensorsignalen keinen Nachteil darstellt. Für die Ausgangsspannung gilt die Gleichung

$U_a = U_2 \, \left( 1 + \frac{R_N}{R_1} + \frac{R_N}{R_2} \right) - U_1 \, \frac{R_N}{R_1}$

Zudem erhält man durch das Weglassen von R₂ ($R_2 = \infty$) einen herkömmlichen Verstärker. Setzt man zudem noch R₁ = R_N so gilt für die Ausgangsspannung der Zusammenhang

$U_a = 2\, U_2 - U_1$

Hochspannungssubtrahierer

Hochspannungssubtrahierer

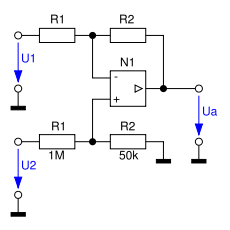
Auch zur Subtraktion von Hochspannungen werden hochohmige Eingänge benötigt. Da jedoch eine hohe Dämpfung erforderlich ist, um die Hochspannung am Eingang auf eine Niederspannung am Ausgang zu reduzieren, wählt man $R_1 \gg R_2$. Dadurch, dass die beiden Widerstände R₁ und damit die Eingänge sehr hochohmig sind, können die Impedanzverstärker am Eingang entfallen. Gleichzeitig wird über den Spannungsteiler, bestehend aus R₁ und R₂ die Spannung so weit heruntergesetzt, dass man keinen Hochspannungs-Operationsverstärker benötigt.

Der in der ersten Abbildung gezeigte Hochspannungssubtrahierer hat den Nachteil, dass das Differenzsignal ebenfalls sehr stark gedämpft wird. Für die Verstärkung in der ersten Schaltung gilt:

$A = \frac{R_2}{R_1} \ll 1$

Um bei kleinen Spannungsdifferenzen dennoch eine möglichst große Aussteuerung zu erreichen, muss daher ein zusätzlicher Verstärker am Ausgang eingesetzt werden, wodurch sich jedoch das Signal-Rausch-Verhältnis verschlechtert.

Um dieses Problem zu umgehen, kann man den Hochspannungssubtrahierer mit einstellbarer Verstärkung einsetzen. Bei dieser Schaltung kann die Dämpfung der hohen Eingangsspannungen und die Verstärkung der Differenzspannung getrennt dimensioniert werden. Die Widerstände R₁ und R₂ bestimmen die Verstärkung, während die Widerstände R₃ nur auf die Gleichtaktaussteuerung wirken. Der in der Abbildung gezeigte Hochspannungssubtrahierer mit einstellbarer Verstärkung entspricht dem INA 148 von Burr Brown und hat die Verstärkung 1 für die Spannungsdifferenz.

Nachteilig am Hochspannungssubtrahierer mit einstellbarer Verstärkung ist jedoch, dass die beiden R₃-Widerstände die Eingangssignale des Operationsverstärkers dämpfen. Dadurch reduziert sich die Schleifenverstärkung und folglich auch die Bandbreite der Schaltung. Zudem wird die Offsetspannung und der Offsetspannungsdrift des Operationsverstärkers verstärkt. Dadurch werden in dieser Schaltung wesentlich bessere Operationsverstärker benötigt. Zudem benötigt man für die beiden R₃-Widerstände Bauteile mit sehr geringer Toleranz. Die Widerstände R₂ und R₃ am nichtinvertierenden Eingang werden nicht zusammengefasst, um eine möglichst geringe Gleichlauftoleranz sicherzustellen.

Aufbau mit Differenzverstärker

Elektrometer-Subtrahierer mit gegengekoppelten Differenzverstärkern

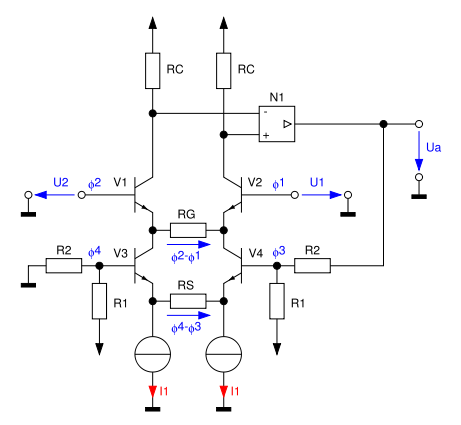
Durch die manuelle Dimensionierung der Stromgegenkopplung kann man die Differenzverstärkung des Differenzverstärkers einstellen. Zudem lässt sich im Differenzverstärker durch den Einsatz einer Konstantstromquelle am Emitter eine hohe Gleichtaktunterdrückung erzielen. Eine solche Schaltung ist in der nebenstehenden Abbildung dargestellt.

Die Transistoren V₁ und V₂ bilden hierbei den eigentlichen Differenzverstärker an den Eingängen der Schaltung und sind über den Widerstand R_G gegengekoppelt. Die Differenz der Kollektorstöme wird an dem Operationsverstärker N₁ in die Ausgangsspannung umgesetzt.

Mit dem zweiten Differenzverstärker – bestehend aus V₃ und V₄ – wird eine gleich große Stromdifferenz gebildet.

$\Delta I_C = \frac{V_2 - V_1}{R_G} = \frac{V_4 - V_3}{R_S}$

Dadurch wird die Stromdifferenz kompensiert, so dass die Kollektorströme von V₁ und V₂ immer denselben Strom wie die Stromquellen (I₁) aufweisen. Erreicht wird dies, indem der Operationsverstärker N₁ an V₄ gegengekoppelt wird.

Hierbei gilt für die Ausgangsspannung U_a:

$U_a = \left( \phi_2 - \phi_1 \right) \, \left( 1 + \frac{R_2}{R_1} \right) \, \frac{R_S}{R_G}$

In vorgefertigten integrierten Schaltungen sind die Widerstände R₁ und R₂ bereits fest vorgegeben. Die Verstärkung der Schaltung wird in diesem Fall über die Widerstände R_G und R_S eingestellt. Der Vorteil ist jedoch, dass die Stärke der Gleichtaktunterdrückung nicht von der Paarungstoleranz von R_G und R_S abhängig ist, wodurch man nicht auf speziell an die einzelne Schaltung angepasste (lasergetrimmte) Dünnschichtfilm-Widerstände angewiesen ist.

Aufbau in SC-Technik

Subtrahierer in Switched-Capacitor-Technik

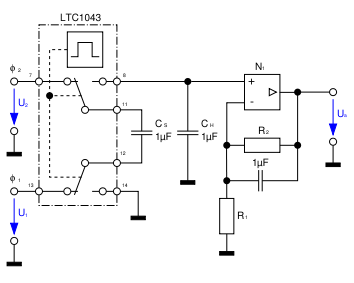
Das Prinzip eines Subtrahierers in Switched-Capacitor-Technik beruht darauf, dass zuerst ein Speicher-Kondensator C_S auf die zu messende Spannung aufgeladen wird. Anschließend wird die elektrische Ladung dieses Kondensators auf einen zweiten, einseitig gegen Masse geerdeten Halte-Kondensator C_H übertragen. Nach mehreren Schaltzyklen sowie ausreichender Lade- und Umladezeit liegt auf den beiden Kondensatoren die Differenzspannung an.

U_H = U_S = U_D = ϕ₂ − ϕ₁

Da der Halte-Kondensator gegen Masse geschaltet ist, tritt keine Gleichtaktspannung auf, wodurch die Spannung an dem zweiten Kondensator über einen einfachen Elektrometerverstärker ohne zusätzliche Differenzbildung verstärkt werden kann. Dadurch kann eine sehr hohe Gleichtaktunterdrückung erzielt werden.

Die Genauigkeit der Differenzbildung wird fast nur durch die Streukapazitäten der Schalter bestimmt. Um diese verhältnismäßig klein werden zu lassen, werden die Kondensatoren C_S und C_H möglichst groß gewählt (etwa 1 µF).

Mit dem integrierten Schalter LTC1043 von Linear Technology lässt sich so beispielsweise bis zu einer Frequenz von 20 kHz eine Gleichtaktunterdrückung von 120 dB erreichen (d. h., der Gleichtaktanteil wird um den Faktor 10⁶ reduziert).

Die Bandbreite der Schaltung wird durch drei Tiefpässe reduziert:

1. Aufladung des Speicherkondensators
2. Ladungsübertragung des Speicher- auf den Haltekondensator
3. Bandbreite des Verstärkers

Aufladung des Speicherkondensators

Die Ladezeit des Kondensators wird bestimmt durch:

• Kapazität des Speicherkondensators
• Widerstand der Schalter (2·240 Ω beim LTC1043)
• Innenwiderstand der Quelle

Ladungsübertragung des Speicher- auf den Haltekondensator

Vor der ersten Ladungsübertragung ist

U_H = 0,

nach der ersten Ladungsübertragung ist

$U_H = \frac{1}{2}\,U_D$,

nach der zweiten Ladungsübertragung ist

$U_H = \frac{3}{4}\,U_D$,

nach der dritten Ladungsübertragung ist

$U_H = \frac{7}{8}\,U_D$,

usw.. Die daraus resultierende Zeitkonstante entspricht daher etwa zwei Schaltzyklen. Um parasitäre Ladungen aus dem Schaltvorgang gering zu halten, werden niedrige Schaltfrequenzen von 500 Hz verwendet. Deshalb können mit dieser Schaltung nur niederfrequente Differenzsignale verarbeitet werden. Zudem können auch Frequenzen mit kleiner 10 bis 50 Hz nicht (korrekt) gemessen werden.

Bandbreite des Verstärkers

Auch die Bandbreite des Verstärkers reduziert die nutzbare Bandbreite. Über den zusätzlichen Kondensator an R₂ wird die Bandbreite des Verstärkers noch weiter herabgesetzt. In der Praxis wird dieser Kondensator so gewählt, dass die Bandbreite auf den zu messenden Frequenzbereich (rund 10 bis 50 Hz) reduziert wird, um höherfrequente Signale zu filtern und damit das Rauschen am Ausgang möglichst gering zu halten.

Subtrahiererbausteine

Legende für nebenstehende Tabelle

Typ	Aufbau
InAmp	Symmetrischer Elektrometersubtrahierer (Instrumentationsverstärker)
Diff	Aufbau mit Differenzverstärker
Asym	Asymmetrischer Aufbau
AsymS	Asymmetrischer Aufbau; einstellbar
HVSub	Hochspannungssubtrahierer
HVSubS	Hochspannungssubtrahierer; Verstärkung einstellbar
Anmerkung: Abkürzungen sind willkürlich gewählt

Integrierte Subtrahierer

Hersteller	ID	A	Ie	Uoffset	Typ	besondere Merkmale
Analog Devices	AD620	1…1k	0,5 nA	50 µV	Diff	günstiger Preis
	AD621	10, 100	0,5 nA	50 µV	Diff
	AD623	1…1k	17 nA	100 µV	InAmp	Rail-to-Rail Offset (RRO)
	AD624	1…1k	25 nA	25 µV	Asym	präzise
	AD629	1	2,5 µA V-1	200 µV	HVSubS	UGL = ±270 V
Linear Technology	LT1101	10, 100	6 nA	50 µV	Asym	Pb = 0,5 mW
	LT1102	10, 100	10 pA	200 µV		$\frac{\Delta U_a}{\Delta t} = 25 \, \frac{\mathrm{V}}{\mathrm{\mu s}}$
	LT1167	1…10k	100 pA	20 µV	InAmp	präzise
	LTC1100	100	25 pA	2 µV	Asym	Autozero-Funktion
National	CLC522	1…10	20 µA	25 µV	Diff	$\frac{\Delta U_a}{\Delta t} = 2 \, \frac{\mathrm{kV}}{\mathrm{\mu s}}$
Texas Instruments	INA103	1…100	2,5 µA	50 µV	InAmp	$U_r = 1 \, \frac{\mathrm{nV}}{\sqrt{\mathrm{Hz}}}$
	INA105	1	20 µA V-1	50 µV	HVSub
	INA106	10	50 µA V-1	50 µV
	INA110	1…5k	20 pA	50 µV	InAmp	$\frac{\Delta U_a}{\Delta t} = 17 \, \frac{\mathrm{V}}{\mathrm{\mu s}}$
	INA114	1…1k	1 nA	25 µV		präzise;
	INA116	1…1k	3 fA	2 mV		IB ≈ 3 fA
	INA118	1…10k	1 nA	20 µV		IB = 0,4 mA
	INA121	1…10k	4 pA	200 µV
	INA122	5…10k	10 nA	100 µV	AsymS	IB = 60 µA
	INA131	100	1 nA	25 µV	InAmp	präzise; günstiger Preis
	INA148	1	1 µA V-1	1 mV	HVSubS	UGL = ±200 V
	INA2141	10, 100	2 nA	20 µV	InAmp	2 Subtrahierer im IC
	PGA204	1…1k	2 nA	50 µV		Verstärkung digital einstellbar
	PGA207	1…10	2 pA	1 V

Literatur

• Ulrich Tietze, Christoph Schenk, Eberhard Gamm: Halbleiter-Schaltungstechnik, Springer 2002, 12. Auflage, ISBN 3540428496
• Walter G. Jung (Editor): OP AMP Applications, Firmenschrift Analog Devices 2002, ISBN 0916550265

Siehe auch

• Summierverstärker
• Trennverstärker

Fußnote

1. ↑ Diese Bezeichnung ist missverständlich, da sie auch für elektrische Musikinstrumente verwendet wird, siehe Gitarrenverstärker.