Symmetrische Irrfahrt

Die Random-Walk-Theorie (auch Theorie der symmetrischen Irrfahrt, wörtlich übersetzt Theorie der Zufallsbewegung) ist eine unmittelbare Folgerung der Markteffizienz-Theorie. Sie beschreibt den zeitlichen Verlauf von Marktpreisen (insbesondere von Aktienkursen und anderen Wertpapierpreisen) mathematisch.

Beschreibung

Nach der Random-Walk-Theorie lässt sich das Kurssignal nach den Lehren der Signaltheorie in den Trend und den Threshold zerlegen:

S(t) = T(t) + P(t) + U(t)

Dabei bedeutet S(t) das Signal, also der Kurs, T(t) den Driftanteil, P(t) den periodischen Anteil und U(t) einen unabhängigen Rauschanteil.

Der Driftanteil und der periodische Anteil werden zum Trend zusammengefasst, der sich durch Moving Averages beschreiben lässt. Er ist aufgrund der instantanen Manifestation aller Informationen gleich der Informations-Eingangsfunktion, d.h. dem wirklichen Informationsgehalt des Kurses. Dieser ist eine Zufallsfunktion, da keine Möglichkeit besteht, den zukünftigen Verlauf vorherzusagen.

Der Threshold ist hier gleichbedeutend mit U(t), dem unabhängigen Rausch-Anteil. Er wird in der Random-Walk-Theorie als informationslos angenommen. Es wird hier eine Brown'sche Bewegung postuliert.

Kritik an der Random-Walk-Theorie

Die Signalanalyse mittels Zeitreihenanalyse der Indizes wie beispielsweise Dax oder Dow Jones zeigt, dass der Threshold kein weißes Rauschen ist.

Zeitreihenanalyse des Threshold

Der Threshold ist nicht normalverteilt, sondern hat sog. "fat-tails", das heißt es besteht eine Leptokurtosis. Des Weiteren hat er keine quasi-konstante Amplitude: Es bestehen große Amplitudenschwankungen des Threshold, die sogenannte Volatilitätscluster bilden. Der Threshold ist eine Funktion des Rauschens mit Heteroskedastizität.

Eine gute Approximation des Thresholds ist indes durch die GARCH-Modelle gegeben. Allerdings gilt dies nur für die Vergangenheit, die Prognosefähigkeiten sind nicht besonders gut.

Vergleich mit allgemeinen Ansätzen

ARMA-Modelle nach Box-Jenkins weisen nach Otto Loistl best-fit-Approximations-Ansätze für die meisten DAX-Werte auf, die der Random-Walk-Theorie nicht entsprechen, da diese Ansätze 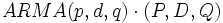$ARMA(p,d,q) \cdot (P,D,Q)$ nicht verschwindende p,q aufweisen.

Andere Ansätze

Alternativ zur Random-Walk-Theorie kann der Kursverlauf mit Markow-Ketten approximiert werden. (Also dem Ansatz einer Funktion mit vollständiger Vergesslichkeit).

Literatur

• Otto Loistl: Kapitalmarkttheorie. Oldenbourg Verlag, München 1994, ISBN 3-486-22968-0.