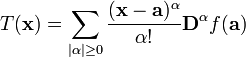- Taylornäherung
-
In der Analysis verwendet man Taylorreihen (auch Taylor-Entwicklungen oder Taylor-Näherung), um Funktionen in der Umgebung bestimmter Punkte durch Potenzreihen darzustellen. So kann ein komplizierter analytischer Ausdruck durch eine nach wenigen Gliedern abgebrochene Taylorreihe (oftmals gut) angenähert werden (z. B. in der Physik). Die Taylorreihe (oder Taylor-Reihe) einer Funktion f in einem Punkt ist die Potenzreihenentwicklung der Funktion an diesem Punkt. Sie ist benannt nach dem Mathematiker Brook Taylor. Eng verwandt mit der Taylorreihe sind die Taylor-Polynome, die im Artikel Taylor-Formel beschrieben sind.
Inhaltsverzeichnis
- 1 Definition
- 2 Eigenschaften
- 3 Beispiele
- 4 Taylorreihe in mehreren Variablen
- 5 Weblinks
- 6 Einzelnachweise
Definition
Sei I reelles Intervall und
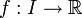 eine beliebig oft differenzierbare Funktion, dann heißt die unendliche Reihe
eine beliebig oft differenzierbare Funktion, dann heißt die unendliche Reihedie Taylor-Reihe von f mit Entwicklungspunkt a, wobei
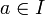 . Der Entwicklungspunkt ist der Punkt, in dessen Umgebung das Verhalten der Funktion interessiert. Die Konvergenz dieser Reihe wird hier nur als „formal“ angenommen (siehe dagegen Taylorformel mit Restglied).
. Der Entwicklungspunkt ist der Punkt, in dessen Umgebung das Verhalten der Funktion interessiert. Die Konvergenz dieser Reihe wird hier nur als „formal“ angenommen (siehe dagegen Taylorformel mit Restglied).Im Spezialfall a = 0 wird die Taylor-Reihe manchmal auch MacLaurin-Reihe genannt.
Hierbei bezeichnet f(n)(a) die n-te Ableitung von f an der Stelle a (mit f(0): = f) und
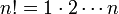 die Fakultät von n.
die Fakultät von n.Den Ausdruck
(also die Summe der ersten beiden Terme der Taylorreihe) nennt man auch "Linearisierung von f an der Stelle a". Allgemeiner nennt man die Partialsumme
die für festes a ein Polynom in der Variablen x darstellt, das n-te Taylorpolynom.
Die schon erwähnte Taylorformel mit Restglied macht Aussagen darüber, wie dieses Polynom von der Funktion f abweicht. Aufgrund der Einfachheit der Polynomdarstellung sowie der guten Anwendbarkeit der Restgliedformeln sind Taylorpolynome unverzichtbares Hilfsmittel der Analysis, der Physik und der Ingenieurwissenschaften geworden.
Eigenschaften
Die Taylorreihe ist eine Potenzreihe in x. Im Fall einer analytischen Funktion f hat die Taylor-Reihe in jedem Punkt a einen positiven Konvergenzradius und stimmt in ihrem Konvergenzbereich mit f überein, d. h. es gibt ein r > 0, sodass für | x − a | < r gilt
Diese Aussage gilt jedoch nicht für beliebige unendlich oft differenzierbare Funktionen. Es gibt Taylor-Reihen mit Konvergenzradius 0 und es gibt unendlich oft differenzierbare Funktionen, deren Taylorreihe im Punkt a einen positiven Kovergenzradius hat, jedoch in keiner Umgebung von a mit f übereinstimmt (siehe Beispiel unten). Aber auch in solchen Fällen wird die Reihe als Taylorreihe bezeichnet.
Beispiele
Taylorreihen mit Konvergenzradius größer Null
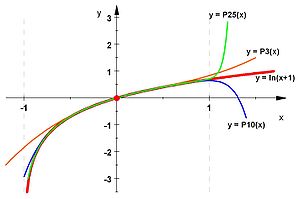
Viele bekannte Funktionen lassen sich durch Potenzreihen darstellen, die dann gleichzeitig Taylorreihen der Funktion sind. Zum Beispiel gilt für alle reellen Zahlen x:
Exponentialfunktionen und Logarithmen
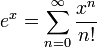 für alle reellen (oder komplexen) x
für alle reellen (oder komplexen) x
Diese Formel ist jedoch für praktische Rechnungen ungeeignet. Schneller konvergiert diese Reihe:
Wählt man
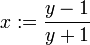 für ein y > 0, dann erhält man damit ln(y).
für ein y > 0, dann erhält man damit ln(y).Trigonometrische Funktionen
Für den Entwicklungspunkt a = 0 gilt (Maclaurin-Reihe):
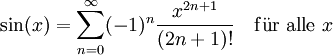
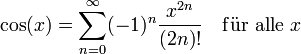
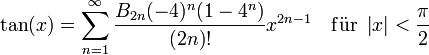 , dabei ist B2n die 2n-te Bernoulli-Zahl.
, dabei ist B2n die 2n-te Bernoulli-Zahl.
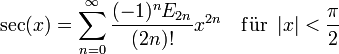 , dabei ist E2n die 2n-te Eulersche Zahl.
, dabei ist E2n die 2n-te Eulersche Zahl.
Einige häufig verwendete Näherungen
In den Natur- und Ingenieurwissenschaften werden manchmal folgende Reihenentwicklungen verwendet (ohne Beweis):
Eine Funktion, die sehr schlecht durch die Taylorreihe approximiert wird
Die Taylorreihe einer Funktion konvergiert nicht immer gegen die Funktion. Im folgenden Beispiel stimmt die Taylorreihe auf keiner Umgebung um den Entwicklungspunkt x = 0 mit der Ausgangsfunktion überein:
Als reelle Funktion ist f beliebig oft stetig differenzierbar, wobei die Ableitungen in jedem Punkt
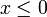 (insbesondere für x = 0) ausnahmslos 0 sind. Die Taylorreihe um den Nullpunkt ist also die Nullfunktion, und stimmt in keiner Umgebung der 0 mit f überein. Daher ist f nicht analytisch. Die Taylorreihe um einen Punkt a > 0 konvergiert zwischen 0 und 2a gegen f. Auch mit einer Laurentreihe lässt sich diese Funktion nicht approximieren, weil die Laurentreihe, die die Funktion für x > 0 korrekt wiedergibt, für x < 0 nicht konstant 0 ergibt.
(insbesondere für x = 0) ausnahmslos 0 sind. Die Taylorreihe um den Nullpunkt ist also die Nullfunktion, und stimmt in keiner Umgebung der 0 mit f überein. Daher ist f nicht analytisch. Die Taylorreihe um einen Punkt a > 0 konvergiert zwischen 0 und 2a gegen f. Auch mit einer Laurentreihe lässt sich diese Funktion nicht approximieren, weil die Laurentreihe, die die Funktion für x > 0 korrekt wiedergibt, für x < 0 nicht konstant 0 ergibt.Eine Funktion, deren Taylorreihe Konvergenzradius 0 hat
Die Funktion
ist auf ganz
 beliebig oft differenzierbar, aber ihre Taylorreihe in a = 0 ist
beliebig oft differenzierbar, aber ihre Taylorreihe in a = 0 istund somit nur für x = 0 konvergent.[1]
Taylorreihe in mehreren Variablen
Die Taylorreihe kann auch in allgemeiner Form für Funktionen in mehreren Variablen geschrieben werden:
wobei die partiellen Ableitungen nach dem ersten (zweiten, ...) Funktionsargument an der Stelle
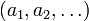 zu nehmen sind. Zum Beispiel ist die Taylorreihe zweiter Ordnung einer Funktion, die von den beiden Variablen x und y abhängt, in der Umgebung (a, b):
zu nehmen sind. Zum Beispiel ist die Taylorreihe zweiter Ordnung einer Funktion, die von den beiden Variablen x und y abhängt, in der Umgebung (a, b):Die Taylorreihe zweiter Ordnung einer skalarwertigen Funktion in mehr als einer Variable kann kompakter geschrieben werden als:
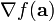 ist der Gradient und
ist der Gradient und 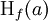 die Hesse-Matrix.
die Hesse-Matrix.In der Multiindex-Notation wird die Taylorreihe in mehreren Variablen zu:
in voller Entsprechung zum eindimensionalen Fall.
Dies lässt sich noch prägnanter in der Form
![T(\mathbf x)=\exp [(x_1- a_1)\,\partial_1]\cdot\exp [(x_2-a_2)\,\partial_2 ]\cdot\dots\,
f(\mathbf a )](/pictures/dewiki/101/e3fef975422528ea7184960f574a2503.png) schreiben, was direkt zur ersten Formel dieses Abschnitts führt. Dabei ist vorausgesetzt, dass die Funktion T erstens im fraglichen Bereich existiert und unendlich oft stetig-differenzierbar ist und zweitens durch die Reihe definiert werden kann. In vielen Fällen ist sie dann identisch mit f, d.h. dass das oben erwähnte Restglied im limes
schreiben, was direkt zur ersten Formel dieses Abschnitts führt. Dabei ist vorausgesetzt, dass die Funktion T erstens im fraglichen Bereich existiert und unendlich oft stetig-differenzierbar ist und zweitens durch die Reihe definiert werden kann. In vielen Fällen ist sie dann identisch mit f, d.h. dass das oben erwähnte Restglied im limes  verschwindet.
verschwindet.Weblinks
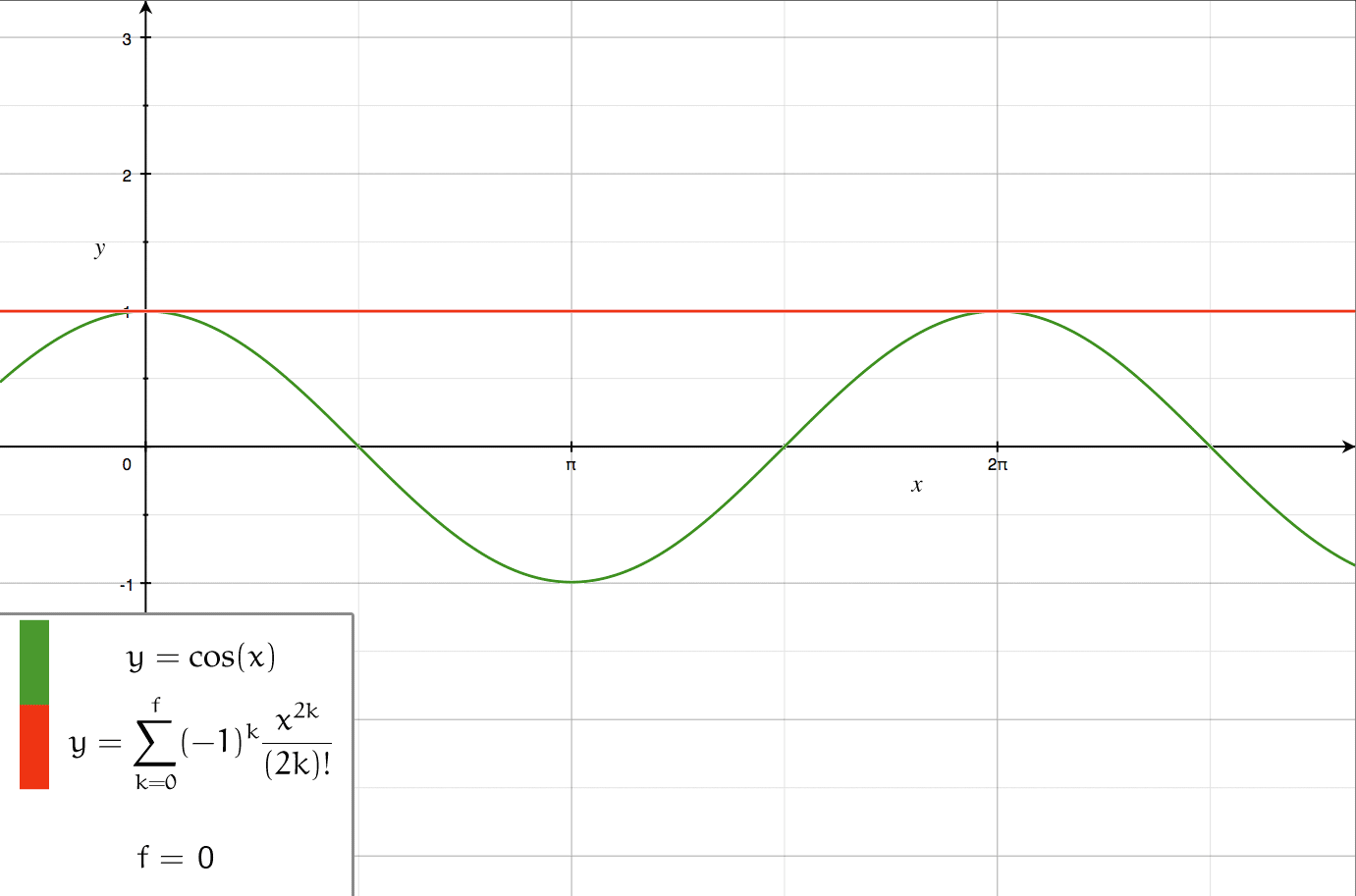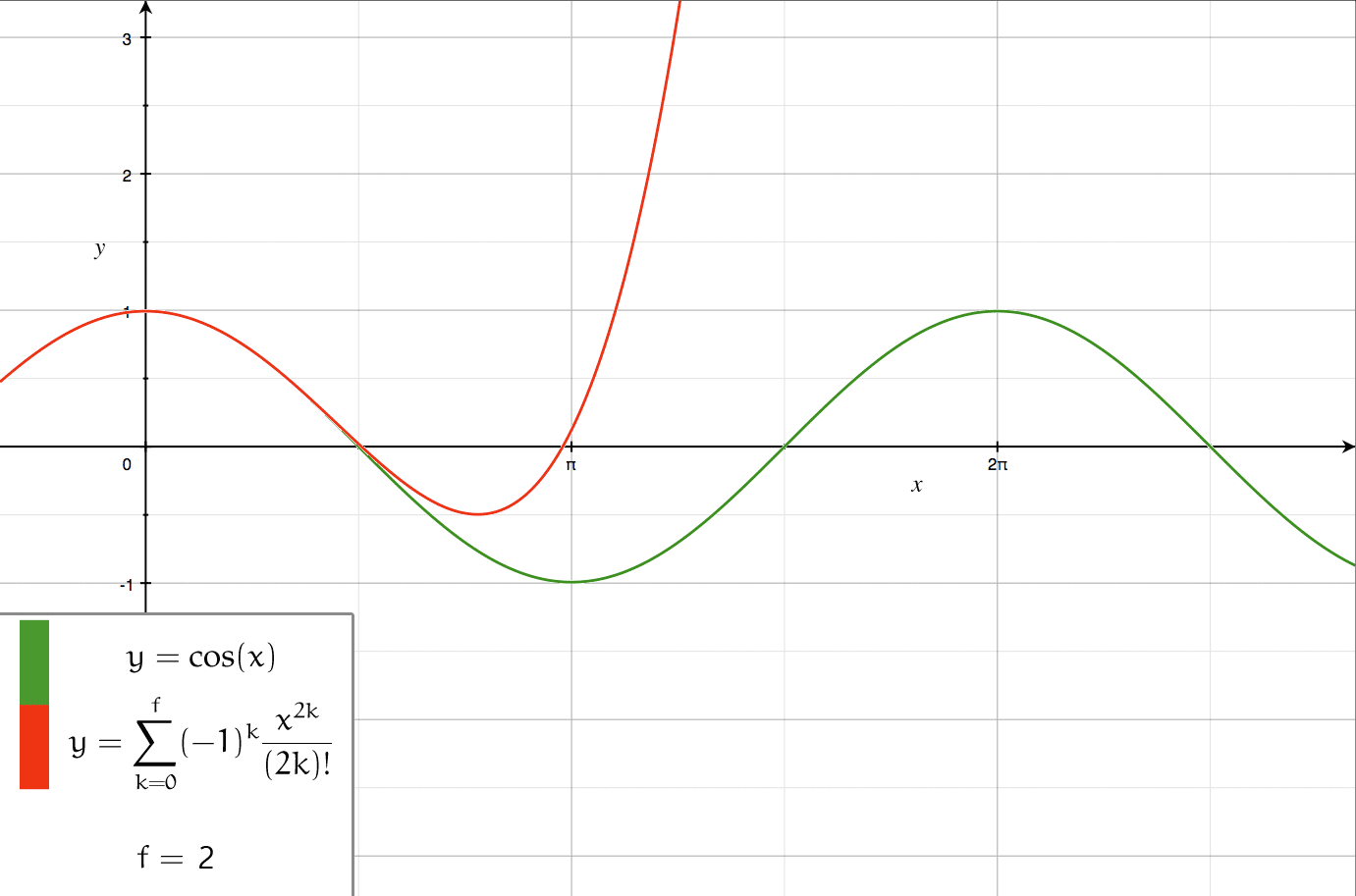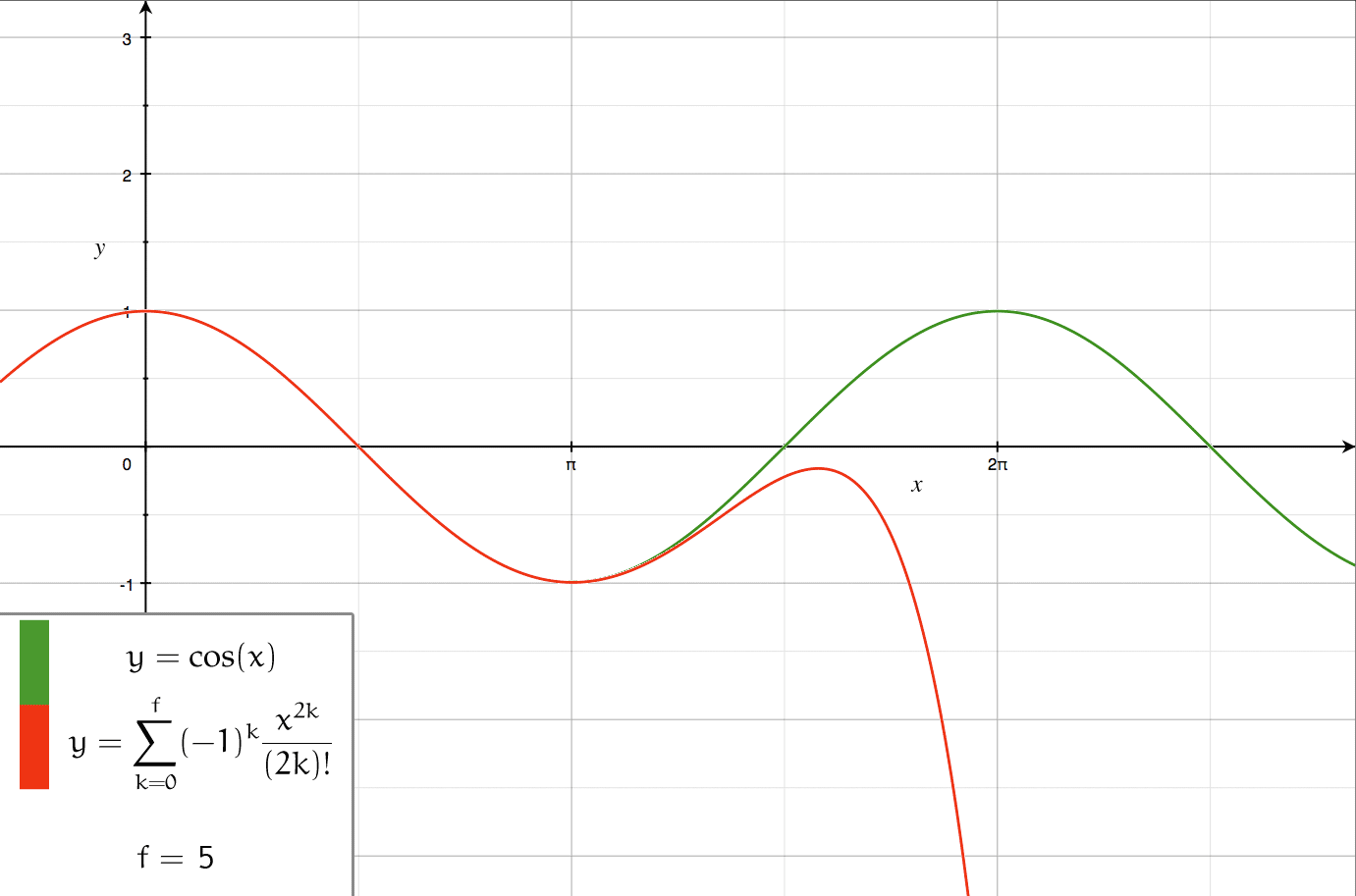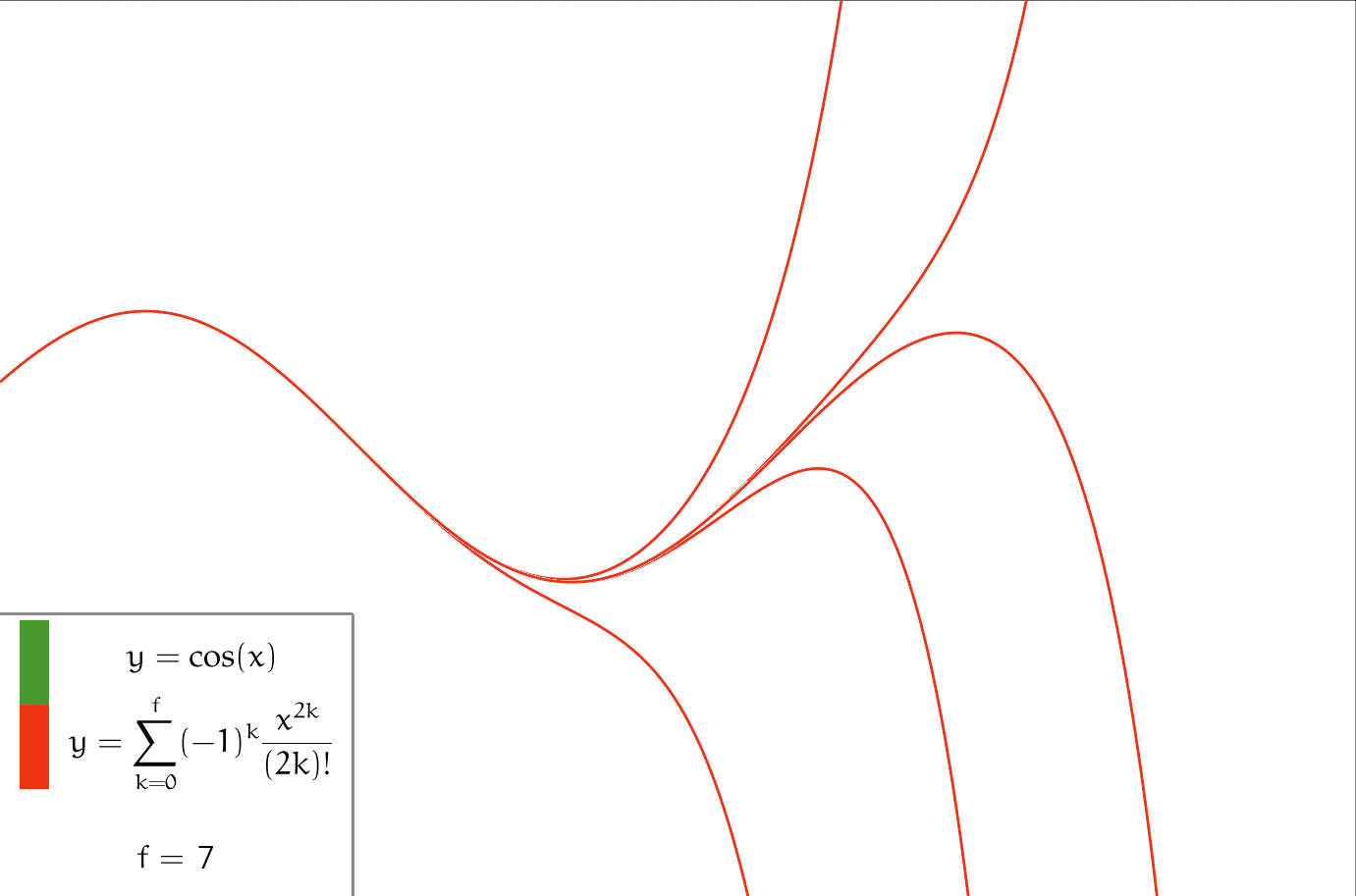
- Visualisierung der Taylorreihen-Entwicklung - Der Grad der Näherung und der Ableitpunkt kann dabei selbst bestimmt werden. Die Stammfunktion ist eine Sinuskurve.
- Taylor Series auf MathWorld (englisch)
- Real and Complex Taylor Series auf PlanetMath (englisch)
Einzelnachweise
Wikimedia Foundation.

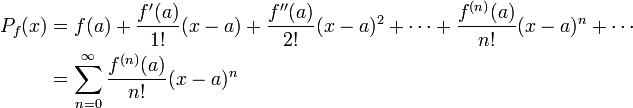
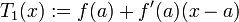
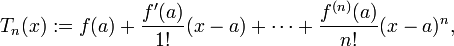
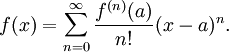
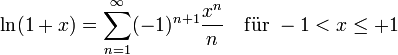
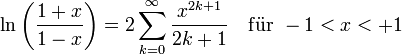

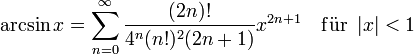
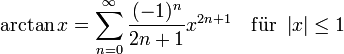
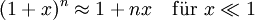
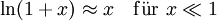
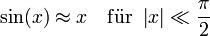
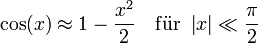
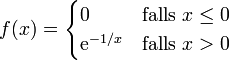
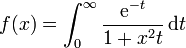
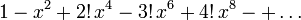
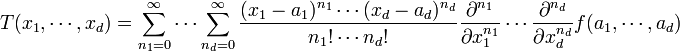
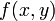
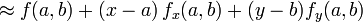
![+ \frac{1}{2}\left[ (x-a)^2\, f_{xx}(a,b) + 2(x-a)\,f_{xy}(a,b)\,(y-b) + (y-b)^2\, f_{yy}(a,b) \right].](/pictures/dewiki/50/254101c5ea59e30c15f9f0202847edb2.png)