- Unterabtastung
-
Unter der Unterabtastung (englisch undersampling) wird in der Signalverarbeitung die Abtastung eines Signalverlaufes mit weniger als der doppelten Bandbreite verstanden. Unter bestimmten Voraussetzungen wird dabei nicht das Nyquist-Shannon-Abtasttheorem verletzt und die Unterabtastung kann in diesem Fall dazu dienen, ein hochfrequentes Signal mittels Unterabtastung in einen Frequenzbereich mit geringer Frequenz zu versetzen. Bei Verletzung des Nyquist-Shannon-Abtasttheorems tritt zufolge der Unterabtastung Aliasing und damit einhergehend Informationsverlust auf. Die Unterabtastung stellt das Gegenstück zur Überabtastung (oversampling) dar.
Inhaltsverzeichnis
Verfahren
Ein Signal in Bandpasslage weist allgemein eine Bandbreite B um die symmetrische Mittenfrequenz f0 auf. Um das Nyquist-Shannon-Abtasttheorems nicht zu verletzen, darf das Signal außerhalb der Bandbreite keine Frequenzanteile aufweisen. Dies kann unter anderem durch Bandpassfilter vor der Unterabtastung gewährleistet werden.
Mit der Abtastfrequenz fA verschieben alle Abtastfrequenzen
die Mittenfrequnz f0 des Bandpasssignals auf die wählbare Bildfrequenz f'0 im Basisband. Der Wert r stellt den Faktor der Unterabtastung dar, mit größer werdendem r werden die Abtastfrequenzen und somit nutzbaren Basisbandbreiten immer kleiner.
Die Bildfrequenz f'0 im Basisband wird üblicherweise bei symmetrischem Bandspektrum auf den Wert f'0 = 0 festgelegt. Bei unsymmetrischen Bandspektren wird
 gewählt.
gewählt.Unterabtastung bei symmetrischem Bandspektrum
Bei symmetrischen Bandspektrum, d.h. die Information im Bandpasssignal steht doppelt und symmetrisch um f0 zur Verfügung wie es beispielsweise bei der Amplitudenmodulation vorliegt, wird f'0 = 0 gewählt, womit die Abtastfrequenzen:
zur Verfügung stehen. Die minimale Abtastfrequenz muss größer als die Bandbreite B sein, womit sich mit dieser Nebenbedingung dann der Faktor r bestimmten lässt zu:
Damit entspricht die Unterabtastung bei dem symmetrischem Bandspektrum der Demodulation einer Amplitudenmodulation.
Unterabtastung bei asymmetrischem Bandspektrum
Bei asymmetrischen Bandspektren, wie dies beispielsweise bei der Einseitenbandmodulation der Fall ist, liegen keine negative Frequenzen vor, das Bandpasssignal kann damit nicht mittels Unterabtastung in Basisbandlage gebracht werden sondern nur in eine niedrigere Zwischenfrequenzlage zur weiteren Verarbeitung. Die Funktion entspricht dem eines Mischers.
Bei asymmetrischem Bandspektrum wird zur Einhaltung des Nyquist-Shannon-Abtasttheorems
 gewählt, womit folgende die Abtastfrequenzen zur Verfügung stehen:
gewählt, womit folgende die Abtastfrequenzen zur Verfügung stehen:Die minimale Abtastfrequenz muss größer als die doppelte Bandbreite B sein, womit sich mit dieser Nebenbedingung dann der Faktor r bestimmten lässt zu:
- Beispiel
Es soll das gesamte für UKW-Rundfunk genutzte Frequenzband von 88 MHz bis 110 MHz, mit einer Bandbreite B von 22 MHz, mittels Unterabtastung in den Zwischenfrequenzbereich von 0 MHz bis 22 MHz in Regelllage verschoben werden, wie in der Abbildung rechts dargestellt.
Die Mittenfrequenz f0 des Bandes beträgt 99 MHz, die Abtastfrequenz fA muss mindestens 44 MHz oder mehr betragen. Mit r = 2 ergibt sich die somit die in diesem Fall einzige mögliche Abtastfrequenz zu:
Die eigentliche Demodulation eines bestimmten Radioprogrammes erfolgt erst durch die nachgeschaltene digitale Demudolatorstufe, welche den Vorteil hat die Demodulation in dem deutlich geringeren Frequenzband von 0 MHz bis 22 MHz und somit geringerer Taktrate ausführen zu können.
Verletzung des Abtasttheorems
Bei nicht bandlimitierten Signalen in Bandpasslage führt die Unterabtastung zu einer Verletzung des Nyquist-Shannon-Abtasttheorems:
- Informationsverlust, nicht alle Bestandteile des Originalsignals werden reproduziert (Bandpass)
- Spiegelfrequenzen oder Aliasing treten als störende Bestandteile auf.
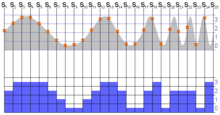
Die graue Schwingung sei das analoge Signal, das diskretisiert (z. B. digitalisiert) werden soll. Die blauen Zahlen rechts geben den Wertebereich an. Ein Sample, das in diesen Bereich fällt, erhält diese digitale Zahl zugeordnet (Quantisierung). Die senkrechten Linien (S1 bis S25) geben die Zeitpunkte an, zu denen abgetastet wird. Die roten × verdeutlichen, in welchen Wertebereich das jeweilige Sample fällt. Die rechteckige blaue Signalform repräsentiert das aus den digitalen Daten gewonnene Signal. (Ehe es einem Rekonstruktionsfilter zugeführt wird.)
In der Abbildung ist zu erkennen, dass ab Sample 20 (S20) die digitalisierten Werte die abgetastete Frequenz nicht mehr repräsentieren. Das Signal wird daher mit einer deutlich geringeren Frequenz rekonstruiert.
Literatur
- Fernando Puente León, Uwe Kiencke, Holger Jäkel: Signale und Systeme. 5. Auflage. Oldenbourg, 2011, ISBN 978-3-486-59748-6.
Wikimedia Foundation.