Mischer (Elektronik)

Mischer (englisch: mixer) werden in der Kommunikationstechnik zur Frequenzumsetzung (englisch frequency conversion) von elektrischen Signalen verwendet. Sie bestehen meist aus nichtlinearen Bauelementen wie Dioden oder nichtlinearen Verstärkern wie Transistoren. Im Rahmen der digitalen Signalverarbeitung kann man Mischer auch durch Software in einem Signalprozessor nachbilden. Mischung lässt sich auch durch Unterabtastung erreichen.

Davon zu unterscheiden ist die additive Zusammenführung verschiedener Signalquellen in einem Mischpult - bei diesem ist Frequenzumsetzung, außer bei Sondereffekten, unerwünscht.

Prinzip eines idealen multiplikativen Mischers mit nur zwei Ausgangsfrequenzen.

Anwendungen

Bei Empfängern spricht man von Umsetzen oder Heruntermischen, wenn ein hochfrequentes Nutzsignal in einem Überlagerungsempfänger mittels eines Oszillator-Signals auf eine niederfrequentere Zwischenfrequenz gemischt wird. Beispiel: Das Signal von Kommunikationssatelliten muss noch im LNB der Parabolantenne von 11 GHz auf etwa 2 GHz heruntergemischt werden, weil es sonst nicht durch Koaxkabel übertragen werden kann. Im eigentlichen Empfänger wird die Frequenz in weiteren Mischern meist noch weiter herabgesetzt, weil diese dann einfacher verstärkt und gefiltert werden kann.

Bei manchen Modulationsarten wie SSB kann die Nachricht (Sprache) nur durch einen Mischer wieder gewonnen werden. Bei Sendern erfolgt die Modulation häufig zunächst auf einer tiefen Frequenz, weil hier Erzeugung und Prüfung der Qualität einfacher sind. Diese wird dann in einem Mischer auf die höhere Sendefrequenz heraufgesetzt (siehe Exciter (Radar)).

Bei einem Chopper-Verstärker wird ein sehr niederfrequentes Signal durch einen „Chopper“ auf eine wesentlich höhere Frequenz transponiert, weil diese problemloser verstärkt werden kann. Anschließend wird es mit einem zweiten Mischer wieder demoduliert.

In Synchrondemodulator und Lock-in-Verstärker wird die zu messende Wechselspannung bekannter Frequenz auf eine erheblich tiefere Frequenz (fast Gleichspannung) heruntergemischt und dann schmalbandig gefiltert. Dadurch lassen sich Störspannungen abweichender Frequenz eliminieren. Das Prinzip entspricht einem Direktmischempfänger.

Im Musikinstrument Theremin entsteht die Niederfrequenz durch Mischung der Ausgangssignale zweier Hochfrequenzoszillatoren unterschiedlicher Frequenz.

Prinzip eines Mischers

Ausgangsspektrum eines Mischers mit quadratischer Kennlinie. Die Eingangsfrequenzen sind 34 kHz und 653 kHz

Ausgangsspektrum eines Röhrenmischers mit anderer Kennlinie. Die Eingangsfrequenzen sind 34 kHz und 653 kHz

Ein Mischer verarbeitet zwei Eingangssignale:

• Die umzusetzende Wechselspannung, das eigentliche „Eingangssignal“ mit der Frequenz f_e. Dieses Signal ist der eigentliche Informationsträger, es enthält die Nutzinformation in Form einer Modulation.
• ein Hilfssignal, das sog. Lokaloszillatorsignal mit der Frequenz f_LO. Dieses wird in aller Regel als sinus- oder rechteckförmiges Signal lokal erzeugt.

Der Mischer produziert daraus ein Ausgangssignal, das stets mehrere Frequenzen enthält. Zwei Anteile, die beiden „Seitenbänder“, sind erwünscht. Sie enthalten die Modulation des umzusetzenden Signals, haben aber andere Frequenzen. Im Regelfall wird eines der Seitenbänder durch Filter zu den nachfolgenden Verstärkerstufen durchgelassen. Je nach Qualität erzeugt der Mischer aber auch andere Frequenzanteile unterschiedlicher Amplitude, die als unerwünschte Mischprodukte bezeichnet und ebenfalls unterdrückt werden müssen.

Im oberen Bild ist das Frequenzspektrum eines qualitativ hochwertigen Gegentaktmischers aus zwei Feldeffekttransistoren gezeigt. Beide Eingangsfrequenzen f_e = 34 kHz und f_LO = 653 kHz gelangen wegen der Symmetrie der Schaltung nicht zum Ausgang. Dort kann man nur die Harmonischen, also die doppelten Frequenzen messen und die beiden Seitenbänder mit den Frequenzen f_LO+f_e = 687 kHz bzw. f_LO-f_e = 619 kHz. Bei einem idealen multiplizierenden Mischer wären nur die beiden Seitenbänder vorhanden.

Das untere Bild zeigt das Spektrum, das eine Elektronenröhre als Mischer aus den gleichen Eingangssignalen auf Grund ihrer anders gekrümmten Kennlinie erzeugt. Die beiden stärksten, unerwünschten Anteile sind die Eingangsfrequenzen f_e und f_LO. Neben deren Harmonischen werden bei diesem Mischer weitere unerwünschte Mischprodukte erzeugt, die zum Teil recht nahe bei den gewünschten Seitenbändern liegen und durch erhöhten Filteraufwand unterdrückt werden müssen. Vergleicht man dieses Spektrum mit der folgenden Formel, erkennt man, dass die Bezeichnung „Multiplikativer Mischer“ grob irreführend ist.

Mathematische Darstellung

Das Funktionsprinzip eines Mischers basiert darauf, dass zwei (oder mehr) Eingangssignale sich in ihrer Amplitude gegenseitig beeinflussen, idealerweise miteinander multipliziert werden. Bei zwei Signalen spricht man hierbei meist davon, dass das niederfrequentere Signal dem höherfrequenten Signal aufmoduliert wird. Die Eignung der Multiplikation als Signalverarbeitungsmethode der Wahl beruht auf der Identität

$a_1 \cos{ \left( {\omega}_\mathrm{e}t + {\varphi}_\mathrm{e} \right) } \cdot 2a_2 \cos{ \left( {\omega}_\mathrm{LO}t \right) } = a_1 a_2 \left[ \cos{ \left( \left( {\omega}_\mathrm{e} + {\omega}_\mathrm{LO} \right) t + {\varphi}_\mathrm{e} \right) } + \cos{ \left( \left( {\omega}_\mathrm{e} - {\omega}_\mathrm{LO} \right) t + {\varphi}_\mathrm{e} \right) }\right]$

mit

${\omega}_\mathrm{LO} := 2\pi f_\mathrm{LO}\$

In diesem Spezialfall einer reinen Sinusschwingung im Eingang, erfüllt ersichtlich jedes der beiden Ausgangssignale rechts - nach Ausfilterung des anderen - die Aufgabenstellung. Der Fall eines allgemeineren Eingangssignals wird via Spektralanalyse (Fourieranalyse) mit umfasst.

Zum Beispiel ist auch der Amplituden-Modulator eines AM-Senders tatsächlich nichts anderes als ein Mischer, bei dem Summen- und Differenzfrequenzen von Sender-Trägerfrequenz und Audiospektrum entstehen. Diese sog. Seitenbänder der Sendung bilden das eigentliche Nutzsignal der Sendung, während das Trägersignal selbst - von der Empfangsfeldstärke einmal abgesehen - keine Information überträgt.

Beim Mischen eines Audiosignales mit einer konstanten Frequenz verschiebt sich das Spektrum des Signals auf der Frequenzachse: die Bandbreite des Nutzsignals ändert sich durch die Umsetzung nicht, wohl aber ändern sich die relativen Verhältnisse der Frequenzen der Signalanteile, und damit die Harmonien. Praktisch erfahrbar ist dies z. B. beim Abhören von SSB-Kurzwellensendungen, die zur Wiedergabe (vereinfacht gesagt) mit einem auf die Trägerfrequenz des Senders abzustimmenden LO gemischt werden. Im Gegensatz dazu spreizt oder staucht ein in anderer Geschwindigkeit abgespieltes Tonband das Spektrum des Nutzsignals, die Harmonien bleiben jedoch erhalten.

Ein idealer Mischer entspricht einem Analogmultiplizierer und wird daher als Produktmodulator bezeichnet. Er hat, wie oben beschrieben, zwei Eingänge und einen Ausgang und bildet das Ausgangssignal aus dem Produkt der beiden Eingangssignale. Bei einem idealen, symmetrischen Mischer erscheinen die Frequenzen f_e bzw. f_LO der Eingangssignale selbst nicht am Ausgang, sondern das Ausgangssignal besteht nur aus den Summen- und Differenzsignalen mit den Frequenzen f_e+f_LO und f_e-f_LO. Bei realen (unvollkommenen) Mischern entstehen am Ausgang weitere (unerwünschte) Frequenzanteile, die durch geeignete Filter (z. B. Bandpass) eliminiert werden müssen.

Für den Fall, dass das Eingangssignal auf eine höhere Frequenz umgesetzt wird (Summenbildung), spricht man von einem Aufwärtsmischer (engl.: up-converter), andernfalls (Differenzbildung) von einem Abwärtsmischer (engl.: down-converter).

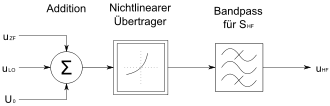
Additive Mischung

Prinzipschaltbild eines additiven Mischers

Die „additive“ Mischstufe ist – genau genommen – ein signalverzerrender Analog-Addierer. Die Signale werden auf ein Bauteil mit nichtlinearer Strom/Spannungs-Kennlinie geführt, dabei entstehen unter anderem Summe und Differenz der Signalfrequenzen. Als nichtlineare Kennlinie wird meist die nichtlineare Strom-Spannungs-Kennlinie einer Diode oder eines Transistors verwendet. Das Eingangssignal ist hierbei eine Spannung, das Ausgangssignal ein Strom.

Die Kennlinie wird durch eine Taylor-Reihe im Arbeitspunkt AP(U₀) dargestellt.

$I(U)=\sum\limits_{n=0}^{\infty }\left[ \frac{1}{n!} \frac{\partial ^{n}I}{\partial U^{n}} {\Bigg|}_{U_{0}} \left( U-U_{0}\right) ^{n}\right]$

Damit wird der Effekt des Inputs der Summe U₁ + U₂:

$I(U_0 + U_1 + U_2) - I(U_0) = \frac{\partial I}{\partial U} {\Bigg|}_{U_{0}} \left( U_1+U_2 \right) + \frac{\partial ^{2}I}{\partial U^{2}} {\Bigg|}_{U_{0}} \left( U_1^2/2 + U_1U_2 + U_2^2/2 \right) +$ Terme höherer Ordnung

Um hieraus den gewünschten Beitrag U₁U₂ zu isolieren, müssen die u. U. deutlich größeren Anteile U₁, U₂, U₁², U₂² herausgefiltert werden, und die Anteile höherer Ordnung müssen gering genug sein, um Vernachlässigung zuzulassen.

Multiplikative Mischung

Prinzip der multiplikativen Mischung

Bei der multiplikativen Mischung wird das ZF-Signal mit dem LO-Signal multipliziert. Das kann zum Beispiel durch einen mit einem Signal regelbaren Verstärker (z.B. eine Mischröhre (Heptode) oder einem Feldeffekttransistor mit zwei Gates) geschehen oder mit einer Logarithmierung, nachfolgenden Addition und anschließender Ent-Logarithmierung (Exponentialfunktion).

Die gewünschte HF-Frequenz muss hierbei mit einem Bandpass herausgefiltert werden. Das Signal s_M(t) am Ausgang des Multiplizierers erhält man durch Fourierreihenentwicklung des LO-Signals:

$s_\mathrm{M}(t)= s_\mathrm{ZF}(t)\cdot s_\mathrm{LO}(t)= s_\mathrm{ZF}(t)\cdot \left[ c_{0}+\sum \limits_{n=1}^{\infty }c_{n}\cos \left( n\cdot \omega _\mathrm{LO}\cdot t+\varphi _{n}\right) \right]$

Das ZF-Signal wird dabei mit der Grundwelle c₁ und den Oberwellen c₁, c₂,…, c_n multipliziert. Der Gleichanteil c₀ wird direkt übertragen. Dabei wird oft kein sinusförmiges, sondern ein rechteckförmiges LO-Signal mit f_LO als Grundfrequenz verwendet.

Begriffe

• Die Zwischenfrequenz (ZF-Frequenz oder englisch: intermediate frequency, IF-Frequency) mit dem Formelzeichen f_ZF ist die niedrigere Trägerfrequenz.
• Die Hochfrequenz (HF-Frequenz oder englisch: radio frequency, RF-Frequency) mit dem Formelzeichen f_HF ist die höhere Trägerfrequenz.
• Die Lokaloszillatorfrequenz (LO-Frequenz oder englisch: local oszillator frequency) mit dem Formelzeichen f_LO entspricht dem Frequenzversatz der Umsetzung.

Die Signale werden dementsprechend als ZF-, HF- und LO-Signale (s_ZF, s_HF und s_LO) bezeichnet.

Aufwärtsmischer

Frequenzspektrum bei einem Aufwärtsmischer

Beim Aufwärtsmischer wird am Eingang das ZF-Signal angelegt und mit dem LO-Signal multipliziert.

$s_\mathrm{ZF}(t) = i(t) \cdot \cos{ \left( {\omega}_\mathrm{ZF} \cdot t \right) } - q(t) \cdot \sin{\left( {\omega}_\mathrm{ZF} \cdot t \right)} = a(t) \cos{ \left[ {\omega}_\mathrm{ZF} \cdot t + {\varphi}(t) \right] }$

$s_\mathrm{LO}(t) = 2 \cos{ \left( {\omega}_\mathrm{LO} \cdot t \right) }$

Im Weiteren wird nur die Darstellung mit der Amplitudenmodulation a(t) und der Winkelmodulation ϕ(t) angegeben, da diese kürzer ist als die Darstellung mit den Quadraturkomponenten.

Am Ausgang erhält man das HF-Signal s_HF.

$s_\mathrm{HF}(t) = s_\mathrm{ZF}(t) \cdot s_\mathrm{LO}(t) = a(t) \cos{ \left[ {\omega}_\mathrm{ZF} \cdot t + {\varphi}(t) \right] } \cdot 2 \cos{ \left( {\omega}_\mathrm{LO} \cdot t \right) }$

$\begin{matrix} s_\mathrm{HF}(t)={} & \underbrace{a(t) \cos \left[ \left( {\omega}_\mathrm{LO}+\omega _\mathrm{ZF} \right) \cdot t+\varphi (t) \right] } & {+} & \underbrace{a(t) \cos \left[ \left( {\omega}_\mathrm{LO}-\omega _\mathrm{ZF} \right) \cdot t-\varphi (t) \right] } \\ {} & {{\rm Oberband \, \left( f > f_\mathrm{LO} \right) }} & {} & {\rm Unterband \, \left( f < f_\mathrm{LO} \right)} \\ {} & {\rm in \, Gleichlage} & {} & {\rm in \, Kehrlage} \end{matrix}$

Der als Oberband bezeichnete Anteil weist dieselbe Frequenzfolge auf wie das ZF-Signal (f_LO+f_ZF). Dies wird als Gleichlage bezeichnet. Das Unterband weist eine zum ZF-Signal invertierte Frequenzfolge auf (f_LO-f_ZF). Dies wird als Kehrlage bezeichnet. Jedes dieser Bänder kann als Ausgangssignal verwendet werden, das jeweils andere wird mit einem Filter unterdrückt. Aufwärtsmischer werden in Sendern und in Chopper-Verstärkern verwendet.

Abwärtsmischer

Abwärtsmischer in Gleichlage (f_HF > f_LO)

Abwärtsmischer in Kehrlage (f_HF < f_LO)

Beim Abwärtsmischer wird am Eingang ein HF-Signal angelegt und mit dem LO-Signal multipliziert.

$s_\mathrm{HF}(t) = a(t) \cos{ \left[ {\omega}_\mathrm{HF} \cdot t + {\varphi}(t) \right] }$

$s_\mathrm{LO}(t) = 2 \cos{ \left( {\omega}_\mathrm{LO} \cdot t \right) }$

Am Ausgang erhält man das Signal s_M:

$s_M(t) = s_\mathrm{HF} \left( t \right) \cdot s_\mathrm{LO}(t) = a(t) \cos{ \left[ \omega _\mathrm{HF} \cdot t + \varphi (t) \right] } \cdot 2 \cos{\left( \omega _\mathrm{LO} \cdot t \right)}$

$s_\mathrm{M}(t) = \begin{cases} \begin{matrix} a(t)\cos \left[ \left( \varpi _\mathrm{HF}+\omega _\mathrm{LO}\right) \cdot t+\varphi (t) \right] \\ {}+a(t)\cos \left[ \left( \varpi _\mathrm{HF}-\omega _\mathrm{LO}\right) \cdot t+\varphi (t)\right] \end{matrix} & {\rm Gleichlage} \, (f_\mathrm{HF}>f_\mathrm{LO}) \\ \begin{matrix} a(t)\cos \left[ \left( \varpi _\mathrm{HF}+\omega _\mathrm{LO}\right) \cdot t+\varphi (t) \right] \\ {}+a(t)\cos \left[ \left( \varpi _\mathrm{LO}-\omega _\mathrm{HF}\right) \cdot t-\varphi (t)\right] \end{matrix} & {\rm Kehrlage} \, (f_\mathrm{LO}>f_\mathrm{HF}) \end{cases}$

Wenn die HF-Frequenz größer ist als die LO-Frequenz, erhält man ein ZF-Signal in Gleichlage mit gleicher Frequenzfolge. Andernfalls ein ZF-Signal in Kehrlage mit invertierter Frequenzfolge. Das Signal s_M setzt sich zusammen aus dem Signal s_ZF (links) und einem Signal mit f_HF + f_LO (rechts). Letzteres wird nicht benötigt und mit einem Filter entfernt.

Abwärtsmischer werden in Empfängern (Rundfunkempfang, Funktelefon, Satellitenempfänger), die nach dem Superheterodyn-Prinzip arbeiten, sowie in Empfängern von FM-Radar und Geräten zur Geschwindigkeitskontrolle verwendet.

Spiegelfrequenz

Abwärtsmischer mit Spiegelfrequenz

Beim Abwärtsmischer tritt häufig der Fall auf, dass das am HF-Eingang angelegte Signal zusätzlich zu s_HF mit $f_\mathrm{HF} = f_\mathrm{LO} \pm f_\mathrm{ZF}$ ein Spiegelsignal mit der Spiegelfrequenz $f_\mathrm{HF,Sp}=f_\mathrm{LO} \mp f_\mathrm{ZF}$ beinhaltet, welches ebenfalls auf f_ZF herabgesetzt wird. Der Mischer arbeitet in diesem Fall in Gleich- und Kehrlage gleichzeitig.

Deshalb muss der Abwärtsmischer zusätzlich mit einem Spiegelfrequenzfilter am Eingang versehen werden.

Praktische Mischer

Innenschaltung eines symmetrischen Mischers (Gilbertzelle)

Symmetrische Analog-Multiplizierer-Schaltungen zeichnen sich durch besonders wenige und schwache unerwünschte Mischprodukte aus. Trotzdem werden sie für Mischer in der Praxis selten verwendet, da sie wegen der aufwändigen Schaltungstechnik eine höhere Rauschzahl aufweisen – bei sehr schwachen Signalen oft unbrauchbar hoch. Der SO42P ist ein bekannter IC für diese Anwendung.

Meist verwendet man unsymmetrische Schaltungen und nimmt in Kauf, dass neben den gewünschten Summen- und Differenzsignalen auch die ursprünglichen Eingangssignale und eine Vielzahl unerwünschter Kombinationsfrequenzen am Ausgang enthalten sind. Dann muss sichergestellt sein, dass man das Nutzsignal von den weiteren (Stör-)Signalen mit Hilfe von Filtern am Ausgang abtrennen kann. Daraus folgt, dass Übertragungsglieder mit nichtlinearem Verhalten als Mischer benutzt werden können, durch welche die Summe der zu mischenden Signale geschickt wird. In der Praxis bedeutet dies, dass ein „hinreichend schlechter“, also verzerrender Summier-Verstärker als Mischer zu gebrauchen ist. Diese Technik wird als additive Mischung bezeichnet und bildet den mutmaßlichen Ursprung des Begriffs „Mischer“.

Bei Bauteilen wie Dual-Gate-Feldeffekttransistoren oder Mehrgitterröhren führt man die beiden Eingangsspannungen jeweils auf einen separaten Eingang des Steuerelements und spricht dann bereits von multiplikative Mischung. Tatsächlich sind aber die Eingangsspannungen am Ausgang sehr gut nachweisbar, was bei einem Multiplizierer nicht vorkommen darf. Der Anteil unerwünschter Mischprodukte ist geringer als bei einfacheren Schaltungen.

Verwendung eines Rechtecksignales

Das Signal s_LO kann unipolar (0…1) oder bipolar (-1…1) sein.

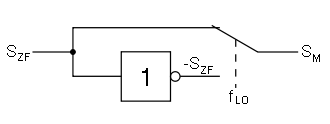
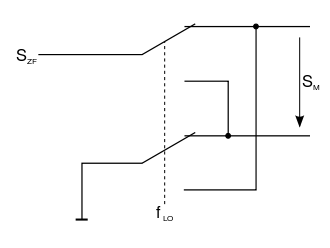
Bipolares Rechteckssignal

Unipolares Rechteckssignal

Ersatzschaltung bei rechteckförmigen Eingangssignal

Bipolar	Unipolar
Mit Logisch-Nicht-Gatter und Wechselschalter	Mit „Einschalter“ (Pull-up)
Mit Kreuzwechselschalter bzw. zwei Wechselschaltern	Mit „Ausschalter“ (Pull-down)

Für Rechteckssignale ergeben sich daraus die Fourierreihen:

$s_\mathrm{LO}(t)= \begin{cases} \frac{1}{2}+\frac{2}{\pi }\sum\limits_{n=0}^{\infty }\frac{\left( -1\right) ^{n}}{2\cdot n+1}\cos \left[ \left( 2n+1\right) \cdot \omega _\mathrm{LO}\cdot t\right] & {\rm unipolar} \\ \frac{4}{\pi }\sum\limits_{n=0}^{\infty }\frac{\left( -1\right) ^{n}}{ 2\cdot n+1}\cos \left[ \left( 2n+1\right) \cdot \omega _\mathrm{LO}\cdot t\right] & {\rm bipolar} \end{cases}$

Es kommen dabei nur ungerade Vielfache der LO-Frequenz vor. Zudem hat das bipolare Rechteckssignal keinen Gleichanteil. Mit dem modulierten ZF-Signal

$s_\mathrm{ZF} = a(t) \cos \left[ \omega _\mathrm{ZF} \cdot t + \varphi (t) \right]$

erhält man am Ausgang eines Multiplizierers mit unipolarem Rechteckssignal:

$s_\mathrm{M}\left( t\right) = {}$	$\frac{a\left( t\right) }{2}\cos \left[ \omega _\mathrm{ZF}\cdot t+\varphi \left( t\right) \right]$
	${} +\frac{a\left( t\right) }{\pi }\left\{ \cos \left[ \left( \omega _\mathrm{LO}+\omega _\mathrm{ZF}\right) \cdot t+\varphi \left( t\right) \right] +\cos \left[ \left( \omega _\mathrm{LO}-\omega _\mathrm{ZF}\right) \cdot t-\varphi \left( t\right) \right] \right\}$
	${} -\frac{a\left( t\right) }{3\cdot \pi }\left\{ \cos \left[ \left( 3\cdot \omega _\mathrm{LO}+\omega _\mathrm{ZF}\right) \cdot t+\varphi \left( t\right) \right] +\cos \left[ \left( 3\cdot \omega _\mathrm{LO}-\omega _\mathrm{ZF}\right) \cdot t-\varphi \left( t\right) \right] \right\}$
	${} + \cdots$

Beim Bipolarsignal entfällt der Anteil der ZF-Frequenz (ω_ZF = 0). Die anderen Anteile haben die doppelte Amplitude [a(t)_bi = 2 a(t)_uni].

Literatur

• Ulrich Tietze, Christoph Schenk, Eberhard Gamm: Halbleiter-Schaltungstechnik. 12. Auflage. Springer, Berlin 2002, ISBN 3-540-42849-6.

Weblinks

• Skript zum Thema Mischer (PDF)