Vertikalkreis

Der Begriff Vertikalkreis wird in der Astronomie für senkrecht stehende Großkreise und zugehörige Messinstrumente verwendet, in der Geodäsie hingegen für die in Theodoliten eingebauten Glaskreise zur Höhenmessung.

Vertikalkreis in der Trigonometrie

Im Sinne der sphärischen Trigonometrie ist ein Vertikalkreis jeder auf den mathematischen Horizont senkrecht stehende Großkreis. Alle diese auch „Vertikal“ genannten Kreise gehen durch den Zenit und Nadir des Beobachtungsortes. Die von diesen Kreisen aufgespannten Ebenen heißen Vertikalebene, sie sind orthogonal zur Horizontebene.

Der durch den West- und Ostpunkt gehende Vertikalkreis heißt „Erster Vertikal“, der durch Nord- und Südpunkt verlaufende „(Himmels-)Meridian“.

Vertikalkreis als Messinstrument

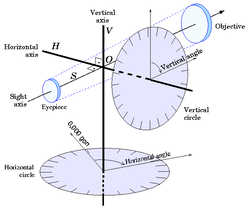
Als Begriff der Instrumentenkunde ist er ein im Aufbau dem Meridiankreis ähnliches, in Höhe und Azimut drehbares astronomisches Winkelmessgerät. Es besteht aus einem Fernrohr (in der Astrogeodäsie vereinzelt auch ein Spiegelobjektiv), zum Beispiel beim „Kern DKM3“), das auf einer horizontalen „Kippachse“ justierbar gelagert ist und von einer stabilen Altazimut-Montierung getragen wird. Die Winkelbewegungen um Kipp- und Stehachse werden mit großen, feingeteilten Kreisen und einem Ablesemikroskop gemessen.

Diese Instrumente stellen die Vorgänger des Theodolits dar und erlauben, Höhen- und Horizontalwinkel von Sternen bzw. von Sternpaaren im horizontalen Koordinatensystem zu bestimmen.

• Ist ein Vertikalkreis zwar schwenkbar oder umlegbar, aber ohne speziellen Horizontalkreis ausgeführt, wird er Durchgangs- oder Passageninstrument genannt. Solche etwa 50 cm hohen, sehr massiv gebauten Instrumente dienen der genauen Zeitbestimmung (siehe auch Sternzeit) und – in internationalen Messkampagnen – der Bestimmung von geografischen Längendifferenzen.
• Ausgestattet mit einem Horrebow-Niveau (einer besonders genauen Libelle) und einem optischen Mikrometer, hat man es bis etwa 1980 für die Horrebow-Talcott-Methode zur Breitenbestimmung eingesetzt (siehe internationaler Breitendienst).

Als eigenständige Instrumententype kam der Vertikalkreis in der Astronomie ab dem 19. Jahrhundert langsam außer Gebrauch, da er puncto Messgenauigkeit dem Passageninstrument und insbesondere dem Meridiankreis unterlegen war. Beispielsweise wurde 1796 ein Vertikalkreis von Carry (London) mit 2 Fuß (61 cm) Brennweite auf der Sternwarte Gotha eingesetzt, aber nach wenigen Jahren weiterverkauft. In der Geodäsie wurde er jedoch - in kompakterer Bauweise - zum Typus des Universalinstruments weiterentwickelt.

Horizontal- und Vertikalkreis eines Theodolits

Geodätische Messeinrichtung

Geodäten verstehen unter dem „Vertikalkreis“ den Vertikal- oder Höhenkreis eines optisch-mechanischen Messinstruments (Theodolit, Tachymeter). Dieser aus Glas oder legiertem Metall bestehende Teilkreis dient der Messung von Zenitwinkeln. Sie können mit Hilfe von Mikrometern oder elektronisch auf etwa 1" genau abgelesen werden, bei größeren Universalinstrumenten sogar auf 0,1".

Der Bezug zur Lotrichtung wird durch einen aufgrund der Schwerkraft sich in Lotrichtung ausrichteten Höhenkompensator oder eine sehr empfindliche Libelle hergestellt; die verbleibende Abweichung heißt Höhenindexfehler.

Zur Erhöhung der Messgenauigkeit wird das Theodolitfernrohr nach der ersten Messung „durchgeschlagen“, das heißt in die zweite Vertikalkreislage gebracht. Die beiden Ablesungen sollten sich auf 360° (beziehungsweise 400 gon) ergänzen. Die allfällige Abweichung hiervon hängt mit dem Kollimations- beziehungsweise Zielachsenfehler zusammen. Durch Messung der Höhenwinkel (Zenitwinkel) in beiden Fernrohrlagen und Differenzbildung der Messwerte entfällt er.

Siehe auch

• Sterndurchgang
• Kippachsenfehler
• Stehachsenfehler
• Achsneigung
• Mayer'sche Formel