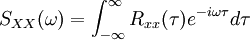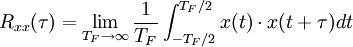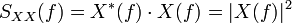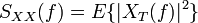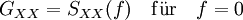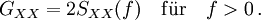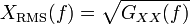Wirkleistungsspektrum

Leistungsdichtespektrum eines Signals

Die spektrale Leistungsdichte, auch Autoleistungsspektrum oder Power-Spektrum-Dichte, gibt die Energie eines Signals in einem infinitesimal kleinen Frequenzband an. Diese Dichte besitzt die Dimension Leistung · Zeit, die Angabe erfolgt meist in den Einheiten Watt/Hertz. Über die Frequenz aufgetragen spricht man vom Leistungsdichtespektrum. Das Integral über alle Frequenzanteile ergibt die komplette Leistung des Signals.

Allgemeines

Der Begriff Spektrum ist nur sinnvoll, wenn das betrachtete Signal, meist handelt es sich um elektrische Signale oder elektromagnetische Strahlung, verschiedene Frequenzen enthält, also nicht monochromatisch beziehungsweise monofrequent ist. Mit Signal ist hierbei sowohl das Nutzsignal als auch der Rauschanteil des Signals gemeint.

Die Kenntnis und Analyse der spektralen Leistungsdichte von Nutzsignal und Rauschen ist wesentlich zur Bestimmung des Signal-Rausch-Verhältnisses und zur Optimierung entsprechender Filter zur Rauschunterdrückung, zum Beispiel im Bildrauschen.

Zur Bestimmung der spektralen Leistungsdichte S_XX(ω) wird oft das Wiener-Chintschin-Theorem herangezogen, wo sie über die Fouriertransformation der zeitlichen Autokorrelationsfunktion des Signals gegeben wird:

$S_{XX}(\omega)=\int_{-\infty}^{\infty} R_{xx}(\tau) e^{-i\omega \tau} d\tau$

Dabei ist

$R_{xx}(\tau) = \lim_{T_F \to \infty} \frac{1}{T_F}\int_{-T_F/2}^{T_F/2} x(t) \cdot x(t + \tau) dt$

die Autokorrelationsfunktion des zeitlichen Signals x(t). Damit ist die spektrale Leistungsdichte auch für Rausch-Signale bestimmbar. In der Praxis werden kaum unendlich lange Zeitreihen vorliegen, deshalb schränkt man das Integrationsintervall ein. Nur für eine stationäre Verteilung ist die Korrelationsfunktion nicht mehr von der Zeit t abhängig.

Autoleistungsspektrum

Das Autoleistungsspektrum, präziser das Autoleistungsdichtespektrum, baut auf den in der Signalanalyse berechneten Fourierspektren X(f) auf und berechnet deren spektrale Leistungsdichte in der Form:

$S_{XX} (f) = X^* (f) \cdot X (f) = | X(f) |^2$

für das (zweiseitige) Eingangsspektrum X(f). Die mit einem Stern versehenen Größe bezeichnet die komplex konjugierte. Sie ist der Spezialfall des Kreuzleistungsspektrums falls beide Signale identisch sind.

Das Autoleistungsdichtespektrum ist gerade, reell und positiv. Dies bedeutet einen Informationsverlust, der eine Umkehrung dieser Prozedur verhindert.

Werden statt der Fouriertransformierten X(f) die über den Zeitraum T gebildeten Kurzzeitspektren X_T(f) verwendet, ergibt sich das Autoleistungsspektrum aus dem Erwartungswert der Spektren:

$\,S_{XX} (f) = E \{ | X_T (f) |^2 \}$

Das Autoleistungsspektrum kann als einseitiges Spektrum G_XX(f) (f 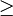$\ge$ 0) dargestellt werden. Es gilt dann:

$G_{XX} = S_{XX} (f) \quad \mathrm{f\ddot ur} \quad f = 0$

und

$G_{XX} = 2 S_{XX} (f) \quad \mathrm{f\ddot ur} \quad f > 0\,.$

Das Autoleistungsspektrum kann für Aussagen über den Frequenzgehalt der analysierten Signale herangezogen werden. Üblicherweise wird hierfür jedoch das sogenannte RMS-Spektrum verwendet, das sich aus dem Autoleistungsspektrum wie folgt ergibt:

$X_\mathrm{RMS} (f) = \sqrt {G_{XX}(f)}$

Beispiele

• Wenn die Korrelationsfunktion eine Delta-Distribution ist, spricht man von weißem Rauschen, in diesem Fall ist S_XX(ω) konstant.
• Für das thermische Rauschen, genauer die spektrale Rauschleistungsdichte, gilt: N₀ =k_B·T. Bei 27 °C beträgt es 4·10^-21 J = 4·10^-21 W/Hz = -204 dBW/Hz
• Im allgemeinen erhält man allerdings für das Leistungsdichtespektrum eine abfallende Funktion. Man unterscheidet verschiedene Arten des Rauschens (z.B. 1/f-Rauschen), je nachdem, wie schnell sie abfällt.
• Wird ein Rauschprozess mit Leistungsdichtespektrum S_XX(ω) über ein lineares, zeitinvariantes System mit Übertragungsfunktion H(ω) übertragen, so ergibt sich am Ausgang ein Leistungsdichtespektrum von 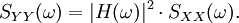$S_{YY}(\omega)= |H(\omega)|^2 \cdot S_{XX}(\omega).$ Die Übertragungsfunktion geht quadratisch in die Formel ein, da das Spektrum eine Leistungsgröße ist.

Siehe auch

• Parsevalsche Gleichung
• Spektrale Beschleunigungsdichte

Literatur

• Hans Dieter Lüke: Signalübertragung. 6. Auflage. Springer, 1995, ISBN 3-540-58753-5.