Würfelverdoppelung

Verhältnis von Volumen zur Kantenlänge eines Würfels

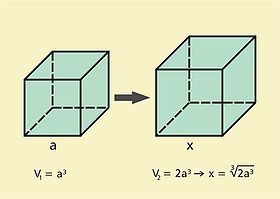
Die Würfelverdoppelung (Würfelvolumenverdoppelung) (auch Delisches Problem genannt) gehört zu den klassischen Problemen der antiken Mathematik.

Nach einer Legende befragten die Bewohner der Insel Delos während einer Pestepidemie 430 v. Chr. das Orakel von Delphi um Rat. Dort wurden sie aufgefordert, den würfelförmigen Altar im Tempel des Apollon im Volumen zu verdoppeln. Für antike Mathematiker bedeutete dies, dass die Seitenlänge eines Würfels mit dem doppelten Volumen unter ausschließlicher Verwendung von Zirkel und Lineal konstruiert werden sollte.

Erst im 19. Jahrhundert wurde bewiesen, dass diese Aufgabe unlösbar ist. Der Beweis verwendet die Galoistheorie (Évariste Galois, französischer Mathematiker) und läuft im Kern darauf hinaus, dass die irrationale Zahl $\sqrt[3]{2}$ nicht durch ganze Zahlen, die vier Grundrechenarten und Quadratwurzeln ausgedrückt werden kann.