- Zweiwertige Logik
-
Dieser Artikel schildert die moderne Verwendung der Bezeichnung „klassische Logik“. Für Informationen über Logik in der klassischen Antike und über traditionelle Logik im weiteren Sinn siehe Logik, Syllogistik und Begriffslogik. - Jede Aussage hat einen von genau zwei Wahrheitswerten, meist falsch und wahr (Prinzip der Zweiwertigkeit/Bivalenzprinzip).
- Der Wahrheitswert jeder zusammengesetzten Aussage ist eindeutig durch die Wahrheitswerte ihrer Teilaussagen bestimmt (Prinzip der Extensionalität).
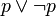(z. B. „Es regnet, oder es ist nicht der Fall, dass es regnet.“)- Satz vom ausgeschlossenen Widerspruch
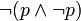(z. B. „Es ist nicht der Fall, dass es (zugleich und am selben Ort) regnet und nicht regnet.“)- Satz vom ausgeschlossenen Dritten
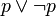- (z. B. „Die Erde ist rund, oder es ist nicht der Fall, dass die Erde rund ist.“)
- Verum sequitur ex quodlibet
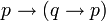(z. B. „Wenn es regnet, dann regnet es (auch) unter der Voraussetzung, dass die Erde eine Scheibe ist.“)- Ex falso sequitur quodlibet
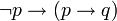(z. B. „Wenn es nicht regnet, dann ist unter der Voraussetzung, dass es (am selben Ort und zur selben Zeit) regnet, die Erde eine Scheibe.“)- Paradox der materialen Implikation
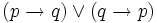(Von zwei beliebigen Sätzen ist immer mindestens einer die hinreichende Bedingung für den jeweils anderen.)- Antoine Arnauld, Pierre Nicole: Die Logik oder die Kunst des Denkens. 2., durchgesehene und um eine Einleitung erweiterte Auflage. Darmstadt 1994, ISBN 3-534-03710-3.
- Dov Gabbay: Classical vs non-classical logic. In: D. M. Gabbay, C.J. Hogger, J.A. Robinson (Hrsg.): Handbook of Logic in Artificial Intelligence and Logic Programming. Oxford University Press, 1994, Band 2, Kapitel 2.6.
- Jan Łukasiewicz: O zasadzie wyłączonego środka. (deutsch: Über den Satz vom ausgeschlossenen Dritten) In: Przeglad Filozoficzny. 13 (1910), 372–373.
- Jan Łukasiewicz: Z historii logiki zdan. In: Przegl. filoz. 37 (1934), 417–437. (Entdeckung der stoischen Junktorenlogik.)
- Jan Łukasiewicz: Zur Geschichte der Aussagenlogik. In: Erkenntnis 5 (1935) 111–131. (Deutsche Übersetzung des Artikels Z historii logiki zdan.)
- Gottlob Frege: Begriffsschrift, eine der arithmetischen nachgebildete Formelsprache des reinen Denkens. Halle 1879.
- L. Kreiser, S. Gottwald, W. Stelzner (Hrsg.): Nichtklassische Logik. Eine Einführung. Akademie-Verlag, Berlin 21990, ISBN 3-05-000274-3.
- Stewart Shapiro: „Classical Logic“ in der Stanford Encyclopedia of Philosophy (englisch, inklusive Literaturangaben)
Unter der klassischen Logik versteht man ein logisches System, das die Aussagen-, die Prädikatenlogik erster oder höherer Stufe sowie im Allgemeinen den Identitätsbegriff enthält. Eine erste Axiomatisierung eines solchen Systems hat Gottlob Frege in seiner Begriffsschrift (1879) entwickelt.
Die klassische Logik ist durch genau zwei Eigenschaften gekennzeichnet:
Das Prinzip der Zweiwertigkeit ist vom Satz vom ausgeschlossenen Dritten zu unterscheiden:
stellt einen Satz der klassischen Aussagenlogik dar, kann also syntaktisch aus den Regeln und Axiomen des logischen Systems hergeleitet werden, ohne dass der Wahrheitsbegriff explizit eine Rolle spielt. Demgegenüber ist das Prinzip der Zweiwertigkeit eine Aussage über die Semantik der Logik, welche jeder Aussage einen Wahrheitswert zuordnet.
In Abgrenzung zur klassischen Logik entstehen nichtklassische Logiksysteme, wenn man das Prinzip der Zweiwertigkeit, das Prinzip der Extensionalität oder sogar beide Prinzipien aufhebt. Nichtklassische Logiken, die durch die Aufhebung des Prinzips der Zweiwertigkeit entstehen, sind Mehrwertige Logiken. Die Zahl der Wahrheitswerte (vielleicht besser: Pseudowahrheitswerte) kann dabei endlich sein (z. B. dreiwertige Logik), ist aber oft auch unendlich (z. B. Fuzzy-Logik). Logiken, die durch die Aufhebung der Extensionalität entstehen, verwenden hingegen Junktoren (Konnektive), bei denen sich der Wahrheitswert des zusammengesetzten Satzes nicht mehr eindeutig aus dem Wahrheitswert seiner Teile bestimmen lässt. Ein Beispiel für nichtextensionale Logik ist die Modallogik, die die einstelligen nichtextensionalen Operatoren „es ist notwendig, dass“ und „es ist möglich, dass“ einführt. Ein anderes Beispiel ist die intuitionistische Logik, die zwar keine neuen Operatoren einführt, aber die bestehenden Operatoren anders interpretiert.
Die algebraische Struktur der klassischen Aussagenlogik ist eine zweielementige Boolesche Algebra. Die formale zweiwertige Logik im modernen Sinn wurde In der zweiten Hälfte des 19. Jahrhunderts von Boole, Frege und anderen entwickelt. Die Bezeichnung „klassische Logik“ entstand dann im 20. Jahrhundert zur Abgrenzung von einer Reihe anderer, als nicht-klassisch bezeichneter Logiken.
Manchmal wird der Begriff klassische Logik auch als historischer Begriff verwendet, d. h. bezogen auf Logiker der Antike. Nun wurde aber in der Antike durchaus nicht nur klassische Logik betrieben; vielmehr behandelte schon Aristoteles, der in historischem Sinn geradezu mustergültig klassische Logiker, Sachverhalte nichtklassischer Logik. Es ist – je nach Zusammenhang – nicht immer ganz leicht zu erkennen, in welchem Sinn ein Sprecher/eine Sprecherin den Begriff „klassische Logik“ verwendet.
Beispiele klassisch gültiger Aussagen
Einige bekannte Aussagen, die in der klassischen Logik gültig sind, sind folgende:
Literatur
Weblinks
Wikimedia Foundation.
