Aristotelische Logik

Gregor Reisch, „Die Logik präsentiert ihre zentralen Themen“, Margarita Philosophica, 1503/08 (?). Die beiden Hunde veritas und falsitas jagen den Hasen problema, die Logik eilt mit dem Schwert syllogismus bewaffnet hinterher. Links unten Parmenides, mit dem die logische Argumentation Einzug in die Philosophie hielt, in einer Höhle.

Logik (griechisch ἡ λογική (τέχνη) he logiké téchne „die denkende [Kunst, Vorgehensweise]“) ist die Lehre des vernünftigen (Schluss-)Folgerns. Die Logik untersucht die Gültigkeit von Argumenten hinsichtlich ihrer Struktur unabhängig vom konkreten Inhalt der eigentlichen Aussagen. In diesem Sinne spricht man auch von „formaler“ Logik. Die Logik ist sowohl ein Teilgebiet der Philosophie als auch der Mathematik und der Informatik.

Seit dem 20. Jahrhundert versteht man unter Logik überwiegend symbolische Logik. Diese baut auf einer künstlichen Sprache auf und verwendet streng definierte Schlussregeln. Ein einfaches Beispiel für ein solches formales System ist die Aussagenlogik. Die symbolische Logik nennt man auch mathematische Logik oder formale Logik im engeren Sinn. Die Logik hatte nicht immer eine in diesem Sinn formale Struktur, sondern befasste sich in der Antike und im Mittelalter überwiegend mit natürlichsprachlichen Argumenten.

Unterschiedliche Bedeutungen des Begriffs „Logik“

Der Ausdruck „Logik“, im Griechischen he logike techne, „steht sowohl in der älteren Stoa wie im älteren Peripatos für eine Lehre vom Argumentieren bzw. Schließen, ist in dieser Bedeutung jedoch nicht vor dem 1. Jh. v. Chr. belegt“.^[1] Der Begriff wurde bereits von dem antiken Stoiker Zenon von Kition geprägt.

Im Deutschen wird das Wort „Logik“ im 19. Jh. vielfach (etwa bei Immanuel Kant oder Georg Wilhelm Friedrich Hegel) auch im Sinne einer Erkenntnistheorie, Ontologie oder einer allgemeinen Dialektik verwendet. Die Logik im modernen Sinne wurde auf der anderen Seite häufig anders bezeichnet, etwa als Analytik, Dialektik oder Logistik. Auch heute noch sind in verschiedenen Disziplinen Wendungen wie Logik der Dichtung u.ä. verbreitet, bei denen unter „Logik“ keine Theorie des Folgerns verstanden wird, sondern eine Lehre allgemeiner „Gesetze“ oder Verfahrensweisen, die in einem bestimmten Bereich gelten.

Insbesondere in der Tradition der Philosophie der normalen Sprache wurde unter einer „logischen“ Analyse vielfach eine Analyse begrifflicher Zusammenhänge verstanden.

Die einleitend dargestellte Verwendungsweise des Ausdrucks „Logik“ ist dagegen seit Beginn des 20. Jahrhunderts üblich.

In der Umgangssprache werden Ausdrücke wie „Logik“ oder „logisches Denken“ darüber hinaus in einem sehr viel weiteren oder völlig anderen Sinne verstanden und etwa einem „lateralen Denken“ gegenübergestellt. Ebenso gibt es den Begriff der „Frauenlogik“, „Männerlogik“, der „Affektlogik“ und den Begriff der „Alltagslogik“ – bekannt auch als „gesunder Menschenverstand“ (common sense) – in der Umgangssprache. In diesen Bereichen bezieht sich „Logik“ oft auf Formen des Handelns, der Pragmatik. Ein Argument wird umgangssprachlich als „logisch“ bezeichnet, wenn dieses stichhaltig, zwingend, überzeugend, einleuchtend und klar ist. In einem logischen Argument soll die Fertigkeit des Denkens zum Ausdruck kommen.

Auch in gegenwärtigen Debatten ist weithin unbestritten, dass die Theorie des korrekten Folgerns den Kern der Logik ausmacht; umstritten ist jedoch, welche Theorien genau noch zur Logik zu rechnen sind und welche nicht. Strittige Fälle sind etwa die Mengentheorie, die Argumentationstheorie (die sich etwa unter pragmatischer Rücksicht mit Fehlschlüssen beschäftigt) und die Sprechakttheorie.

Geschichte der Logik

Antike

Als Begründer der Logik gilt der antike griechische Philosoph Aristoteles. Er diskutiert in verschiedenen Schriften seines Organon Themen wie Begriff, Aussage, Definition, Beweis und Fehlschluss. In seinem logischen Hauptwerk, der Ersten Analytik, entwickelt er die Syllogistik, ein formales logisches System im modernen Sinn, in dem Argumente starrer Struktur, Syllogismen genannt, untersucht werden. In einem Syllogismus wird aus zwei Aussagen auf eine dritte Aussage geschlossen. Diese Aussagen setzen ihrerseits auf bestimmte Weise Begriffe zueinander in Beziehung; zum Beispiel wird mit Formulierungen wie „P kommt allem S zu“ oder „P wird über alles S ausgesagt“ ausgedrückt, dass alles, was unter den Begriff S fällt, auch unter den Begriff P fällt – in der Sprechweise der mittelalterlichen Syllogistik: „Alles S ist P“. Ein Beispiel für einen gültigen Syllogismus ist das Argument „Kein Rechteck ist ein Kreis. Alle Quadrate sind Rechtecke. Also ist kein Quadrat ein Kreis“. Logische Systeme, in deren Aussagen Begriffe zueinander in Beziehung gesetzt werden, heißen Begriffslogiken.

Gleichfalls auf Aristoteles zurück geht die bereits in seiner Metaphysik entwickelte Lehre von einigen fundamentalen Grundsätzen menschlichen Denkens. Hierzu zählen der Satz vom Widerspruch und der Satz vom ausgeschlossenen Dritten, die in der modernen Logik zwar keine metaphysische Rolle mehr spielen, als logische Gesetze aber innerhalb der klassischen Logik und auch in manchen nichtklassischen Logiken gelten.

Beim Umgang mit Syllogismen bedient sich Aristoteles heute noch verwendeter Methoden, so führt er indirekte Beweise und widerlegt ungültige Syllogismen auf semantische Weise, indem er Gegenbeispiele angibt. Schließlich skizziert er eine modallogische Erweiterung seiner Syllogistik mit den logischen Operatoren „notwendig“, „möglich“, „unmöglich“ und „kontingent“. Viele seiner logischen Grundsätze formuliert Aristoteles als Syllogismen, darunter die Transitivität: „Ist A jedem B eigen und B jedem C eigen, so ist A jedem C eigen“ (Modus Barbara).

Unabhängig von der aristotelischen Logik entwickelt sich im Jahrhundert nach Aristoteles in der megarischen und stoischen Philosophenschule die zweiwertige Aussagenlogik. Eines der wenigen erhaltenen Fragmente über die megarische Logik schreibt Philon von Megara die älteste Wahrheitstafel zum Konditional zu. Seine Methode führt vor allem der Stoiker Chrysipp weiter; er entwickelt die erste bekannte axiomatische Aussagenlogik mit Junktoren in Kalkülform und prägt die spätere stoische Logik. Sie geht allerdings nach der Antike bis auf Bruchstücke verloren und hat kaum eine historische Wirkung im Vergleich zur aristotelischen Logik. Erst Arbeiten von Łukasiewicz und Mates bringen sie neu ins Bewusstsein.

Mittelalter

Eine weitere bedeutende Epoche für die Logik ist das Mittelalter. Im mittelalterlichen Universitätsbetrieb hat die Logik als eine der septem artes liberales ihren Platz in der sogenannten „Artistenfakultät“ (facultas artium). Das Studium der artes ist Voraussetzung für das Studium an allen anderen Fakultäten. Ab etwa der Mitte des 13. Jahrhunderts umfasst der Unterrichtsstoff der Logik drei separate Textkorpora. Bei der logica vetus und der logica nova handelt es sich um überlieferte logische Schriften, insbesondere das Organon des Aristoteles und die Kommentare des Boëthius und des Porphyrius. Die parva logicalia kann man als Eigenschöpfung der mittelalterlichen Logik ansehen. Hier werden abseits der antiken Vorlagen eine ganze Reihe von neuen Problemstellungen aus dem Grenzbereich zwischen Logik und Semantik entwickelt und in voneinander unabhängigen Traktaten diskutiert. Einige gängige Traktattypen seien kurz vorgestellt:

• De proprietatibus terminorum befasst sich mit den Eigenschaften der materialen (nicht-logischen) Termini.
• De syncategorematicis untersucht dagegen die formalen, d.h. logischen Ausdrücke.
• De suppositio terminorum formuliert die mittelalterliche Suppositionstheorie
• Bei De consequentiis geht es um Folgerungen.
• De insolubilibus hat Paradoxien und Trugschlüsse zum Gegenstand.
• De Relativis befasst sich mit den Eigenschaften anaphorischer Ausdrücke.
• De Modalibus untersucht Modal-Ausdrücke.
• Bei De Obligationibus geht es um die logischen Bedingungen eines kohärenten Disputs.

Bedeutende mittelalterliche Logiker waren Petrus Abaelardus, William of Sherwood, Petrus Hispanus, Wilhelm von Ockham und Johannes Buridan.

Neuzeit

In der Neuzeit erlahmt zunächst das Interesse an der Logik. Weit verbreitet ist die Ansicht Immanuel Kants, dass das System der Logik mit der Aristotelischen Syllogistik zum Abschluss gekommen wäre, und dass es hier deshalb nichts weiter zu entdecken gäbe. Vielfach erschöpft sich daher die Behandlung des Gegenstandsbereich der Logik in der Vermittlung von Lehrbuchwissen. Ausnahmen sind beispielsweise Gottfried Wilhelm Leibniz oder Gottfried Ploucquet.

Erst Mitte des neunzehnten Jahrhunderts findet die Logik wieder breitere Beachtung, zunächst vor allem in England. Richtungsweisend ist hier George Boole mit dem kürzeren Traktat „The Mathematical Analysis of Logic“ (1847) und seinem späteren Hauptwerk „Laws of Thought“ (1854). Booles Idee ist es, Logik als einen mathematischen Kalkül aufzufassen, das auf die Werte 1 und 0 (wahr und falsch) beschränkt ist. Auf Klassensymbolen können so algebraische Operationen wie Addition, Multiplikation usw. ausgeführt werden. Auf diese Weise entwickelt Boole ein vollständiges System der einstelligen Prädikatenlogik, welches die Syllogistik als Subsystem enthält. Zeitgleich mit Boole veröffentlicht Augustus De Morgan sein Werk „Formal Logic“ 1847. De Morgan interessiert sich hier u.a. für eine Verallgemeinerung der Syllogistik auf Aussagen der Form „Die meisten A sind B“. Ein weiterer Logiker in England ist John Venn, der sein Buch „Symbolic Logic“ mit den berühmten Venn-Diagrammen 1881 veröffentlicht. An der logischen Forschung sind außerdem in Amerika Charles Sanders Peirce und in Deutschland Ernst Schröder beteiligt.

Der eigentliche Durchbruch zur modernen Logik gelingt jedoch Gottlob Frege, der wohl als der neben Aristoteles bedeutendste Logiker überhaupt angesehen werden muss. In seiner Begriffsschrift (1879) stellt er zum ersten Mal eine volle Prädikatenlogik zweiter Stufe vor. Außerdem entwickelt er hier die Idee einer formalen Sprache und darauf aufbauend die Idee des formalen Beweises, in dem nach Freges Worten nichts „dem Errathen überlassen“ bleibt. Gerade diese Ideen bilden eine ganz wesentliche theoretische Grundlage für die Entwicklung der modernen Computertechnik und Informatik. Freges Werk wird allerdings von seinen Zeitgenossen zunächst kaum wahrgenommen; dies mag u.a. an seiner sehr schwer zu lesenden logischen Notation liegen. In den beiden 1893 und 1903 erschienenen Bänden der „Grundgesetze der Arithmetik“ versucht Frege, die gesamte Mathematik in einer Art Mengentheorie zu axiomatisieren. Dieses System enthält jedoch einen Widerspruch (die sogenannte Russellsche Antinomie), wie Frege in einem berühmt gewordenen Brief von Bertrand Russell aus dem Jahr 1902 erfahren muss.

Russell selbst bleibt es vorbehalten, zusammen mit Alfred North Whitehead in den Principia Mathematica (1910) die erste widerspruchsfreie mengentheoretische Grundlegung der Mathematik vorzulegen. Die Autoren würdigen Frege im Vorwort, ihm verdankten sie das meiste in „logisch-analytischen Fragen“. Im Gegensatz zu Freges Werk werden die Principia Mathematica ein durchschlagender Erfolg. Einen Grund hierfür kann man u.a. in der von Russell/Whitehead verwendeten Notation sehen, die zu weiten Teilen heute noch üblich ist. Anstöße zu dieser Notation lieferte Giuseppe Peano, ein weiterer bedeutender Logiker des ausgehenden 19. Jahrhunderts, den Russell im Jahre 1900 bei einem Kongress kennen lernte. Neben seinen Gedanken zur logischen Notation ist Peano vor allem für seine Axiomatisierung der Zahlentheorie (die sogenannten Peano-Axiome) bekannt.

Moderne

Das aussagenlogische Fragment der „Principia Mathematica“ dient als Ausgangspunkt für die Entwicklung einer ganzen Reihe metalogischer Begriffe. In seiner Habilitationsschrift von 1918 zeigt Paul Bernays (aufbauend auf der Arbeit David Hilberts) Widerspruchsfreiheit, syntaktische und semantische Vollständigkeit und Entscheidbarkeit und untersucht die Unabhängigkeit der Axiome (wobei er feststellt, dass eines der Axiome tatsächlich abhängig, also überflüssig, ist).

Neben der axiomatischen Methode der „Principia“ werden weitere Kalkültypen entwickelt. 1934 präsentiert Gerhard Gentzen sein System des natürlichen Schließens und den Sequenzenkalkül. Hierauf aufbauend entwickelt Evert Willem Beth 1959 den Tableaukalkül. Wiederum an diesem orientiert sich Paul Lorenzen bei seiner Dialogischen Logik.

Die moderne Logik bringt außerdem die Entwicklung einer Semantik der Prädikatenlogik mit sich. Eine wichtige Vorarbeit hierzu stellt das berühmte Löwenheim-Skolem-Theorem dar (zuerst bewiesen von Leopold Löwenheim im Jahr 1915, ein allgemeineres Resultat zeigt Albert Thoralf Skolem 1920). Kurt Gödel beweist 1929 die Vollständigkeit der Prädikatenlogik erster Stufe (Gödelscher Vollständigkeitssatz), 1930 die Unvollständigkeit der Peano-Arithmetik (Gödelscher Unvollständigkeitssatz). 1933 formuliert Alfred Tarski eine Wahrheitstheorie für die Prädikatenlogik.

Weitere wichtige Ereignisse in der Geschichte der modernen Logik sind die Entwicklung der Intuitionistischen Logik, der Modallogik, des Lambda-Kalküls, der Typentheorie sowie der Stufenlogik (Logik höherer Stufe). Ein wichtiger Trend in der modernen Logik ist auch die Entwicklung von Theorembeweisern (siehe auch Künstliche Intelligenz) sowie die Anwendung von Logik in der Informatik durch Formale Methoden.

Teilgebiete

Klassische Logik

Hauptartikel: Klassische Logik

Von klassischer Logik bzw. von einem klassischen logischen System spricht man genau dann, wenn folgende semantische Bedingungen erfüllt sind:

1. Jede Aussage hat genau einen von genau zwei Wahrheitswerten, die meist als wahr und falsch bezeichnet werden. Man nennt dieses Prinzip das Prinzip der Zweiwertigkeit oder Bivalenzprinzip.
2. Der Wahrheitswert einer zusammengesetzten Aussage ist eindeutig durch die Wahrheitswerte ihrer Teilaussagen und die Art, wie diese zusammengesetzt sind, bestimmt. Dieses Prinzip heißt das Prinzip der Extensionalität oder der Kompositionalität.

Der Begriff klassische Logik ist mehr im Sinn von etablierter, grundlegender Logik zu verstehen, weil die nichtklassischen Logiken auf sie aufbauen, denn als historischer Verweis. Vielmehr war es so, dass bereits Aristoteles, sozusagen der klassische Vertreter der Logik, sich sehr wohl mit mehrwertiger Logik, also nichtklassischer Logik beschäftigt hat.

Die wichtigsten Teilgebiete der formalen klassischen Logik sind die klassische Aussagenlogik, die Prädikatenlogik der ersten Stufe und Logik höherer Stufe, wie sie am Ende des 19. und am Anfang des 20. Jahrhunderts durch Gottlob Frege, Charles Sanders Peirce, Bertrand Russell und Alfred North Whitehead entwickelt wurden. In der Aussagenlogik werden Aussagen daraufhin untersucht, ob sie ihrerseits wieder aus Aussagen zusammengesetzt sind, die durch Junktoren (z. B. „und“, „oder“) miteinander verbunden sind. Besteht eine Aussage nicht aus durch Junktoren verbundenen Teilaussagen, dann ist sie aus Sicht der Aussagenlogik atomar, d. h. nicht weiter zerlegbar.

In der Prädikatenlogik lässt sich auch die innere Struktur von Sätzen darstellen, die aussagenlogisch nicht weiter zerlegbar sind. Dargestellt wird die innere Struktur der Aussagen dabei durch Prädikate (auch Aussagefunktionen genannt) einerseits und durch deren Argumente andererseits; dabei drückt das Prädikat zum Beispiel eine Eigenschaft aus, die auf sein Argument zutrifft, oder eine Relation, die zwischen seinen Argumenten besteht. Der Begriff der Aussagefunktion ist aus dem mathematischen Begriff der Funktion abgeleitet. Eine logische Aussagenfunktion hat genau wie eine mathematische Funktion einen Wert, der aber kein numerischer, sondern ein Wahrheitswert ist.

Der Unterschied zwischen Prädikatenlogik der ersten Stufe und Prädikatenlogik höherer Stufe besteht darin, worüber mittels der Quantoren („alle“, „mindestens ein“) quantifiziert wird: In der Prädikatenlogik erster Stufe wird nur über Individuen quantifiziert (z. B. „Alle Schweine sind rosa“), in der Prädikatenlogik höherer Stufe wird auch über Prädikate selbst quantifiziert (z. B. „Es gibt ein Prädikat, das auf Sokrates zutrifft“).

Formal bedarf die Prädikatenlogik einer Unterscheidung zwischen verschiedenen Ausdruckskategorien wie Termen, Funktoren, Prädikatoren und Quantoren. Diese wird in der Stufenlogik, einer Form des typisierten Lambda-Kalküls, überwunden. Dadurch wird zum Beispiel die mathematische Induktion eine gewöhnliche, ableitbare Formel.

Die bis zum 19. Jahrhundert dominante Syllogistik, die auf Aristoteles zurückgeht, lässt sich als ein Vorläufer der Prädikatenlogik verstehen. Ein Grundbegriff der Syllogistik ist der Begriff „Begriffe“; er wird dort nicht weiter zerlegt. In der Prädikatenlogik werden Begriffe als einstellige Prädikate ausgedrückt; mit mehrstelligen Prädikaten lässt sich zusätzlich die innere Struktur von Begriffen analysieren und damit die Gültigkeit von Argumenten zeigen, die syllogistisch nicht fassbar sind. Ein häufig zitiertes intuitiv eingängiges Beispiel ist das Argument „Alle Pferde sind Tiere; also sind alle Pferdeköpfe Tierköpfe“, das sich erst in höheren Logiken wie der Prädikatenlogik herleiten lässt.

Es ist technisch möglich, die formale Syllogistik des Aristoteles so zu erweitern und zu verändern, dass der Prädikatenlogik gleichmächtige Kalküle entstehen. Solche Unternehmungen sind im 20. Jahrhundert vereinzelt von philosophischer Seite her vorgenommen worden und sind philosophisch motiviert, zum Beispiel aus dem Wunsch heraus, auch rein formal Begriffe als elementare Bestandteile von Aussagen ansehen zu können und sie nicht prädikatenlogisch zerlegen zu müssen. Mehr zu solchen Kalkülen und den philosophischen Hintergründen findet sich im Artikel zur Begriffslogik.

Kalkültypen und logische Verfahren

Die moderne formale Logik widmet sich der Aufgabe, exakte Kriterien für die Gültigkeit von Schlüssen und die logische Gültigkeit von Aussagen (semantisch gültige Aussagen heißen Tautologien, syntaktisch gültige Aussagen Theoreme) zu entwickeln. Hierzu wurden verschiedene Verfahren entwickelt.

Insbesondere im Bereich der Aussagenlogik (aber nicht nur) sind semantische Verfahren gebräuchlich, also solche Verfahren, die darauf beruhen, dass den Aussagen ein Wahrheitswert zugeschrieben wird. Hierzu zählen einerseits:

• Wahrheitstabellen

Während Wahrheitstabellen eine vollständige Auflistung aller Wahrheitswertkombinationen vornehmen (und insofern auch nur im aussagenlogischen Bereich verwendbar sind), gehen die übrigen (auch prädikatenlogisch verwertbaren) Verfahren nach dem Schema einer Reductio ad absurdum vor: Wenn eine Tautologie bewiesen werden soll, geht man von ihrer Negation aus und versucht einen Widerspruch abzuleiten. Hier sind drei Varianten gebräuchlich:

• Resolution,
• Semantische Bäume und
• Beth-Tableaux (nach: Evert Willem Beth)

Zu den logischen Kalkülen, die ohne semantische Bewertungen auskommen, zählen:

• Axiomatische Logikkalküle
• Systeme natürlichen Schließens
• Sequenzenkalküle
• Dialogische Logiken

Nichtklassische Logiken

Von nichtklassischer Logik bzw. einem nichtklassischen logischen System spricht man, wenn mindestens eines der beiden oben genannten klassischen Prinzipien (Zweiwertigkeit und/oder Extensionalität) aufgegeben wird. Wird das Prinzip der Zweiwertigkeit aufgegeben, entsteht mehrwertige Logik. Wird das Prinzip der Extensionalität aufgegeben, entsteht intensionale Logik. Intensional sind zum Beispiel die Modallogik und die intuitionistische Logik. Werden beide Prinzipien aufgegeben, entsteht mehrwertige intensionale Logik.

Philosophische Logiken

Philosophische Logik ist ein unscharfer Sammelbegriff für verschiedene formale Logiken, die die klassische Aussagen- und Prädikatenlogik in unterschiedlicher Weise verändern beziehungsweise erweitern, in der Regel indem sie deren Sprache um weitere Operatoren für bestimmte Redebereiche anreichern. Philosophische Logiken sind meist nicht von direktem Interesse für die Mathematik, finden aber Anwendung zum Beispiel in der Sprachwissenschaft oder Informatik. Sie behandeln vielfach Fragestellungen, die weit in die Geschichte der Philosophie zurückreichen und teilweise schon seit Aristoteles diskutiert werden, zum Beispiel den Umgang mit Modalitäten (Möglichkeit und Notwendigkeit).

Der philosophischen Logik zugerechnet werden unter anderem folgende Gebiete:

• Modallogik führt modale Satzoperatoren wie „es ist möglich, dass...“ oder „es ist notwendig, dass...“ ein und untersucht die Gültigkeitsbedingungen modaler Argumente;
• epistemische Logik bzw. doxastische Logik untersucht und formalisiert Aussagen des Glaubens, der Überzeugung und des Wissens sowie aus ihnen gebildete Argumente;
• Deontische Logik oder Normenlogik untersucht und formalisiert Gebote, Verbote und Zugeständnisse („es ist erlaubt, dass...“) sowie aus ihnen gebildete Argumente;
• Temporale Logik der Aktionen, die Quantenlogik und andere temporale Logiken untersuchen und formalisieren Aussagen und Argumente, in denen Bezug auf Zeitpunkte oder Zeitabschnitte genommen wird;
• Interrogativlogik untersucht Fragesätze sowie die Frage, ob sich zwischen Fragesätzen logische Beziehungen herstellen lassen;
• Konditionalsatzlogik untersucht über die materiale Implikation hinausgehenden „Wenn–dann“-Bedingungen;
• Relevanzlogik verwendet anstelle der materialen Implikation eine Implikation, die nur dann wahr ist, wenn ihr Vordersatz für ihren Nachsatz relevant ist (siehe auch das nachfolgende Kapitel)
• Die metakonsistente Logik hat eine alternative Art mit Kontradiktionen umzugehen.

Intuitionismus, Relevanzlogik und konnexe Logik

Die meistdiskutierten Abweichungen von der klassischen Logik stellen solche Logiken dar, die auf bestimmte Axiome der klassischen Logik verzichten. Die im engeren Sinne nicht-klassischen Logiken sind „schwächer“ als die klassische Logik, d.h. in diesen Logiken sind weniger Argumente gültig als in der klassischen Logik, es sind aber alle dort gültigen Argumente auch klassisch gültig.

Hierzu gehören die von L. E. J. Brouwer entwickelte Intuitionistische Logik, welche das „duplex-negatio“-Axiom (aus der doppelten Negation einer Aussage p folgt p)

(DN) $\neg\neg p \Rightarrow p$

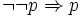
nicht enthält, woraufhin der Satz „tertium non datur“ (für jede Aussage p gilt: p oder nicht-p),

(TND) $\neg p \or p$

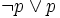
nicht mehr ableitbar ist, der Minimalkalkül I. Johanssons, womit der Satz „ex falso quodlibet“ (aus einem Widerspruch folgt eine beliebige Aussage),

(EFQ) $\neg p \Rightarrow (p \Rightarrow q)$

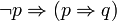
nicht mehr abgeleitet werden kann, sowie die sich hieran anschließenden Relevanzlogiken, in welchen nur solche Implikationen gültig sind, in denen das Antezedens für das Sukzedens relevant ist. In der Dialogischen Logik und in den Sequenzenkalkülen sind sowohl die Klassischen als auch die nicht-klassischen Logiken durch entsprechende Zusatzregeln ineinander überführbar.

Auf der anderen Seite sind Logiken zu erwähnen, die Prinzipien enthalten, die klassisch nicht gültig sind. So gilt etwa in einer konnexen Logik 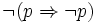$\neg (p \Rightarrow \neg p)$ – ein Satz, der trotz seiner hohen Plausibilität keine klassische Tautologie darstellt. Insofern die klassische Logik maximal-konsistent ist, d.h. insofern jede echte Verstärkung eines klassischen Kalküls zu einem Widerspruch führen wurde, könnte dieser Satz nicht etwa einem klassischen Kalkül als weiteres Axiom hinzugefügt werden; vielmehr müsste ein klassischer Kalkül zunächst schwächer gemacht werden.

• Connexive Logic. Eintrag in der Stanford Encyclopedia of Philosophy (englisch, inklusive Literaturangaben)Vorlage:SEP/Wartung/Parameter 1 und weder Parameter 2 noch Parameter 3

Mehrwertige und Fuzzy-Logik

Hauptartikel: Mehrwertige Logik

Quer hierzu stehen die mehrwertigen Logiken, in denen das Prinzip der Zweiwertigkeit und oft auch der aristotelische Satz vom ausgeschlossenen Dritten nicht gelten, darunter die dreiwertige und die unendlichwertige Logik von Jan Łukasiewicz („Warschauer Schule“). Zahlreiche Anwendungen in der Steuerungstechnik findet die unendlichwertige Fuzzy-Logik, während etwa die endlichwertige Logik von Gotthard Günther („Günther-Logik“) auf Probleme der sich selbst erfüllende Voraussagen in der Soziologie angewandt wurde.

Nichtmonotone Logiken

Man nennt ein logisches System monoton, wenn jedes gültige Argument auch dann gültig bleibt, wenn man zusätzliche Prämissen hinzufügt: Was einmal bewiesen wurde, bleibt in einer monotonen Logik immer gültig, also auch dann, wenn man zu einem späteren Zeitpunkt über neue Informationen verfügt. Sehr viele logische Systeme haben diese Monotonie-Eigenschaft, darunter alle klassischen Logiken wie die Aussagen- und die Prädikatenlogik.

Im alltäglichen und auch wissenschaftlichen Schließen werden jedoch oft vorläufige Schlussfolgerungen gezogen, die im streng logischen Sinn nicht gültig sind und die unter Umständen zu einem späteren Zeitpunkt revidiert werden müssen. Zum Beispiel ließe sich aus den Aussagen „Tux ist ein Vogel.“ und „Die meisten Vögel können fliegen.“ vorläufig darauf schließen, dass Tux fliegen kann. Wenn wir nun aber die zusätzliche Information „Tux ist ein Pinguin.“ erhalten, dann müssen wir diesen Schluss korrigieren, denn Pinguine sind nicht flugfähige Vögel. Um diese Art des Schließens abzubilden, wurden nichtmonotone Logiken entwickelt: Sie verzichten auf die Monotonie-Eigenschaft, das heißt ein gültiges Argument kann durch das Hinzufügen weiterer Prämissen ungültig werden.

Dies ist freilich nur möglich, wenn eine andere Konsequenzoperation als in einer klassischen Logik verwendet wird. Ein gängiger Ansatz besteht darin, so genannte Defaults zu verwenden. Ein Default-Schluss ist dann gültig, wenn sich nicht aus einem klassisch-logischen Schluss ein Widerspruch zu ihm ergibt.

Die Schlussfolgerung aus dem gegebenen Beispiel würde dann so aussehen: „Tux ist ein Vogel.“ bleibt die Voraussetzung (prerequisite). Wir kombinieren diese nun mit einer so genannten Rechtfertigung (justification): „Vögel können normalerweise fliegen.“ Aus dieser Begründung schließen wir, dass Tux fliegen kann, solange nichts dagegen spricht. Die Konsequenz lautet also „Tux kann fliegen.“ Erhalten wir nun die Informationen „Tux ist ein Pinguin.“ und „Pinguine können nicht fliegen.“, so ergibt sich ein Widerspruch. Über den Default-Schluss sind wir zu der Konsequenz gelangt, dass Tux fliegen kann. Mit einer klassisch-logischen Schlussweise aber konnten wir nachweisen, dass Tux nicht fliegen kann. In diesem Fall wird der Default revidiert und die Konsequenz des klassisch-logischen Schlusses weiterverwendet. Dieses – hier grob beschriebene − Verfahren wird auch als Reitersche Default-Logik bezeichnet.

• Eintrag in der Stanford Encyclopedia of Philosophy (englisch, inklusive Literaturangaben)Vorlage:SEP/Wartung/Parameter 1 und weder Parameter 2 noch Parameter 3

Wichtige Autoren

• Aristoteles (384-322 v.u.Z.):

In der Analytica Priora Entwicklung der bis ins 19. Jahrhundert verwendeten Syllogistik, einer Vorform der Prädikatenlogik.

• Cicero (106-43 v.u.Z.):

Er übernahm von Aristoteles die Lehre von der Logik und übertrug sie als Ars logica ins Lateinische: De finibus bonorum et malorum.

Seine Topica berufen sich zwar auf Aristoteles. Tatsächlich beruhen sie aber auf der stoischen Logik, die wir ansonsten nur durch Diogenes Laertios kennen.

• Gottfried Wilhelm Leibniz (1646-1716):

Erste Ansätze zu einer symbolischen Logik

• George Boole (1815-1864):

Entwicklung der Booleschen Algebra.

• Charles Sanders Peirce (1839-1914):

Erste Ansätze zur Quantorenlogik, Einführung der Relationslogik, Formulierung einer Theorie der Abduktion.

• Georg Cantor (1845-1918):

Entwicklung der Mengenlehre.

• Gottlob Frege (1848-1925):

Entwicklung der modernen Aussagen- und Prädikatenlogik. Kritik des Psychologismus.

• Edmund Husserl (1859-1938):

Kritik des Psychologismus in der Logik

• Bertrand Russell (1872-1970):

Entdeckte die Russellsche Antinomie.

• Jan Łukasiewicz (1878-1956):

Entwickelte die Polnische Notation, beschäftigte sich mit mehrwertiger Logik

• Alfred Tarski (1901-1983):

Herausragend sind seine Arbeiten zur Modelltheorie und zur formalen Semantik

• Kurt Gödel (1906-1978):

Vollständigkeit der Prädikatenlogik. Unvollständigkeit der Peano-Arithmetik.

Siehe auch: Kategorie:Logiker

Siehe auch

• Abstraktion
• Theorie formaler Sprachen
• Semantik
• Kategorie:Logik
• 

   Portal: Logik – Übersicht zu Wikipedia-Inhalten zum Thema Logik

Klassische Werke

• Aristoteles: Lehre vom Schlusz oder erste Analytik. 3. Auflage. Meiner, Hamburg 1922, ISBN 3-7873-1092-4
• Gottlob Frege: Begriffsschrift, eine der arithmetischen nachgebildete Formelsprache des reinen Denkens. Halle/Saale 1879. Auszugsweise abgedruckt z.B. in: Karel Berka, Lothar Kreiser, Siegfried Gottwald, Werner Stelzner: Logik-Texte. Kommentierte Auswahl zur Geschichte der modernen Logik. 4. Auflage. Akademie-Verlag, Berlin 1986.
• Gottlob Frege: Logische Untersuchungen. Herausgegeben und eingeleitet von Günther Patzig 3. Auflage. Vandenhoeck & Ruprecht, Göttingen 1986, ISBN 3-525-33518-0
• Giuseppe Peano: Notations de logique mathématique. Turin 1894.
• Charles Sanders Peirce: On the algebra of Logic. A contribution to the philosophy of notation. The American Journal of Mathematics 7, 1885
• Jan Łukasiewicz: Logika dwuwartościowa, Przegląd Filosoficzny, 23, 1921, S. 189ff.
• Jan Łukasiewicz, L. Borkowski (Hrsg.): Selected Works. PWN, Warschau 1970.
• Alfred North Whitehead; Bertrand Russell: Principia Mathematica. Cambridge 1910–1913, 2. Aufl. 1925–1927.
• Alfred Tarski: Einführung in die mathematische Logik. 5. Auflage. Vandenhoeck & Ruprecht, Göttingen 1977, ISBN 3-525-40540-5

Literatur

Philosophiebibliographie: Logik – Zusätzliche Literaturhinweise zum Thema

• Karel Berka, Lothar Kreiser: Logik-Texte. Kommentierte Auswahl zur Geschichte der modernen Logik. 4. Auflage. Akademie-Verlag, Berlin 1986.

Geschichte der Logik

• Earline J. Ashworth: The Tradition of Medieval Logic and Speculative Grammar from Anselm to the End of the 17th Century: A Bibliography from 1836 Onwards, Toronto: Pontifical Institute of Medieval Studies 1978
• Innocentius M. Bochenski: Formale Logik, Freiburg-München : Orbis Academicus 2. A. 1956
• Philotheus Boehner: Medieval Logic. An Outline of its Development from 1250 - c. 1400, Manchester: University of Manchester Press 1952
• Alexander Broadie: Introduction to Medieval Logic, Oxford: Clarendon 2. A. 1993
• Heinz W. Enders: Sprachlogische Traktate des Mittelalters und der Semantikbegriff : ein historisch-systematischer Beitrag zur Frage der semantischen Grundlegung formaler Systeme, München : Schöningh 1975 (Veröffentlichungen des Grabmann-Institutes zur Erforschung der Mittelalterlichen Theologie und Philosophie ; N.F., 20) (Münchener Universitäts-Schriften : Fachbereich Katholische Theologie), ISBN 3-506-79420-5
• Desmond Paul Henry: Medieval Logic and Metaphysics: A Modern Introduction, London: Hutchinson 1972
• Ernst Kapp: Der Ursprung der Logik bei den Griechen. Vandenhoeck & Ruprecht, Göttingen 1965, 1994. ISBN 3-525-33228-9
• Gyula Klima: Ars Artium: Essays in Philosophical Semantics, Medieval and Modern, Budapest: Institute of Philosophy of the Hungarian Academy of Sciences 1988
• William Kneale, Martha Kneale: The Development of Logic. Clarendon Press, 1962, 2. A. 1964, ISBN 0-19-824773-7.
• Norman Kretzmann, Eleonore Stump, The Cambridge Translations of Medieval Philosophical Texts, Bd. 1: Logic and the Philosop of Language, Cambridge: CUP 1988
• Norman Kretzmann (Hg.): Meaning and Inference in Medieval Philosophy, Dordrecht: Kluwer 1989
• Benson Mates: Stoic Logic. University of California, Berkeley 1953, ISBN 0-608-11119-8 (englisch) (Books on Demand)
• Lorenzo Minio-Paluello: Twelfth Century Logic. Texts and Studies, Rom: Edizioni di Storia e Letteratura 1956-58
• Ernest A. Moody: Truth and Consequence in Mediaeval Logic, Studies in Logic and the Foundations of Mathematics, Amsterdam, North Holland 1953
• Jan Pinborg: Die Entwicklung der Sprachtheorie im Mittelalter. Münster 1985.
• Jan Pinborg: Logik und Semantik im Mittelalter. Ein Überblick (Problemata 10), Stuttgart-Bad Cannstatt 1972
• Carl Prantl: Geschichte der Logik im Abendlande, 4 Bde., 1855 / Nachdruck Berlin: Akademie-Verlage 1955
• Lambertus Marie de Rijk: Logica modernorum, a contribution to the history of early terminist logic, Wijsgerige teksten en studies 6. 2 Bde., Assen, Van Gorcum 1962-67
• Wilhelm Risse: Die Logik der Neuzeit 2 Bde., Frommann, Stuttgart-Bad Cannstatt 1964, 1970.

Logische Propädeutik

• Ernst Tugendhat, Ursula Wolf: Logisch-semantische Propädeutik. Nachdruck. Reclam, Stuttgart 2001, ISBN 3-15-008206-4 (RUB 8206)
• Wilhelm Kamlah, Paul Lorenzen: Logische Propädeutik. Vorschule des vernünftigen Redens. 3. Auflage. Metzler, Stuttgart u. a. 1996, ISBN 3-476-01371-5
• Axel Bühler: Einführung in die Logik. Argumentation und Folgerung. 3. Auflage. Alber, Freiburg/München 2000, ISBN 978-3-495-47905-6

Formale Logik in der Philosophie

• Jon Barwise, John Etchemendy: The Language of First-Order Logic. CSLI Center for the Study of Language and Information, Leland Stanford Junior University 1991, ISBN 0-937073-74-1
• Ansgar Beckermann: Einführung in die Logik. 2. Auflage. De Gruyter, Berlin u. a. 2003, ISBN 3-11-017965-2
• Wolfgang Detel: Grundkurs Philosophie. Band 1: Logik. Reclam, Stuttgart, 2007, ISBN 978-3-15-018468-4.
• Paul Hoyningen-Huene: Formale Logik. Eine philosophische Einführung. Reclam, Stuttgart 1998, ISBN 3-15-009692-8
• Rüdiger Inhetveen: Logik. Eine dialog-orientierte Einführung. Ed. am Gutenbergplatz, Leipzig 2003, ISBN 3-937219-02-1
• Franz von Kutschera, Alfred Breitkopf: Einführung in die moderne Logik. 8. Auflage. Alber, Freiburg 2007, ISBN 3-495-47977-5
• E. J. Lemmon: Beginning Logic. 2. Auflage. Chapman and Hall, London 1987, ISBN 0-412-38090-0
• Arnold Oberschelp: Logik für Philosophen. 2., verb. Auflage. Metzler, Stuttgart 1997, ISBN 3-476-01545-9
• Paul Ruppen: Einstieg in die formale Logik. Ein Lern- und Übungsbuch für Nichtmathematiker Peter Lang 1996, ISBN 3-906-75685-8
• Benson Mates: Elementare Logik. Prädikatenlogik der ersten Stufe mit Identität. 2. Auflage. Vandenhoeck & Ruprecht, Göttingen 1978, ISBN 3-525-40541-3
• Wesley C. Salmon: Logik. Reclam: Stuttgart 1983, ISBN 3-15-007996-9
• Thomas Zoglauer: Einführung in die formale Logik für Philosophen. 3. Auflage. Vandenhoeck & Ruprecht, Göttingen 2005, ISBN 3-8252-1999-2, ISBN 3-525-03293-5 (UTB für Wissenschaft Bd. 1999)

Formale Logik in der Mathematik

• Heinz-Dieter Ebbinghaus, Jörg Flum, Wolfgang Thomas: Einführung in die mathematische Logik. 4. Auflage. Spektrum, Akademie, Heidelberg u. a. 1998, ISBN 3-8274-0130-5 (Spektrum-Hochschultaschenbuch)
• Wolfgang Rautenberg: Einführung in die Mathematische Logik. Ein Lehrbuch. 2. Auflage. Vieweg, Braunschweig u. a. 2002, ISBN 3-528-16754-8
• Donald W Barnes, John M. Mack: An Algebraic Introduction to Mathematical Logic. Springer, Berlin 1975, ISBN 3-540-90109-4. (Ein sehr mathematischer Zugang zur Logik.)

Formale Logik in der Informatik

• Uwe Schöning: Logik für Informatiker. 5. Auflage. Spektrum, Akademie, Heidelberg u. a. 2000, ISBN 3-8274-1005-3 (Spektrum-Hochschultaschenbuch)
• Bernhard Heinemann, Klaus Weihrauch: Logik für Informatiker. Eine Einführung. 2. Auflage. Teubner, Stuttgart 1992, ISBN 3-519-12248-0 (Leitfäden und Monographien der Informatik)

Hilfsmittel

• Nikolaj I. Kondakov: Wörterbuch der Logik. 2. Auflage. Bibliographisches Institut, Leipzig 1983.
• Jürgen Mittelstraß (Hrsg.): Enzyklopädie Philosophie und Wissenschaftstheorie. 4 Bände, Bibliographisches Institut, Mannheim u.a. 1980-1996, ISBN 3-411-01603-5

Einzelnachweise

1. ↑ Kuno Lorenz: Logik, II.. Die antike Logik in Historisches Wörterbuch der Philosophie, Bd. 5, 362 nach E. Kapp: Der Ursprung der Logik bei den Griechen, 1965, 25 und mit Verweis auf Cicero: De finibus 1, 7, 22

Weblinks

Geschichte

• Susanne Bobzien: „Ancient Logic“ in der Stanford Encyclopedia of Philosophy (englisch, inklusive Literaturangaben)
• Volker Peckhaus: Logik im 19. Jahrhundert
• Richard Zach: Geschichte der Logik von 1900 bis 1935
• Klaus Glashoff: Modern Interpretation of Ancient Logic
• Catarina Dutilh Novaes: 14th Century Logic after Ockham
• Raul Corazzon: An Annotated Bibliography on the History of Logic
• Thomas Case: Logic, in: Encyclopedia Britannica 1911
• Johan van Benthem: Logic in Philosophy, in: Dale Jacquette (Hg.): Handbook of the Philosophy of Logic

Allgemein

• Graeme Forbes: Logic, philosophy of, in E. Craig (Hg.): Routledge Encyclopedia of Philosophy, London 1998.
• Ausführliche Einführung in die Logik. Prädikatenlogik der ersten Stufe mit Identität
• Lexikon der Philosophie: Logik
• Logiksoftware für Unterrichtszwecke
• Logiksoftware (etwas ältere umfängliche Linksammlung)
• Introduction to Computational Logic (Skripte, englisch)
• Achim Wagenknecht: Eine ganz kurze Einführung in die Logik
• Online-Logik-Kurse
• Crashkurs Aussagen- und Prädikatenlogik
• Externe Links zu Autoren / Forscher / Klassiker
• L. Geldsetzer: Logik Bibliographie mit Auswahlliteratur zu Einzelthemen
• Immanuel Kant: Logik – eine heute veraltete Darstellung auf dem Stand des Jahres 1800
• Universität Bern -Logik mit Übungen - Script für eine Logikvorlesung an der Uni Bern in 12 Lektionen mit Online-Test zu jeder Lektion
• Peter H. Starke: Logische Grundlagen der Informatik Umfangreiches Skript, das auch als PDF downloadbar ist, HU Berlin
• Logic, in: Polimetrica Onlus (Hg.): “The Language of Science”, ISSN 1971-1352