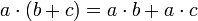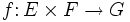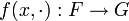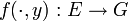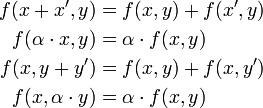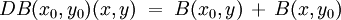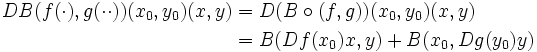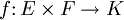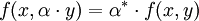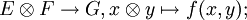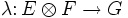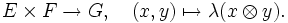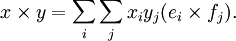Bilinear

Im mathematischen Teilgebiet der linearen Algebra und verwandten Gebieten verallgemeinern die bilinearen Abbildungen die verschiedensten Begriffe von Produkten (im Sinne einer Multiplikation). Die Bilinearität entspricht dem Distributivgesetz

$a \cdot (b + c) = a \cdot b + a \cdot c$

bei der normalen Multiplikation.

Definition

Eine bilineare Abbildung ist eine 2-multilineare Abbildung, das heißt eine Abbildung

$f\colon E\times F\to G$

so dass für jedes (fest gewählte) x aus E und y aus F die partiellen Abbildungen

$f(x, \cdot): F \to G$

und

$f(\cdot, y): E \to G$

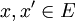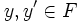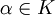lineare Abbildungen sind. Für beliebige $x, x' \in E$, $y, y' \in F$ und $\alpha \in K$ gilt demnach

$\begin{align} f(x + x', y) &= f(x, y) + f(x', y)\\ f(\alpha \cdot x, y) &= \alpha \cdot f(x, y)\\ f(x, y + y') &= f(x, y) + f(x, y')\\ f(x, \alpha \cdot y) &= \alpha \cdot f(x, y) \end{align}$

Dies impliziert, dass E, F und G drei K-Moduln oder K-Vektorräume über dem (demselben) Körper K sind.

Vergleicht man eine bilineare Funktion f mit dem Distributivgesetz, dann tritt f an die Stelle der Multiplikation: f(x,y) ersetzt das Produkt $x \cdot y$.

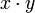Stetigkeit und Differenzierbarkeit

Bilineare Abbildungen mit endlich-dimensionalem Definitionsbereich sind immer stetig.

Ist eine bilineare Abbildung B stetig, ist sie auch total differenzierbar und es gilt

$DB(x_0,y_0)(x,y) \;=\; B(x_0,y)\,+\,B(x,y_0)$

Unter Anwendung der Kettenregel folgt daraus, dass zwei differenzierbare Funktionen, die mit einer bilinearen Abbildung verknüpft sind, mit der Verallgemeinerung der Produktregel abgeleitet werden können: Seien f,g total differenzierbare Funktionen, dann gilt

$\begin{align}DB(f(\cdot),g(\cdot \cdot))(x_0,y_0)(x,y) &= D(B \circ (f,g))(x_0,y_0)(x,y)\\ &= B(Df(x_0)x,y) + B(x_0,Dg(y_0)y)\end{align}$

Beispiele

Sämtliche gemeinhin übliche Produkte sind bilineare Abbildungen: die Multiplikation in einem Körper (reelle, komplexe, rationale Zahlen) oder einem Ring (ganze Zahlen, Matrizen), aber auch das Vektor- oder Kreuzprodukt, und Skalarprodukt.

Ein Spezialfall der bilinearen Abbildungen sind die Bilinearformen. Bei diesen ist der Wertebereich G mit dem Skalarkörper K der Vektorräume E und F identisch.

$f \colon E \times F \to K$

Bilinearformen sind für die analytische Geometrie und Dualitätstheorie wichtig.

In der Bildverarbeitung wird eine bilineare Filterung zur Interpolation eingesetzt.

Weitere Eigenschaften

Symmetrie, Antisymmetrie (für F = E) und andere Eigenschaften sind wie im allgemeineren Fall der multilinearen Abbildungen definiert.

Eine bilineare Abbildung 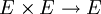$E\times E\to E$ macht E zu einer Algebra.

Im Falle komplexer Vektorräume betrachtet man auch sesquilineare („anderthalb“-lineare) Abbildungen, welche im zweiten (oder ggf. im ersten) Argument antilinear sind, das heißt dass

$f(x, \alpha \cdot y) = \alpha^* \cdot f(x, y)$

(wobei * die komplexe Konjugation bezeichnet), während alle anderen obigen Gleichungen bestehen bleiben.

Bezug zu Tensorprodukten

Bilineare Abbildungen werden im folgenden Sinne durch das Tensorprodukt klassifiziert: Ist

$f\colon E\times F\to G$

eine bilineare Abbildung, so gibt es eine eindeutig bestimmte lineare Abbildung

$E\otimes F\to G,x\otimes y\mapsto f(x,y);$

umgekehrt definiert jede lineare Abbildung

$\lambda\colon E\otimes F\to G$

eine bilineare Abbildung

$E\times F\to G,\quad (x,y)\mapsto\lambda(x\otimes y).$

Diese beiden Konstruktionen definieren eine Bijektion zwischen dem Raum der bilinearen Abbildungen 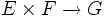$E\times F\to G$ und dem Raum der linearen Abbildungen $E\otimes F\to G$.

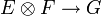Bilineare Abbildungen über endlich dimensionalen Vektorräumen

Sind E und F endlich dimensionale K-Vektorräume mit beliebig gewählten Basen 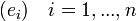$(e_i) \quad i=1,...,n \quad$ von E und 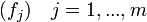$(f_j) \quad j=1,...,m \quad$ von F, dann gibt es für ein beliebiges x aus E die Darstellung

x =	∑	xiei
	i

mit Koeffizienten x_i aus K und analog für ein beliebiges y aus F die Darstellung

y =	∑	yjfj.
	j

Mit den Rechenregeln der bilinearen Abbildung ergibt sich dann

$x\times y = \sum_i \sum_j x_i y_j (e_i \times f_j).$

Die bilineare Abbildung ist also durch die Bilder aller geordneten Paare der Basisvektoren von E und F bestimmt. Ist G ebenfalls ein K-Vektorraum, so spannt das Bild 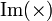$\operatorname{Im}(\times)$ einen maximal n * m dimensionalen Untervektorraum von G auf. Im allgemeinen ist das Bild einer bilinearen Abbildung zwischen Vektorräumen aber kein Untervektorraum.

Für Bilinearformen sind die 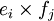$e_i \times f_j$ aus K, so dass sie in naheliegender Weise in einer Matrix notiert werden koennen. Diese Matrix ist dann die Koordinatendarstellung der Bilinearform bezüglich der gewählten Basen.