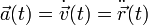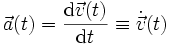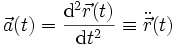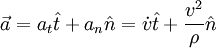Bremsung

Physikalische Größe
Name	Beschleunigung
Größenart	Beschleunigung
Formelzeichen der Größe	a
Größen- und Einheiten- system Einheit Dimension SI m·s-2 L·T-2 CGS cm·s-2 L·T-2 Planck Planck-Beschleunigung ħ-1/2·G-1/2·c7/2

Beschleunigung ist die Änderung der Geschwindigkeit eines Körpers. Das Wort wird, sogar innerhalb der physikalischen Fachsprache, in zwei etwas verschiedenen Bedeutungen benutzt:

• Im alltäglichen Wortsinn, aber auch z. B. in dem Begriff Teilchenbeschleuniger, ist eine Erhöhung des Betrages der Geschwindigkeit gemeint;
• im allgemeineren Sinn bezeichnet Beschleunigung jede Änderung des Geschwindigkeitsvektors, also auch eine Abnahme des Betrages (Verzögerung oder Abbremsung) oder eine Richtungsänderung bei gleich bleibendem Geschwindigkeitsbetrag. Die Beschleunigung in diesem Sinne ist die zeitliche Ableitung des Geschwindigkeitsvektors oder die zweite zeitliche Ableitung des Ortsvektors.

$\vec a(t) = \dot{\vec v}(t) = \ddot{\vec r}(t)$

Die SI-Einheit der Beschleunigung ist m/s².

Die Beschleunigung ist wie die Geschwindigkeit eine gerichtete Größe (Vektor). Sie ist eine der wesentlichen Größen der klassischen Mechanik, deren Dynamik (Änderung der Beschleunigung unter Einwirkung von Kräften) erstmals von Isaac Newton beschrieben wurde (siehe auch Newton-Axiome).

Um einen Körper zu beschleunigen, ist immer eine Kraft notwendig.

Für Systeme mit konstanter Masse in einem Inertialsystem ergibt sich die Beschleunigung aus dem Verhältnis von Kraft zu Masse

$\vec a=\frac{\vec F}{m}$.

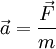Beschleunigungsvorgänge spielen in allen bewegten Systemen, wie z. B. Fahrzeugen, Flugzeugen oder Aufzügen, eine wichtige Rolle und sind aufgrund der in diesem Zusammenhang auftretenden Trägheitskräfte für die darin beförderten Menschen und Sachen meist deutlich spürbar.

Physikalische Definition

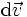Die Beschleunigung $\vec a$ ist eine physikalische Größe aus der Kinematik, die definiert ist als die Geschwindigkeitsänderung $\mathrm{d} \vec{v}$ pro Zeitintervall dt. Sie ist also die zeitliche Ableitung

$\vec a(t) = \frac{\mathrm{d}\vec v(t)}{\mathrm{d}t} \equiv \dot{\vec v}(t)$

Da die Geschwindigkeit die Ableitung des Ortes nach der Zeit ist, kann man die Beschleunigung auch als zweite Ableitung des Ortsvektors 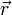$\vec r$ darstellen

$\vec a(t) = \frac{\mathrm{d}^2\vec r(t)}{\mathrm{d} t^2} \equiv \ddot{\vec r}(t)$

Eine mittlere Beschleunigung kann aus der Differenz der Geschwindigkeiten Δv = v(t₂) − v(t₁) zu zwei verschiedenen Zeitpunkten t₁ und t₂ dividiert durch das zwischen den beiden Zeitpunkten verstrichene Zeitintervall Δt = t₂ − t₁ berechnet werden

$\vec a = \frac{\Delta \vec v}{\Delta t}$.

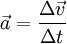Der Geschwindigkeitsvektor 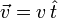$\vec{v}=v\,\hat{t}$ setzt sich zusammen aus dem Geschwindigkeitsbetrag v und dem Tangenteneinheitsvektor 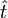${\hat{t}}$. Bildet man nun die Ableitung dieses Ausdrucks erhält man die Beschleunigung. Die zeitliche Ableitung des Tangenteneinheitsvektors kann über die Bogenlänge s berechnet werden:

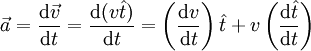$\vec{a}=\frac{\mathrm d\vec v }{\mathrm dt}=\frac{\mathrm d(v\hat t)}{\mathrm dt}=\left( \frac{\mathrm dv}{\mathrm dt} \right)\hat t +v\left( \frac{\mathrm d\hat t}{\mathrm dt} \right)$    mit    $\frac{\mathrm d\hat t}{\mathrm dt}=\underbrace{\frac{\mathrm d\hat t}{\mathrm ds}}_{\hat n/\rho}\underbrace{\frac{\mathrm ds}{\mathrm dt}}_{v}=\frac{v}{\rho} \hat n$

$\vec a =a_{t}\hat{t}+a_{n}\hat n = \dot{v}\hat t +\frac{v^{2}}{\rho } \hat n$

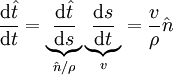
Dabei ist ρ der Krümmungsradius der Bahn und 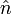$\hat n$ der Normaleneinheitsvektor quer zur Bahnkurve in Richtung des Krümmungsmittelpunkts.

Die Beschleunigung $\vec a$ kann aufgeteilt werden in eine zur Bewegungsrichtung $\vec v$ parallelen Beschleunigung (Tangentialbeschleunigung)

$a_{t}=\dot{v}$

und eine senkrecht dazu stehende Normalbeschleunigung

$a_{n}=\frac{v^{2}}{\rho }$.

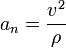Die zeitliche Ableitung der Beschleunigung (also die dritte Ableitung des Ortsvektors nach der Zeit) ist der Ruck:

$\vec {j}(t)= \dot \vec {a}(t)=\ddot \vec {v}(t) = {\mathrm d^3\vec {x}(t)\over \mathrm{d}t^3}$,

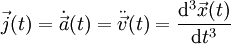Sonderfälle der Beschleunigung

• Beschleunigung $\vec a = \vec 0$:

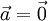Die Geschwindigkeit bleibt in Betrag und Richtung unverändert, der Körper verharrt in Ruhe oder in gleichförmiger Bewegung.

• Konstante Beschleunigung in (bzw. entgegen der) Richtung der Geschwindigkeit (sowohl Richtung als auch Betrag der Beschleunigung sind konstant) führt laut klassischer Mechanik (nach Newton) zu geradliniger Bewegung mit zeitlich gleichförmig wachsender (bzw. abnehmender) Geschwindigkeit (Gleichmäßig beschleunigte Bewegung).

Nach der speziellen Relativitätstheorie gilt diese Linearität aber nur näherungsweise bei nichtrelativistischen Geschwindigkeiten: 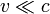$v \ll c$ (c: Lichtgeschwindigkeit).

• Eine Kreisbewegung mit konstantem Geschwindigkeitsbetrag kommt zustande, wenn eine konstante Zentripetalbeschleunigung besteht. Diese Beschleunigung ist nach innen auf den Kreismittelpunkt hin gerichtet. Ein mitbewegter Beobachter hingegen spürt eine gleich große Beschleunigung vom Mittelpunkt weg nach außen (Zentrifugalbeschleunigung).
• Beim freien Fall auf der Erde werden alle Körper mit der Fallbeschleunigung g = 9,80665 m/s² (DIN 1305) in Richtung Erdmittelpunkt beschleunigt. Allerdings gibt es regionale Schwankungen, da die Erdgestalt von einer Kugel abweicht (Erdabplattung) und der innere Aufbau der Erde nicht völlig homogen ist (Schwereanomalie). In der Regel wird bei allgemein gültigen Berechnungen der Näherungswert 9,81 m/s² benutzt.
• Bei einem Stoß zwischen zwei Festkörpern können während des kurzen Zeitraums der Berührung extrem hohe Beschleunigungen auftreten.

Ruck

Der Ruck, die zeitliche Änderung einer Beschleunigung, hat z. B. eine Bedeutung bei der dynamischen Anregung von Maschinen und anderen schwingungsfähigen Systemen. So vollführt bei einer Autofahrt der Beifahrer einen „Kopfnicker“, wenn der Fahrer zu schnell einkuppelt. Die zeitliche Änderung einer Zentripetalbeschleunigung heißt Querruck.

Messung der Beschleunigung

Es existiert eine Vielzahl von Beschleunigungssensoren für verschiedene Anwendungen, von hohen Messbereichen (z. B. +/- 50.000 g) bis zu hochgenauen Messungen. Dies ermöglicht durch zweifache Integration über die Zeit eine Ortsbestimmung von Flugzeugen über einen mittellangen Zeitraum (z. B. für den Fall, dass das GPS-System ausfällt.)

Beispiele für die Größe von Beschleunigungen

• Beim freien Fall im Schwerefeld der Erde beträgt die Beschleunigung g = 9,81 m/s². Damit wird (ohne Luftwiderstand) eine Geschwindigkeit von 100 km/h in 2,83 Sekunden erreicht.
• Bei Nähmaschinen wirken auf die Nadel Beschleunigungen von bis zu 6.000 g.
• Bei einer Waschmaschine wirken im Schleudergang mehr als 300 g auf den Trommelinhalt.
• Beim Fahrradfahren treten Beschleunigungen von etwa 1 m/s² auf (Freizeitfahrer) und bei Sportprofis etwa 2 m/s².
• Ein Mittelklassewagen kann Beschleunigungen bis zu 3 m/s² und Autos höherer Klasse sogar mehr als 4 m/s² hervorbringen.
• Beim Bremsen eines Autos treten negative Beschleunigungen von bis zu 10,5 m/s² auf.
• Bei den Dragster-Fahrzeugen der Top-Fuel-Klasse treten beim Start +6 g (60 m/s²) und beim Abbremsen −6 g an Beschleunigung auf.
• Ein vollbeladener Jumbo-Jet erfährt eine Beschleunigung von etwa 1,6 m/s².
• Der ICE erreicht eine Beschleunigung von etwa 0,5 m/s², ein moderner S-Bahn-Triebwagen sogar 1,0 m/s².
• Während der ersten Schritte eines Sprints wirken Beschleunigungen von etwa 4 m/s² auf den Sportler.
• Die Kugel beim Kugelstoßen wird bei der Abstoßphase mit etwa 10 m/s² beschleunigt.
• Ein Tennisball kann Beschleunigungen bis zu 10.000 m/s² erfahren.
• Tischzentrifugen im Laborbedarf können Beschleunigungen von 12.000 g erzielen.
• Ultrazentrifugen im Laborbedarf können Beschleunigungen von 200.000 g erzielen.
• Auf der Achterbahn Silverstar im Europa-Park herrschen Vertikalbeschleunigungen von bis zu 4 g (40 m/s²).
• Bei Nesselzellen wird der Stachel mit bis zu 5.410.000 g beschleunigt.
• Bei einer Atombombenexplosion werden Beschleunigungen von bis zu 100 Milliarden g erreicht.
• Am Ereignishorizont eines Schwarzen Lochs mit etwa 3 Sonnenmassen werden etwa 500 Milliarden g erzeugt.

Umgangssprachliche Verwendung

• Bei Kraftfahrzeugen wird die erreichbare Beschleunigung als ein wesentlicher Parameter zur Klassifizierung der Leistung verwendet. Es wird dabei jedoch nicht direkt die physikalische Größe angegeben (die ohnehin je nach Geschwindigkeit und Fahrzustand verschieden ist), sondern meist eine Art Mittelwert in der Form „Sekunden von 0 auf 100 km/h“ (auch 160 oder 200 km/h).
• Die „Kosmologische Beschleunigung“ ist ein für die Expansion des Universums verwendeter Ausdruck.
• In der Psychologie wird die subjektiv empfundene zunehmende Geschwindigkeit im täglichen Leben mit der Alterung in Verbindung gebracht (siehe hierzu auch Entschleunigung, Gerontologie).

siehe auch

• Dynamik (Physik)

Weblinks

• Programm, mit dem Bewegungen mit beliebigen (auch nicht konstanten!) Beschleunigungen berechnet werden können
• Untersuchungen zur Beschleunigung an der Atwoodschen Fallmaschine