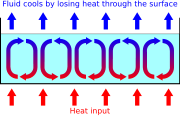
- Bénardsche Zelle
-
Schematische Darstellung der Bénard-Zellen in SeitenansichtBeim Bénard-Experiment (Bénard-Effekt, Bénard-System, Bénard-Zellen, Rayleigh-Benard-Experiment) wird eine dünne, homogene Flüssigkeitsschicht die sich in einem festen Behältnis und in einem Gravitationsfeld befindet von der Unterseite erhitzt, während die Oberseite durch Kühlung auf einer niedrigeren Temperatur gehalten wird. Es bilden sich geometrisch strukturierte vertikal angeordnete Konvektionszellen aus (siehe Bild rechts). Besonders in deren Randbereich findet der Flüssigkeitsaustausch zwischen der heißen Flüssigkeit von unten und der abgekühlten Flüssigkeit von oben statt. Die Zellenstrukturen sind in der Draufsicht typisch linear oder hexagonal. Im zweiten Fall bildet sich in der Mitte der Sturktur ein Strömungszentrum aus. Der Zustand wird zwischen einem Zustand fester Schichtung (geringe oder keine Temperaturdifferenz) und einem Zustand mit reinem Chaos (sehr große Temperaturdiffernz) eingeordnet. Mit zunehmender Temperaturdifferenz nimmt die Komplexität der Strukturen in einem solchen System gemäß Lorenz zu.
Das Experiment wurde nach Henri Bénard benannt, der es 1900 in seiner Dissertation erstmals ausführlich beschrieb. Teilweise wird das Bénard-Experiment in der Literatur auch als Rayleigh-Benard-Experiment beschrieben und bezieht diese Erweiterung auf Baron Rayleigh.
Der Bénard-Marangoni-Effekt (nach Carlo Marangoni) wird vielfach mit dem hier beschriebenen verwechselt. Bei diesem verwandten Effekt wird das Konvektionsmedium jedoch von anderen, nicht-festen Medien begrenzt. [1]
Inhaltsverzeichnis
Beschreibung des Experiments
Ausbildung von Bénard-Zellen in einer Luftschicht
Bénard-ZellenEine Flüssigkeit dehnt sich an der warmen Unterseite aus und kann aufgrund der geringeren Dichte nach oben steigen, während die kältere, dichtere Flüssigkeit im oberen Bereich nach unten sinken kann. Die Viskosität der Flüssigkeit wirkt diesem entgegen.
Ist die Temperaturdifferenz ΔT zwischen Boden und Oberfläche gering, überwiegt die Viskosität und die Wärme wird ohne gleichzeitigen Stofftransport durch homogene Wärmeleitung von unten nach oben befördert. Oberhalb eines kritischen Temperaturunterschiedes ΔTkrit,1 wird dieser Zustand instabil, der Wärmetransport findet durch Wärmekonvektion statt. Die Flüssigkeit kommt aufgrund der Dichteunterschiede zwischen Ober- und Unterseite in Bewegung. Es treten regelmäßig geformte Konvektionszellen meist in Sechseck- oder Rollenmuster auf, die Bénard-Zellen. Steigt die Temperaturdifferenz zwischen Ober- und Unterseite der Flüssigkeit weiter an, setzen ab einem zweiten kritischen Wert ΔTkrit,2 Periodenverdopplungen ein. Das System gelangt auf der Feigenbaum-Route ins Chaos, es entwickelt sich Turbulenz, wie zuerst Albert J. Libchaber Ende der 1970er Jahre zeigte.
Zur Durchführung des Experiments eignen sich besonders Flüssigkeiten mit einer geringen Viskosität, z. B. dünnes Öl oder Gele. Es wurde aber auch schon mit flüssigem, tiefgekühltem Helium durchgeführt. Der Wärmeausdehnungskoeffizient der Flüssigkeit muss positiv sein. Das Temperatur- und Strömungsgeschwindigkeitsfeld dieses Experiments muss der Navier-Stokes-Gleichung, der Wärmeleitungsgleichung und der Kontinuitätsgleichung (Erhaltungssatz der Masse) genügen.
Bedeutung
Granulation auf der Sonnenoberfläche. Bilddurchmesser ca. 35.000 kmDas Bénard-Experiment ist ein Standardbeispiel für die Ausbildung von dissipativen Strukturen in konvektiven, offenen Systemen fern vom thermodynamischen Gleichgewicht. Ähnliches Verhalten kann im Prinzip in allen viskosen Medien auftreten. Neben Modellexperimenten mit dünnen Ölschichten kann man ähnliches Verhalten auch im Erdmantel, dem Ozean oder in der Atmosphäre (z. B. in Form von sechseckigen oder rollenförmigen Wolkenstrukturen) entdecken.
Die Untersuchung der atmosphärischen Konvektion war der Ausgangspunkt, der zur Entdeckung des deterministischen Chaos durch den Meteorologen Edward Lorenz Anfang der 1960er Jahre führte. Er untersuchte den Übergang der Wärmekonvektion in einen turbulenten Zustand innerhalb eines Mediums. Das von Lorenz zu diesem Zweck aufgestellte System (Lorenz-Attraktor) aus drei autonomen Differentialgleichungen zeigte erstmals am Computer nachvollziehbar chaotische Schwingungen innerhalb eines deterministischen Systems.
Beispiele:
- Granulation auf der Sonnenoberfläche, siehe Granulation (Astronomie).
- Thermische Vertikalbewegung im Erdmantel, siehe Mantelkonvektion.
- Entmischung von Pigmenten mit unterschiedlichen Dichten in bestimmten Lacken während der Trocknung.
Siehe auch
Literatur
- Edward Lorenz: Deterministic nonperiodic flow. In: Journal of the Atmospheric Sciences. 20/1963, S. 130-141
- Gottfried Jetschke: Mathematik der Selbstorganisation. Verlag Harri Deutsch, Frankfurt a. M. 1989, ISBN 3-81711282-3
Weblinks
- Turbulente rotierende Konvektion (Technische Universität Eindhoven, Niederlande; englisch) mit Darstellung einer präzisierten Rayleigh-Bénard-Zelle nach L. Kadanoff
Wikimedia Foundation.
