Torische Linse

Abb. 1: Torische Linsenoberfläche als „Käppchen” (rechtsoben) von einem Torus (hier mit R = 1,2 r).

Eine torische Linse^[1] ist eine Linse, die in zwei senkrecht zueinander stehenden Richtungen zwei unterschiedliche Brechwerte hat. Eine der Linsenoberflächen hat dabei die Form eines „Käppchens” von einem Torus (s. Abb. 1), die andere ist meistens sphärisch. Torische Linsen werden insbesondere verwendet in Brillengläsern, Kontaktlinsen und Intraokularlinsen, zur Korrektur des Astigmatismus.

Torus

Abb. 2: Ein Torus entsteht, wenn ein Kreis r um eine in derselben Ebene liegende Achse (hier die z-Achse) rotiert, die sich im Abstand R der Kreismitte befindet.

Abb. 3: V.l.n.r.: Spindeltorus, Horntorus und Ringtorus. Wenn der große Radius R kleiner wird (hier von rechts nach links), „schliesst“ sich der Torus; bei R = 0 entartet er in eine Kugel.

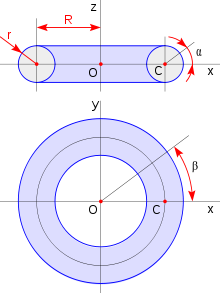
Ein Torus entsteht, wenn ein Kreis mit Radius r um eine Achse rotiert (z-Achse in Abb. 2), die in derselben Ebene liegt wie der Kreis. Der Mittelpunkt dieses Kreises folgt dabei einer kreisförmigen Bahn mit Radius R um die Rotationsachse. Wenn R > r, erhält man einen Ringtorus. Wenn R = r, ist die Öffnung in den Mittelpunkt des Rotationskreises zusammengeschrumpft; man spricht hier von einem Horntorus. Wenn R < r, spricht man von einem Spindeltorus; hier bleiben von der Öffnung nur zwei Vertiefungen übrig, deren Tiefe verschwindet, wenn R → 0 geht. Wenn R = 0, ist der Torus in eine Sphäre mit Radius r entartet. (Siehe Abb. 3.)

Beschreibung

Der größte Krümmungsradius der torischen Linsenoberfläche ist R + r (siehe Abb. 2); der entsprechende kleinste Brechwert ist S = (n – 1) / (R + r), wenn n die Brechungszahl des Glases ist. Dem kleinsten Krümmungsradius, r, entspricht der größte Brechwert, s = (n – 1) / r. Da R + r > r ist, ist S < s. Die Differenz, s − S, wird in der Augenheilkunde und Augenoptik die Zylinderkorrektur^[2] genannt. Das Glas verhält sich etwa wie eine Kombination einer sphärischen Linse mit Brechwert s und einer Zylinderlinse met Brechwert s – S.

Bemerke, dass die maximale und die minimale Krümmung beide kreisförmig sind. Im Gegensatz zu dem was viele meinen, ist die torische Linsenoberfläche also kein Teil eines Rotationsellipsoids.

Wirkung

Lichtstrahlen, die in der (x,y)-Ebene des Torus (siehe Abb. 2) einfallen, werden entsprechend dem größten Krümmungsradius, R + r, also dem kleinsten Brechwert S = (n – 1) / (R + r), gebrochen.

Lichtstrahlen in einer Ebene durch die z-Achse des Torus (siehe Abb. 2) werden entsprechend dem kleinsten Krümmungsradius, r, also dem größten Brechwert s = (n – 1) / r, gebrochen.

Es gibt somit zwei verschiedene Brechwerte in senkrecht zu einander stehenden Richtungen. In den Zwischenrichtungen verläuft der Brechwert fließend vom kleinsten zum größten Wert, oder umgekehrt. Dies kompensiert die astigmatischen Abweichungen des Auges.

Atorische Linse

Computergesteuerte Entwurf-, Schleif- und Polierverfahren ermöglichen es heutzutage, in einem größeren Blickfeld gute Korrekturen zu erreichen, indem man bestimmte Abweichungen von der Torusform einbringt. In diesem Fall spricht man von einer atorischen (wörtlich: „nicht-torischen“) Linse.^[3][4]

Weblinks

• Carl Zeiss Vision
• Astigmatismus Schweiz

Einzelnachweise

1. ↑ Von der Mathematik her würde man eher den Begriff toroidale Linse erwarten. Im Bereich der Augenheilkunde und Augenoptik ist jedoch der Begriff torische Linse üblich. Vermutlich basiert sich das darauf, dass man im Englischen unter torus nur den Rotationskörper eines Kreises versteht und den Begriff toroid nur für Rotationskörper anderer flacher Figuren verwendet.
2. ↑ Diese korrigiert den Astigmatismus des Auges. Der Term Zylinder basiert hier auf eine mathematische Approximation, die nur bei kleinen Korrekturwerten gültig ist.
3. ↑ D. Meister: Principles of Atoric Lens Design. In: Lens Talk. Vol. 27, No. 3, 1998 (PDF).
4. ↑ D. Volk: Aspheric Lenses. (chapter 50 in Duane's Ophthalmology (Lippinkott, Wilkins & Williams / Wolters-Kluwer Health, Chicago, USA).