Stichprobenkovarianz

Die Stichprobenkovarianz oder empirische Kovarianz (oft auch einfach Kovarianz) ist in der Statistik eine nichtstandardisierte Maßzahl für den (linearen) Zusammenhang zweier statistischer Variablen. Die korrigierte Stichprobenkovarianz ist eine erwartungstreue Schätzung der Kovarianz einer Grundgesamtheit mittels einer Stichprobe.

Ist die Kovarianz positiv, dann gehen kleine Werte der einen Variable überwiegend einher mit kleinen Werten der anderen Variable und gleichfalls für große Werte. Für eine negative Kovarianz ist das genau umgekehrt.

Definition

Ist (x_i,y_i) eine Datenreihe (Stichprobe) zweier statistischer Variablen X und Y, dann ist die Stichprobenkovarianz definiert als:

$s_{xy}:=\frac1n \sum_{i=1}^n (x_i -\bar{x})(y_i-\bar{y})$

mit $\bar{x}=\frac 1n \sum_{i=1}^n x_i$ und $\bar{y}=\frac 1n \sum_{i=1}^n y_i$ die arithmetischen Mittel der Daten.

Die Stichprobenkovarianz misst die gemeinsame Streuung der Beobachtungsdaten einer Stichprobe. Dabei wird die mittlere Abweichung der Beobachtungsdaten von den Mittelwerten $(\bar{x},\bar{y})$ berechnet.

Oft wird auch die korrigierte Stichprobenkovarianz genutzt:

$\hat{\sigma}_{xy}:=\frac1{n-1} \sum_{i=1}^n (x_i -\bar{x})(y_i-\bar{y})$

Konstruktion der Kovarianz

Konstruktion der Kovarianz.

Der blaue Datenpunkt rechts oben in der Grafik hat einen positiven Beitrag zur Kovarianz:

$\underbrace{(x_i-\bar{x})}_{>0}\times\underbrace{(y_i-\bar{y})}_{>0}>0$.

Dies gilt für alle Datenpunkte im Quadranten I, mit $x_i>\bar{x}$ und $y_i>\bar{y}$. Diese Betrachtungen kann man analog für die Datenpunkte in den anderen Quadranten fortsetzen:

• Datenpunkte in Quadrant I: positiver Beitrag zur Kovarianz,
• Datenpunkte in Quadrant II: negativer Beitrag zur Kovarianz,
• Datenpunkte in Quadrant III: positiver Beitrag zur Kovarianz und
• Datenpunkte in Quadrant IV: negativer Beitrag zur Kovarianz.

Gibt es einen "positiven" Zusammenhang zwischen den Datenpunkten, dann werden die meisten Datenpunkte (wie im rechten Beispiel) im Quadranten I und III liegen und viele positive Beiträge zur Kovarianz liefern. Die wenigen Datenpunkte in den Quadranten II und IV liefern zwar negative Beiträge, aber die positiven Beiträge werden überwiegen, d.h. die Kovarianz ist positiv. Gibt es einen "negativen" Zusammenhang, dann folgt mit der gleichen Argumentation, dass die Kovarianz negativ ist.

Korrigierte Stichprobenkovarianz

Um aus einer Stichprobe eine Schätzung der unbekannten Kovarianz σ_xy der Grundgesamtheit zu erhalten wird die korrigierte Stichprobenkovarianz genutzt:

$\hat{\sigma}_{xy} = \frac{1}{n-1}\sum_{i=1}^n{(x_i-\bar{x}) (y_i-\bar{y})}$

Bei einer einfachen Zufallsstichprobe haben die Stichprobenvariablen X_i und Y_i die Kovarianz Cov(X_i,Y_i) = σ_xy. Unter Annahme einer bivariaten Normalverteilung der Stichprobenvariablen (X_i,Y_i) und mit Hilfe der Maximum-Likelihood-Methode ergibt sich die Schätzfunktion

$S_{XY} = \frac{1}{n}\sum_{i=1}^n (X_i-\bar{X})(Y_i-\bar{Y})$.

Es stellt sich jedoch heraus, dass der Erwartungswert $E(S_{XY})= \tfrac{n-1}{n}\sigma_{xy}$ ist, d.h. die Schätzfunktion S_XY ist nicht erwartungstreu (also verzerrt).

Die korrigierte Stichprobenkovarianz ist jedoch unverzerrt. Im Rahmen der induktiven Statistik wird daher immer die korrigierte Stichprobenkovarianz verwendet.

Stichprobenkovarianz vs. Korrigierte Stichprobenkovarianz

Im Rahmen der deskriptiven Statistik stellt sich die Frage, ob man besser den Faktor $\tfrac1{n-1}$ oder $\tfrac1n$ verwenden soll. Allgemein hängt es vom Ziel der Analyse (bzw. den Eigenschaften der Stichprobe) ab.

• Ist es das Ziel die Kovarianz einer Grundgesamtheit zu schätzen, dann ist wegen der Eigenschaft der Erwartungstreue $\hat{\sigma}_{xy}$, also der Faktor $\tfrac{1}{n-1}$ zu verwenden. Dafür sollte aber der Rückschluss auf die Grundgesamtheit möglich sein, z. B. die Stichprobe eine einfache Zufallsstichprobe sein.
• Ist es das Ziel die Daten nur deskriptiv zu beschreiben, dann kann man $\hat{\sigma}_{xy}$ oder s_xy verwenden. Dies ist z. B. der Fall, wenn der Rückschluss auf die Grundgesamtheit nicht gewollt oder möglich ist. Dann muss der Anwender entscheiden, welche Eigenschaft ihm wichtiger ist: der mögliche Rückschluss auf die Grundgesamtheit (mit $\hat{\sigma}_{xy}$) oder die Interpretation als mittlere Abweichung von $(\bar{x},\bar{y})$ (mit s_xy).

Bei großen Stichprobenumfängen ist der Unterschied zwischen $\hat{\sigma}_{xy}$ und s_xy ohnehin klein, so dass die obige Überlegung nur bei kleinen Stichprobenumfängen angestellt werden muss.

Eigenschaften

Die folgende Eigenschaften gelten sowohl für die Stichprobenkovarianz als auch für die korrigierte Stichprobenkovarianz.

Interpretation der Kovarianz

• Die Kovarianz ist positiv, wenn X und Y tendenziell einen gleichsinnigen linearen Zusammenhang besitzen, d. h. hohe Werte von X gehen mit hohen Werten von Y einher und niedrige mit niedrigen.
• Die Kovarianz ist hingegen negativ, wenn X und Y einen gegensinnigen linearen Zusammenhang aufweisen, d. h. hohe Werte der einen Variablen gehen mit niedrigen Werten der anderen Variablen einher.
• Ist das Ergebnis 0, so besteht kein linearer Zusammenhang zwischen den beiden Variablen X und Y (nichtlineare Beziehungen sind möglich).

Die Kovarianz gibt zwar die Richtung eines Zusammenhangs zwischen zwei Variablen an, über die Stärke des Zusammenhangs kann aber, aufgrund der Linearität der Kovarianz, keine Aussage getroffen werden. Um einen Zusammenhang vergleichbar zu machen, muss die Kovarianz normiert werden. Die gebräuchlichste Normierung mittels der Standardabweichung führt zum Korrelationskoeffizienten.

Beziehung zur Varianz

Die Kovarianz ist eine Erweiterung der Varianz, denn es gilt

• s'² = s_xx bzw.
• $s^2=\hat{\sigma}_{xx}$.

Dabei ist s'² die Stichprobenvarianz und s² die korrigierte Stichprobenvarianz. Das heißt, die Varianz ist die Kovarianz einer Variable mit sich selbst.

Verschiebungssatz

Der Verschiebungssatz liefert eine alternative Darstellung der Kovarianz

• $s_{xy}=\frac{1}{n} \left( \sum_{i=1}^n {(x_i y_i) - n\bar{x}\bar{y}} \right)$
• $\hat{\sigma}_{xy} = \frac{1}{n-1} \left( \sum_{i=1}^n {(x_i y_i) - n\bar{x}\bar{y}} \right)$

. Diese Formeln ermöglichen in vielen Fällen eine einfachere Berechnung der Kovarianz. Bei numerischer Rechnung muss dabei allerdings auf unerwünschte Stellenauslösung bei der Subtraktion großer Zahlen geachtet werden.

Symmetrie und Linearität

Die Kovarianz ist linear und symmetrisch, d. h. es gilt:

Symmetrie

Beim Vertauschen der Rollen von x_i und y_i ergibt sich der gleiche Wert für die Kovarianz:

• s_xy = s_xy bzw.
• $\hat{\sigma}_{xy}=\hat{\sigma}_{yx}$

Linearität

Wird eine der Variablen einer linearen Transformation unterzogen, z.B. u_i = a + b * x_i, so gilt

• s_uy = bs_xy bzw.
• $\hat{\sigma}_{uy}=b\hat{\sigma}_{yx}$

Wegen der Symmetrie ist die Kovarianz auch im zweiten Argument linear.

Die Linearität der Kovarianz hat zur Folge, dass die Kovarianz vom Maßeinheit der Variablen abhängt. So erhält man beispielsweise die zehnfache Kovarianz, wenn man anstatt X die Variable 10X betrachtet. Da diese Eigenschaft die absoluten Werte der Kovarianz schwer interpretierbar macht, betrachtet man häufig stattdessen den maßstabsunabhängigen Korrelationskoeffizienten.

Beispiel

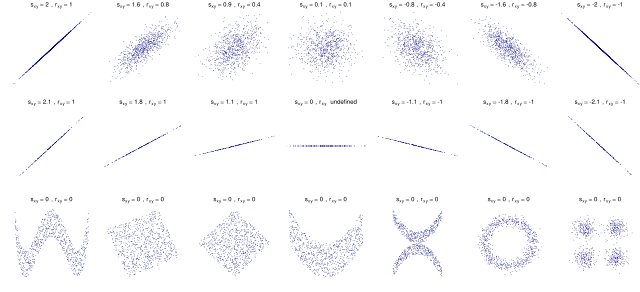
Die folgende Grafik zeigt für 21 verschiedene Datensätze jeweils das Streudiagramm zusammen mit der Kovarianz s_xy und der Korrelation r_xy des Datensatzes. Die erste Reihe zeigt sieben Datensätze mit unterschiedlich starkem linearen Zusammenhang, wobei die Korrelation r_xy von +1 über 0 nach minus eines geht. Da die Kovarianz ein nicht-standardisiertes Maß ist, geht sie von +2 auf Null bis auf -2. D.h., wenn es keinen linearen Zusammenhang gibt, dann ist die Kovarianz genauso Null wie die Korrelation. Das Vorzeichen der Kovarianz zeigt die Richtung des Zusammenhangs an; jedoch zeigt sie nicht die Stärke des Zusammenhangs.

Noch deutlicher wird es in der zweiten Zeile, wo alle sieben Datensätzen einen perfekten linearen Zusammenhang haben. Doch die Kovarianz s_xy nimmt ab auf Null und wird dann negativ. Die Korrelation r_xy ist für diese Datensätze entweder +1 oder -1 (bzw. undefiniert). Die dritte Zeile zeigt schließlich, dass sowohl die Kovarianz als auch die Korrelation Null ist, obwohl ein deutlicher Zusammenhang zwischen beiden Variablen sichtbar ist. D.h. die Kovarianz misst nur den linearen Zusammenhang und nicht-lineare Zusammenhänge werden nicht erkannt.

Siehe auch

• Kovarianzmatrix,
• Varianz
• Zusammenhangsmaß
• Korrelationskoeffizient